خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توزیع چند جمله ای ها (Distributing Polynomials)

در بخش های قبلی این فصل، چگونگی توزیع یک جمله روی چندین جمله را دیدید. در این بخش چگونگی توزیع یک دو جمله ای (binomial) - یک دوجمله ای، یک چند جمله ای (polynomial) است که دو جمله دارد - را خواهید دید. همچنین چگونگی توزیع یک چند جمله ای (polynomials) با سه جمله یا بیشتر را خواهید دید.

توزیع دو جمله روی چندین جمله فقط بکار بردن مراحل توزیع را به دوبار افزایش می دهد. در ادامه مراحل چگونگی توزیع یک دوجمله ای روی چندجمله ای ها را می بنید:
مثال: این عبارت را توزیع کنید:
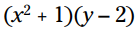
حالا که دانش این کار را پیدا کردید، یک توزیع چندجمله ای که در تمامی جملاتش متغیر دارد را امتحان کنید.
مثال: این توزیع را انجام بدهید:
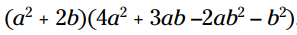
دوجمله ای را به جملات تشکیل دهنده اش بشکنید، و هر کدام از آن دو جمله را در فاکتور دوم ضرب کنید:
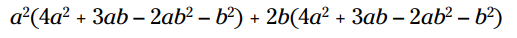
توزیع را انجام بدهید:
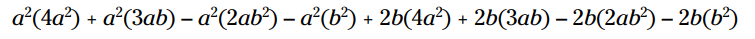
ضرب کنید و ساده کنید:
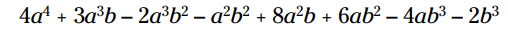
یک سه جمله ای (trinomial) - یک چندجمله ای (polynomial) که دارای سه جمله می باشد - می تواند روی عبارت دیگری توزیع شود. هر جمله در فاکتور اول به صورت جداگانه بر روی فاکتور دوم توزیع می شود، و سپس کل عبارت ساده می شود، هر چیزی که قابل ترکیب باشد، ترکیب می گردد. این فرآیند می تواند به توزیع هر چندجمله ای دیگر با هر تعداد جمله نیز تعمیم داده شود. در این بخش، من سه جمله ای ها را به شما نشان می دهم و تعمیم آن به چندجمله ای های بیش از سه جمله را به خودتان واگذار می کنم.
مسأله زیر مراحل توزیع سه جمله ای ها را به شما معرفی می کند.
مثال: ضرب را با توزیع فاکتور اول بر روی فاکتور دوم انجام بدهید:
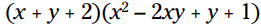
هر جمله از سه جمله ای را با ضرب کردن آن در فاکتور دوم، توزیع کنید:
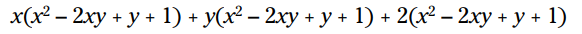
این سه توزیع را انجام بدهید:
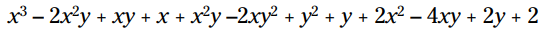
عبارت را ساده کنید:
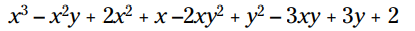
در اینجا می خواهم قانونی را بیان کنم که تقریباً می تواند هر ضربی با هر تعداد جمله را پوشش بدهد. شما می توانید از این روش کلی برای چهارجمله ای ها، پنج جمله ای ها، و حتی تعداد بیشتر جمله، استفاه نمایید.
مثال: این دو سه جمله ای را با توزیع در یکدیگر ضرب کنید:
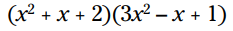
جملات فاکتور اول را از یکدیگر جدا کنید. هر جمله در فاکتور اول را در فاکتور دوم ضرب کنید:
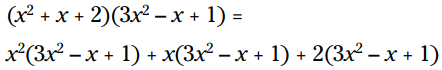
توزیع کنید و ضرب ها را انجام بدهید:
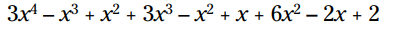
جملات مشابه را با یکدیگر ترکیب کنید:
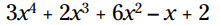

نکات فنی: کلمه polynomial از دو قسمت poly به معنای "چندین" و nomen به معنای "نام" یا "اسم" تشکیل شده است. یک polynomial یک عبارت جبری است که یک یا بیشتر جمله دارد. برای مثال، یک polynomial با یک جمله monomial (تک جمله ای)، یک polynomial با دو جمله binomial (دو جمله ای)، و یک polynomial با سه جمله trinomial (سه جمله ای) نامیده می شوند.
توزیع دوجمله ای ها (Distributing binomials)
توزیع دو جمله روی چندین جمله فقط بکار بردن مراحل توزیع را به دوبار افزایش می دهد. در ادامه مراحل چگونگی توزیع یک دوجمله ای روی چندجمله ای ها را می بنید:
-
دوجمله ای را به دو جمله تشکیل دهنده آن بشکنید.
-
هر کدام از جمله های دو جمله ای را روی سایر فاکتورها توزیع کنید.
-
توزیع ایجاد شده را انجام بدهید.
-
جملات مشابه را ترکیب نمایید و عبارت را ساده کنید.
مثال: این عبارت را توزیع کنید:
-
دوجمله ای را به دو جمله تشکیل دهنده آن بشکنید.
در این مورد، دوجمله ای اول را به دو جمله تشکیل دهندۀ آن یعنی x2 و 1 بشکنید.
-
هر کدام از جمله های دو جمله ای را روی سایر فاکتورها توزیع کنید.
جمله اول یعنی x2 را در دوجمله ای دوم ضرب کنید، و جمله دوم یعنی 1 را نیز در دوجمله ای دوم ضرب کنید.
-
توزیع ایجاد شده را انجام بدهید.
-
جملات مشابه را ترکیب نمایید و عبارت را ساده کنید.
در این مورد، هیچ چیزی نمی تواند ترکیب شود، هیچ کدام از جملات مشابه نمی باشند.
حالا که دانش این کار را پیدا کردید، یک توزیع چندجمله ای که در تمامی جملاتش متغیر دارد را امتحان کنید.
مثال: این توزیع را انجام بدهید:
دوجمله ای را به جملات تشکیل دهنده اش بشکنید، و هر کدام از آن دو جمله را در فاکتور دوم ضرب کنید:
توزیع را انجام بدهید:
ضرب کنید و ساده کنید:
توزیع سه جمله ای ها (Distributing trinomials)
یک سه جمله ای (trinomial) - یک چندجمله ای (polynomial) که دارای سه جمله می باشد - می تواند روی عبارت دیگری توزیع شود. هر جمله در فاکتور اول به صورت جداگانه بر روی فاکتور دوم توزیع می شود، و سپس کل عبارت ساده می شود، هر چیزی که قابل ترکیب باشد، ترکیب می گردد. این فرآیند می تواند به توزیع هر چندجمله ای دیگر با هر تعداد جمله نیز تعمیم داده شود. در این بخش، من سه جمله ای ها را به شما نشان می دهم و تعمیم آن به چندجمله ای های بیش از سه جمله را به خودتان واگذار می کنم.
مسأله زیر مراحل توزیع سه جمله ای ها را به شما معرفی می کند.
مثال: ضرب را با توزیع فاکتور اول بر روی فاکتور دوم انجام بدهید:
هر جمله از سه جمله ای را با ضرب کردن آن در فاکتور دوم، توزیع کنید:
این سه توزیع را انجام بدهید:
عبارت را ساده کنید:
ضرب کردن یک چندجمله ای در یک چندجمله ای دیگر
در اینجا می خواهم قانونی را بیان کنم که تقریباً می تواند هر ضربی با هر تعداد جمله را پوشش بدهد. شما می توانید از این روش کلی برای چهارجمله ای ها، پنج جمله ای ها، و حتی تعداد بیشتر جمله، استفاه نمایید.
قوانین جبر: هنگامی که یک چندجمله ای (polynomial) را روی یک چندجمله ای دیگر توزیع می کنید، هر جمله در فاکتور اول را در هر جمله از فاکتور دوم ضرب کنید. وقتی توزیع تمام شد، جملات مشابه را ترکیب کنید و عبارت را ساده کنید.
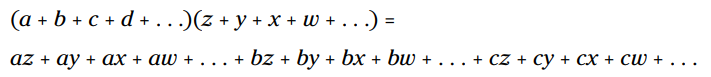
مثال: این دو سه جمله ای را با توزیع در یکدیگر ضرب کنید:
جملات فاکتور اول را از یکدیگر جدا کنید. هر جمله در فاکتور اول را در فاکتور دوم ضرب کنید:
توزیع کنید و ضرب ها را انجام بدهید:
جملات مشابه را با یکدیگر ترکیب کنید:
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (3 دیدگاه)
دیدگاه خود را ثبت کنید: