خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توزیع های خاص (اتحادها) (Special Distributions)

چند میانبر در توزیع می توانند زندگی را آسان تر کنند. توزیع دوجمله ای ها (binomials) بر روی چندجمله ای ها کار مشکلی نمی باشد، اما اگر بتوانید وضعیتهایی را که می توانید در آنها میانبرها را به کار گیرید، شناسایی کنید، منجر به صرفه جویی در زمانتان می گردد. اگر متوجه نشدید که یک میانبر خاص می توانست مورد استفاده قرار بگیرد، در مورد اشتباهتان زیاد نگران نباشید. اما اگر بعد از حل مسأله متوجه شدید راه آسانتری هم بوده است از ناراحتی موهای خودتان را نکنید!

مثال: مربع این دوجمله ای را با قوانین خاص بدست آورید:
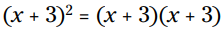
نتیجه این عملیات مجموع مربع x و مربع 3 همراه با دوبرابر حاصلضرب آنها می باشد:
بنابراین:

توجه کنید که ترتیب ترجیح داده شده از جملات مورد استفاده قرار گرفته اند: بر اساس کاهش توان x.
مثال: مربع این دوجمله ای را بر اساس قوانین خاص، بدست آورید:
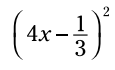
بنابراین:
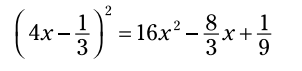
زمانیکه جملات دارای توان بالایی باشند، این قانون به خوبی کار می کند.
مثال: مربع این دوجمله ای را با قوانین خاص بدست آورید:
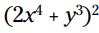
بنابراین:
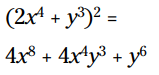
این روش خاص در مواقعیکه دوجمله ای شما خودش شامل دوجمله ای دیگری باشد نیز مفید ست!
مثال: مربع این عبارت را با قوانین خاص بدست آورید:
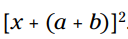
با کنار هم قرار دادن تمام نتایج خواهید داشت:
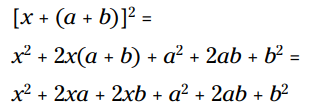
بین ضرب موجود در این بخش و بخش قبلی فقط یک تفاوت کوچک وجود دارد (که البته می تواند تفاوت بزرگی باشد!). تفاوت اینست که بین دوجمله ای اول ودوجمله ای دوم علامت تغییر می کند. در این بخش، به جای اینکه یک دوجمله ای را دقیقاً در خودش ضرب کنید، در جمله دوم یک تغییر علامت می دهید. این دو فاکتور صرفنظر از تفاوت در علامتشان، کاملاً یکسان خواهند بود.
تشخیص مجموع دو جمله که در تفاضل بین همان دو جمله یکسان ضرب شده اند ساده می باشد و حتی کار کردن با آن از تشخیص دادنش هم ساده تر می باشد.
توجه کنید که جمله میانی ناپدید می شود زیرا یک جمله و متضاد آن همیشه در وسط قرار می گیرند. در اینجا می توانید چگونگی توزیع جملات دوجمله ای اول روی دومی را ببینید:
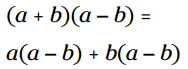
ضرب ها را انجام داده و ساده کنید:
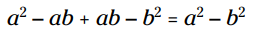
این قانون همیشه کار می کند، بنابراین شما می توانید از این میانبر برای انجام این توزیع های خاص استفاده کنید.
مثال: با قوانین خاص حاصلضرب این دو را پیدا کنید:
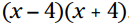
بنابراین:
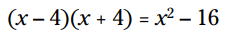
مثال: با قانون خاص حاصلضرب را بدست آورید: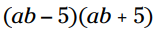
در این مسأله متغیر جمله اندکی پیچیده تر است.
بنابراین:
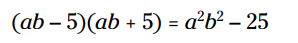
مثال: با قانون خاص حاصلضرب را پیدا کنید: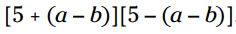 .
.
در این مسأله جمله دوم یک دوجمله ای می باشد.
مربع دوجمله ای را بدست آورید و علامت منفی را توزیع کنید:
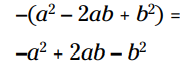
بنابراین:
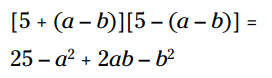
خوب، اول ببینیم مکعب (cubes) چیست؟ مکعب در ریاضی چند معنا دارد. برخی مکعب ها اشیاء سه بعدی هستند، اما آن مکعبی که در این بخش مدنظر است مقادیری هستند که سه مرتبه در خودشان ضرب شده اند. در واقع به توان 3 رسیده اند.
معمولاً شناسایی یک مسأله ضرب که در نهایت نتیجه اش تفاضل یا مجموع دو مکعب گردد، بسیار دشوار می باشد. شما ممکن است متوجه نشوید که چنین پاسخ ساده ای در انتظار شما می باشد تا اینکه به انتهای مسأله می رسید و خواهید گفت: "اوه، آره. از اون نوعش بود!". با این وجود، شناسایی اینکه نتیجه مسأله تفاضل یا مجموع دو مکعب می شود، در ادامه و در فصل 14 که در آن به معادلات مکعبی (cubic equations) - معادلاتی که شامل یک جمله با توان 3 و نه بیشتر می باشند - می پردازیم، مهمتر هم می شود.
برای شناسایی اینکه چه نوع از مسأله های ضرب نتیجه شان تفاضل یا مجموع دو مکعب می باشند، بررسی کنید که آیا توزیع شامل یک دوجمله ای ضربدر یک سه جمله ای می باشد. دوجمله ای شامل دو ریشه مکعب می باشد، و سه جمله ای شامل مربع دو ریشه و متضاد حاصلضرب دو ریشه می باشد.
اجازه بدهید توزیع را به شما نشان بدهم تا اثبات شود چرا این الگو درست کار می کند:
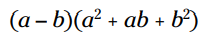
a و b- را در سه جمله ای توزیع کنید:
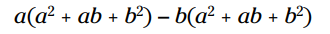
دو مقدار را به صورت جداگانه توزیع کنید و جملات را در یکدیگر ضرب کنید:
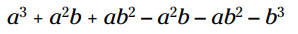
توجه کنید که چهار جمله میانی همگی جفت های معکوس یکدیگر هستند و حاصلجمع آنها 0 می شود:
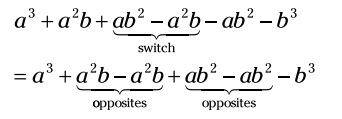
در نهایت آنچه که برای شما باقی می ماند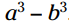 می باشد.
می باشد.
نتیجه این الگو همواره تفاضل بین دو مکعب می باشد.
مثال: با استفاده از قوانین خاص و الگوها، این ضرب را انجام دهید:
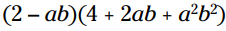
این ضرب با الگو مطابقت دارد، زیرا مربع اولین جمله در دوجمله ای برابر با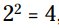 است، و مربع دومین جمله برابر با
است، و مربع دومین جمله برابر با 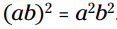 است. متضاد حاصلضرب دو جمله در دوجمله ای برابر با
است. متضاد حاصلضرب دو جمله در دوجمله ای برابر با 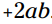 می باشد. این سه جمله ای دقیقاً آنچیزی است که باید باشد. بنابراین طبق الگو حاصلضرب آنها باید بشود مکعب دو عدد موجود در دوجمله ای. مکعب 2 می شود 8 و مکعب ab- می شود
می باشد. این سه جمله ای دقیقاً آنچیزی است که باید باشد. بنابراین طبق الگو حاصلضرب آنها باید بشود مکعب دو عدد موجود در دوجمله ای. مکعب 2 می شود 8 و مکعب ab- می شود 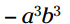 .
.
بنابراین:
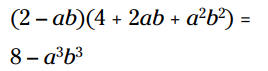
مثال: با قانون خاص و الگو این ضرب را انجام بدهید:
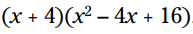
این ضرب همه چیزهای مناسب را دارد. از آنجا که علامت موجود در دوجمله ای + می باشد، پس علامت پاسخ نیز + می باشد. مکعب 4 می شود 64 . بنابراین:
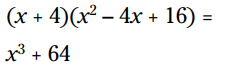
مثال: با قانون خاص و الگو این ضرب را انجام بدهید:
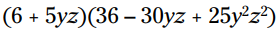
این مسأله کاملاً واضح نیست. شما باید تشخیص بدهید متضاد حاصلضرب دو جمله در دوجمله ای می شود 30yz- . اما هنگامی که الگو را درک کردید، کافیست مکعب 6 را پیدا کنید که می شود 216 و مکعب 5yz که برابر با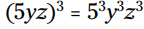 می باشد. بنابراین:
می باشد. بنابراین:
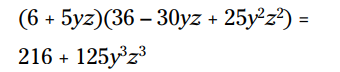

یادداشت مترجم: توزیع های خاص (Special Distributions)، در آموزش ریاضی در مدارس ایران با نام اتحادها شناسایی می شوند.
مربع دو جملهای (اتحاد اول و اتحاد دوم)
قوانین جبر: هنگامی که یک دوجمله ای در خودش ضرب شود - یعنی هر کدام از دو جمله اول در عبارت یکسان دوم توزیع گردد - سپس حاصلضرب یک سه جمله ای می شود که شامل مربع دو جمله و دوبرابر حاصلضرب آنها می باشد:
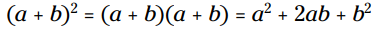
یادداشت مترجم: در اینجا نویسندۀ کتاب قانون مربع دوجمله ای را به شکلی بیان کرده است که معادل آموزش ریاضی آن در مدارس ایران یعنی اتحاد اول و اتحاد دوم را با یک قانون پوشش داده است. به منظور یادآوری و همینطور مقایسه جهت درک بهتر مطلب، این دو اتحاد را در اینجا ذکر می کنم:
اتحاد اول (مربع مجموع دو جملهای):
اتحاد دوم (مربع تفاضل دو جملهای):
اتحاد اول (مربع مجموع دو جملهای):
(a + b)2 = a2 + 2ab + b2
اتحاد دوم (مربع تفاضل دو جملهای):
(a - b)2 = a2 - 2ab + b2
مثال: مربع این دوجمله ای را با قوانین خاص بدست آورید:
نتیجه این عملیات مجموع مربع x و مربع 3 همراه با دوبرابر حاصلضرب آنها می باشد:
-
مربع x می شود x2 .
-
مربع 3 می شود 9 .
-
دوبرابر حاصلضرب x و 3 می شود
.
بنابراین:
توجه کنید که ترتیب ترجیح داده شده از جملات مورد استفاده قرار گرفته اند: بر اساس کاهش توان x.
مثال: مربع این دوجمله ای را بر اساس قوانین خاص، بدست آورید:
-
مربع 4x می شود
.
-
مربع 1/3- می شود
.
-
دوبرابر حاصلضرب 4x در 1/3- می شود
.
بنابراین:
زمانیکه جملات دارای توان بالایی باشند، این قانون به خوبی کار می کند.
مثال: مربع این دوجمله ای را با قوانین خاص بدست آورید:
-
مربع 2x4 می شود
.
-
مربع y3 می شود
.
-
دوبرابر حاصلضرب 2x4 و y3 می شود
.
بنابراین:
این روش خاص در مواقعیکه دوجمله ای شما خودش شامل دوجمله ای دیگری باشد نیز مفید ست!
مثال: مربع این عبارت را با قوانین خاص بدست آورید:
-
مربع x می شود
.
-
مربع دوجمله ای (a + b) می شود
.
-
دوبرابر حاصلضرب x و (a + b) می شود
.
با کنار هم قرار دادن تمام نتایج خواهید داشت:
اتحاد مزدوج
بین ضرب موجود در این بخش و بخش قبلی فقط یک تفاوت کوچک وجود دارد (که البته می تواند تفاوت بزرگی باشد!). تفاوت اینست که بین دوجمله ای اول ودوجمله ای دوم علامت تغییر می کند. در این بخش، به جای اینکه یک دوجمله ای را دقیقاً در خودش ضرب کنید، در جمله دوم یک تغییر علامت می دهید. این دو فاکتور صرفنظر از تفاوت در علامتشان، کاملاً یکسان خواهند بود.
تشخیص مجموع دو جمله که در تفاضل بین همان دو جمله یکسان ضرب شده اند ساده می باشد و حتی کار کردن با آن از تشخیص دادنش هم ساده تر می باشد.
قوانین جبر: مجموع هر دو جمله که در اختلاف همان دو جمله ضرب شده اند برابر با تفاضل مربع هر کدام از جمله ها می باشد. برای هر عدد حقیقی a و b داریم:
(a + b)(a - b) = a2 - b2
توجه کنید که جمله میانی ناپدید می شود زیرا یک جمله و متضاد آن همیشه در وسط قرار می گیرند. در اینجا می توانید چگونگی توزیع جملات دوجمله ای اول روی دومی را ببینید:
ضرب ها را انجام داده و ساده کنید:
این قانون همیشه کار می کند، بنابراین شما می توانید از این میانبر برای انجام این توزیع های خاص استفاده کنید.
مثال: با قوانین خاص حاصلضرب این دو را پیدا کنید:
-
مربع جمله اول x2 می شود.
-
جمله دوم همیشه منفی خواهد بود و مثل جمله اول یک مربع کامل می باشد:
بنابراین:
مثال: با قانون خاص حاصلضرب را بدست آورید:
در این مسأله متغیر جمله اندکی پیچیده تر است.
-
مربع ab می شود
.
-
متضاد مربع 5 می شود 25- .
بنابراین:
مثال: با قانون خاص حاصلضرب را پیدا کنید:
در این مسأله جمله دوم یک دوجمله ای می باشد.
-
مربع 5 می شود 25 .
-
متضاد مربع (a - b) می شود
.
مربع دوجمله ای را بدست آورید و علامت منفی را توزیع کنید:
بنابراین:
مجموع و تفاضل مکعبات دوجمله (اتحاد چاق و لاغر یا فیل و فنجان)
خوب، اول ببینیم مکعب (cubes) چیست؟ مکعب در ریاضی چند معنا دارد. برخی مکعب ها اشیاء سه بعدی هستند، اما آن مکعبی که در این بخش مدنظر است مقادیری هستند که سه مرتبه در خودشان ضرب شده اند. در واقع به توان 3 رسیده اند.
یادتان باشد: یک مقدار که در خودش ضرب شده باشد یک مربع کامل (perfect square) می باشد. مقداری که سه مرتبه در خودش ضرب شده باشد یک مکعب کامل (perfect cube) می باشد. بنابراین، مقدار 33 برابر با 27 می باشد، زیرا 27 = 3 . 3 . 3، مکعب متغیر x برابر با x3 است.
معمولاً شناسایی یک مسأله ضرب که در نهایت نتیجه اش تفاضل یا مجموع دو مکعب گردد، بسیار دشوار می باشد. شما ممکن است متوجه نشوید که چنین پاسخ ساده ای در انتظار شما می باشد تا اینکه به انتهای مسأله می رسید و خواهید گفت: "اوه، آره. از اون نوعش بود!". با این وجود، شناسایی اینکه نتیجه مسأله تفاضل یا مجموع دو مکعب می شود، در ادامه و در فصل 14 که در آن به معادلات مکعبی (cubic equations) - معادلاتی که شامل یک جمله با توان 3 و نه بیشتر می باشند - می پردازیم، مهمتر هم می شود.
قوانین جبر: تفاضل یا مجموع دو مکعب برابر می باشد با تفاضل یا مجموع ریشه آن دو مکعب ضربدر یک سه جمله ای که شامل مربع ریشه مکعب ها و متضاد حاصلضرب ریشه های مکعب می باشد. برای هر عدد حقیقی a و b داریم:
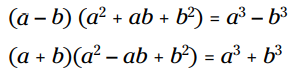
برای شناسایی اینکه چه نوع از مسأله های ضرب نتیجه شان تفاضل یا مجموع دو مکعب می باشند، بررسی کنید که آیا توزیع شامل یک دوجمله ای ضربدر یک سه جمله ای می باشد. دوجمله ای شامل دو ریشه مکعب می باشد، و سه جمله ای شامل مربع دو ریشه و متضاد حاصلضرب دو ریشه می باشد.
یادتان باشد: متضاد یک عدد، همان عدد با علامتی متفاوت در مقابلش می باشد. اگر عدد مربوطه منفی باشد، پس متضادش مثبت می شود و برعکس.
اجازه بدهید توزیع را به شما نشان بدهم تا اثبات شود چرا این الگو درست کار می کند:
a و b- را در سه جمله ای توزیع کنید:
دو مقدار را به صورت جداگانه توزیع کنید و جملات را در یکدیگر ضرب کنید:
توجه کنید که چهار جمله میانی همگی جفت های معکوس یکدیگر هستند و حاصلجمع آنها 0 می شود:
در نهایت آنچه که برای شما باقی می ماند
نتیجه این الگو همواره تفاضل بین دو مکعب می باشد.
مثال: با استفاده از قوانین خاص و الگوها، این ضرب را انجام دهید:
این ضرب با الگو مطابقت دارد، زیرا مربع اولین جمله در دوجمله ای برابر با
بنابراین:
مثال: با قانون خاص و الگو این ضرب را انجام بدهید:
این ضرب همه چیزهای مناسب را دارد. از آنجا که علامت موجود در دوجمله ای + می باشد، پس علامت پاسخ نیز + می باشد. مکعب 4 می شود 64 . بنابراین:
مثال: با قانون خاص و الگو این ضرب را انجام بدهید:
این مسأله کاملاً واضح نیست. شما باید تشخیص بدهید متضاد حاصلضرب دو جمله در دوجمله ای می شود 30yz- . اما هنگامی که الگو را درک کردید، کافیست مکعب 6 را پیدا کنید که می شود 216 و مکعب 5yz که برابر با
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (4 دیدگاه)
دیدگاه خود را ثبت کنید: