خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
انتخاب گزینه های فاکتورگیری

گاهی اوقات مجبور می شوید یک مسأله را بیش از یکبار فاکتورگیری کنید. این بخش به شما نشان می دهد چگونه می توانید دو تکنیک کاملاً متفاوت فاکتورگیری را روی یک مسأله استفاده کنید. فرآیند استفاده از تکنیکهای مختلف فاکتورگیری، متفاوت از استفاده مجدد از یک روش یکسان، همچون بیرون کشیدن چندبارۀ فاکتورهای مشترک، می باشد.

یک عبارت درجه دوم، همچون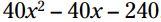 ، می تواند توسط دو تکنیک مختلف، که می توانند در دو ترتیب مختلف انجام شوند، فاکتورگیری شود. یکی از انتخابها مسأله را ساده تر می کند. آن ترتیبی است که در آن فاکتورگیری انجام می شود و یک روش را ساده تر و روش دیگر را سختتر می کند. شما باید فقط امیدوار باشید قبل از شروع روش ساده تر را شناسایی کنید.
، می تواند توسط دو تکنیک مختلف، که می توانند در دو ترتیب مختلف انجام شوند، فاکتورگیری شود. یکی از انتخابها مسأله را ساده تر می کند. آن ترتیبی است که در آن فاکتورگیری انجام می شود و یک روش را ساده تر و روش دیگر را سختتر می کند. شما باید فقط امیدوار باشید قبل از شروع روش ساده تر را شناسایی کنید.
من ابتدا روش سختتر را به شما نشان می دهم، بنابراین خواهید دید چرا مهم است که انتخاب خوبی داشته باشید. در این مورد، اعداد بزرگ نگهداشته می شوند و عملیات unFOIL ابتدا انجام می شود.
مثال: عبارت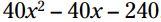 را با شیوه unFOIL در ابتدا، فاکتور گیری کنید.
را با شیوه unFOIL در ابتدا، فاکتور گیری کنید.
در اینجا دو نوع فاکتورگیری مورد استفاده قرار گرفتند: فاکتورگیری به روش unFOIL و فاکتورگیری به روش GCF (بزرگترین فاکتور مشترک).
در ادامه روش ساده تر را امتحان می کنیم.
مثال: عبارت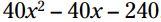 را با شیوه GCF در ابتدا، فاکتور گیری کنید.
را با شیوه GCF در ابتدا، فاکتور گیری کنید.
ضریب های هر جمله بر 40 بخش پذیر می باشد. فاکتورگیری را انجام بدهید:

حالا به سه جمله ای موجود در داخل پرانتز نگاه کنید:
با توجه به اینکه روش های فاکتورگیری بسیاری در جبر وجود دارد، تعجب آور نیست که در یک مسأله واحد، شما ترکیبهای مختلفی از فاکتورگیریهای متفاوت را پیدا کنید. در فصل 10، شما فاکتورگیری از مجموع و تفاضل مکعب ها و تفاضل مربع ها را خواهید دید. در حال حاضر، من به روشهایی می چسبم که در این فصل و فصل قبل از آن یعنی 8 مطرح کردیم، تا ترکیب جالب دیگری را به شما نشان بدهم.
در مثال بعدی، شما شش جمله را خواهید دید - یک نوع عبارت که به نظر می رسد پیشنهاد می شود از گروه بندی برای فاکتورگیری آن استفاده کنید. سورپرایز بزرگ بعد از اتمام گروه بندی خواهد بود.
مثال: این عبارت را فاکتورگیری کنید:
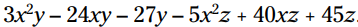
سه جمله اول دارای ضریبهایی می باشند که بر 3 بخش پذیرند، و هر کدام فاکتوری از y دارند. بنابراین 3y را از آنها فاکتور می گیریم. سه جمله آخر دارای ضریبهایی می باشند که بر 5 بخش پذیرند، و هر کدام فاکتوری از z دارند، بنابراین 5z را از هر سه جمله مربوطه فاکتور می گیریم.
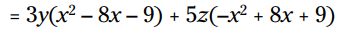
شما می توانید ببینید که دو سه جمله ای ما یکسان نمی باشند. برای اینکه گروه بندی کار کند، شما باید تعداد جملات کمتری را بسازید - هر کدام با فاکتورهایی مشترک. مشکل در اینجا اینست که من 5- را فاکتور نگرفته ام. بله، من متوجه مسأله شدم، اما می خواهم به شما نشان بدهم که جبران آن آسان است. کافیست 5z+ را به 5z- تغییر بدهم و 1- را از هر کدام از جملات موجود در سه جمله ای دوم فاکتور بگیرم. در واقع فاکتورگیری از 1- صرفاً تغییر دادن علامت جملات به متضاد آنها می باشد:
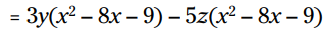
اکنون می توانم سه جمله ای را فاکتور بگیرم:

سه جمله ای ما می تواند با روش unFOIL به دو دوجمله ای تشکیل دهندۀ آن فاکتورگیری گردد. نتیجه نهایی را در ادامه می بینید:
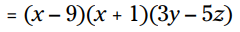

ترکیب unFOIL و بزرگترین فاکتور مشترک
یک عبارت درجه دوم، همچون
من ابتدا روش سختتر را به شما نشان می دهم، بنابراین خواهید دید چرا مهم است که انتخاب خوبی داشته باشید. در این مورد، اعداد بزرگ نگهداشته می شوند و عملیات unFOIL ابتدا انجام می شود.
مثال: عبارت
-
تمامی روش هایی را که می توان دو عدد را در یکدیگر ضرب کرد تا به 40 رسید، تعیین کنید.
40 = 40 × 1 = 20 × 2 = 10 × 4 = 8 × 5
-
تمامی روش هایی را که می توان دو عدد را در یکدیگر ضرب کرد تا به 240 رسید، تعیین کنید.
240 = 240 × 1 = 120 × 2 = 80 × 3 = 60 × 4 = 48 × 5 = 40 × 6 = 30 × 8 = 24 × 10 = 20 × 12 = 16 × 15
-
علامت جمله آخر، 240-، به شما می گوید که نیاز به یک تفاضل دارید. تفاضل حاصلضربها باید 40 گردد.
انتخابهای ما به شرح زیر می باشند:
10 × 4 and 20 × 12
حالا با من رو راست باشید. آیا پیدا کردن لیست مضربها و همینطور پیدا کردن ترکیب صحیح برای محاسبه تفاضل دو حاصلضرب کار چالش برانگیز و مشکلی بود؟ برای من که قطعاً اینطور بوده است!
(4)(20) = 80
(12)(10) = 120
120 - 80 = 40
-
انتخابهایتان را به شکل دوجمله ای ها سازماندهی کنید و علامتها را به درستی قرار بدهید.
اما نگاهی به ضریب های موجود در دوجمله ای ها بیندازید. هر جفت از دوجمله ای ها خودشان قابل فاکتورگیری هستند. هر کدام از جمله های موجود در دوجمله ای اول را می توانید با عدد 4 فاکتورگیری کنید، و هرکدام از جملات موجود در دوجمله ای دوم را نیز می توانید با 10 فاکتورگیری کنید.
در اینجا دو نوع فاکتورگیری مورد استفاده قرار گرفتند: فاکتورگیری به روش unFOIL و فاکتورگیری به روش GCF (بزرگترین فاکتور مشترک).
در ادامه روش ساده تر را امتحان می کنیم.
مثال: عبارت
ضریب های هر جمله بر 40 بخش پذیر می باشد. فاکتورگیری را انجام بدهید:
حالا به سه جمله ای موجود در داخل پرانتز نگاه کنید:
-
با استفاده از روش unFOIL سه جمله ای
را فاکتور بگیرید.
عدد 1 را می توان صرفاً به صورت حاصلضربنمابش داد. عدد 6 را هم می توان به صورت حاصلضرب
یا
نمایش داد. توجه کنید که چگونه لیست انتخابها کوتاهتر و قابل مدیریت تر از روش قبلی که در ابتدا unFOIL را انجام داده بودید، می شود.
-
به علامت آخرین جمله، 6-، نگاه کنید. حاصلضربهایی را انتخاب کنید که تفاضل آنها 1 گردد.
با استفاده از ترکیبو
ایجاد فاکتورها آسان می باشد:
عبارت میانی یعنی x، منفی می باشد، بنابراین شما نیاز به 3x دارید، حاصلضرب دو جمله بیرونی باید منفی باشند. فاکتورگیری را تکمیل کنید. سپس عدد 40 را که در ابتدا فاکتور گرفته بودید در ابتدای پاسخ قرار بدهید.
نکته: از هر کدام از این دو ترتیب که استفاده کنید در نهایت به پاسخ صحیح خواهید رسید. با این حال، به عنوان یک قانون کلی، اینکه ابتدا با استفاده از روش GCF فاکتورگیری کنید، بهتر است.
گروه بندی و استفاده از unFOIL در یک بسته بندی
با توجه به اینکه روش های فاکتورگیری بسیاری در جبر وجود دارد، تعجب آور نیست که در یک مسأله واحد، شما ترکیبهای مختلفی از فاکتورگیریهای متفاوت را پیدا کنید. در فصل 10، شما فاکتورگیری از مجموع و تفاضل مکعب ها و تفاضل مربع ها را خواهید دید. در حال حاضر، من به روشهایی می چسبم که در این فصل و فصل قبل از آن یعنی 8 مطرح کردیم، تا ترکیب جالب دیگری را به شما نشان بدهم.
در مثال بعدی، شما شش جمله را خواهید دید - یک نوع عبارت که به نظر می رسد پیشنهاد می شود از گروه بندی برای فاکتورگیری آن استفاده کنید. سورپرایز بزرگ بعد از اتمام گروه بندی خواهد بود.
مثال: این عبارت را فاکتورگیری کنید:
سه جمله اول دارای ضریبهایی می باشند که بر 3 بخش پذیرند، و هر کدام فاکتوری از y دارند. بنابراین 3y را از آنها فاکتور می گیریم. سه جمله آخر دارای ضریبهایی می باشند که بر 5 بخش پذیرند، و هر کدام فاکتوری از z دارند، بنابراین 5z را از هر سه جمله مربوطه فاکتور می گیریم.
شما می توانید ببینید که دو سه جمله ای ما یکسان نمی باشند. برای اینکه گروه بندی کار کند، شما باید تعداد جملات کمتری را بسازید - هر کدام با فاکتورهایی مشترک. مشکل در اینجا اینست که من 5- را فاکتور نگرفته ام. بله، من متوجه مسأله شدم، اما می خواهم به شما نشان بدهم که جبران آن آسان است. کافیست 5z+ را به 5z- تغییر بدهم و 1- را از هر کدام از جملات موجود در سه جمله ای دوم فاکتور بگیرم. در واقع فاکتورگیری از 1- صرفاً تغییر دادن علامت جملات به متضاد آنها می باشد:
اکنون می توانم سه جمله ای را فاکتور بگیرم:
سه جمله ای ما می تواند با روش unFOIL به دو دوجمله ای تشکیل دهندۀ آن فاکتورگیری گردد. نتیجه نهایی را در ادامه می بینید:
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: