در این فصل، شما ملاحظات بسیاری را که شامل حل کردن معادلات در جبر می شوند، خواهید دانست. در فصل های پیشین، مکانیک صحیح کار با عبارتهای جبری را پوشش دادم. اکنون با معرفی علامت برابری (=) آن قوانین را به کار می گیرم. درست مانند فعل که عبارت را به جمله تبدیل می کند، علامت برابری عبارت ریاضی را به معادله تبدیل می کند. در این فصل، به جای سر و کار داشتن با عباراتی همچون 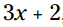به شما نشان می دهم چگونه برای حل کردن معادلاتی همچون 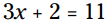آماده شوید.





معادلات دو جمله ای بسیار ساده هستند. در معادلات ساده تر استاد شوید، تا بتوانید تکنیکهایی را که در این معادلات مورد استفاده قرار می دهید در معادلات پیچیده تر بکار بگیرید. با استفاده از معادلات دارای بیش از دو جمله، یا تبدیل توانهای متغیرها به اعداد بزرگتر از 1، شما امکانات فراوانی را برای پاسخهای معادلات ساده خواهید داشت.

ایجاد سازماندهی صحیح برای حل معادلات

برای حل کردن پاسخ صحیح انواع مختلف معادلات، انواع رسیدگی های مختلف وجود دارند. سازماندهی معادله بستگی به این دارد که در آن زمان با چه نوع معادله ای سر و کار دارید.

در اینجا لیستی از رایج ترین انواع معادلات جبری و عمومی ترین شکل آنها را می بینید:

• معادله خطی (Linear equation):
  
  
• معادله درجه دوم (Quadratic equation):
  
  
• معادله مکعبی (Cubic equation):
  
  
• معادله چندجمله ای عمومی (General polynomial equation):
  
  
• معادله رادیکالی (Radical equation):
  
  
• معادله گویا (Rational equation):
  
  
• دستگاه معادلات خطی (System of linear equations):
  

به طور کلی، معمولاً معادلات را برابر با 0 یا برابر با برخی از ثابتها قرار می دهند. در مورد تفاوتها و شباهتهای این دو در فصلهای آینده جزئیات بیشتری را پوشش خواهم داد.