یک عدد موهومی (imaginary number) چیزی است که وجود ندارد - خوب، دست کم تا زمانیکه برخی از ریاضیدانان پرآوازه راه خودشان را انتخاب کردند. آنها از بابت اینکه در هنگام حل کردن معادلات به دلیل اینکه یک عدد منفی در زیر رادیکال قرار می گرفت و عملیات را متوقف می کرد، خوشحال نبودند. به همین دلیل با عدد موهومی i بر این مشکل فائق آمدند.





قوانین جبر: جذر 1- به عنوان i تعیین شده است.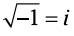 و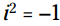

از وقتی که مقدار i اعلام شد، تمامی انواع ریاضیات شسته و رفته و برنامه های کاربردی ظاهر شدند. از بابت اینکه نمی توانم تمامی چیزهای خوب در این زمینه را در این کتاب پوشش بدهم متاسفم، اما دست کم یک پیش نمایش از آنچیزی که اعداد مختلط (complex numbers) در آن ارتباط هستند را به شما نشان می دهم.

در هنگام استفاده از فرمول حل کردن معادلات درجه دوم، این امکان وجود دارد که اعداد موهومی را تجربه کنید. در مثال بعدی، معادله درجه دوم، قابل فاکتورگیری نمی باشد و همچنین هیچ پاسخ حقیقی ندارد (تنها پاسخ ممکن اعداد موهومی می باشند).

مثال: با استفاده از فرمول معادلات درجه دوم، این معادله را حل کنید: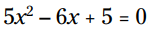

در این معادله درجه دوم، a = 5 و b = -6 و c = 5 هستند. با قرار دادن این اعداد در فرمول حل معادلات درجه دوم، خواهیم داشت:


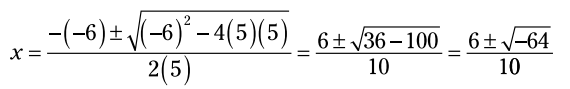
شما یک 64- را در زیر رادیکال می بینید. تنها اعداد مثبت و 0 دارای جذر هستند. بنابراین شما از تعریف عدد موهومی که می گوید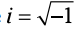 استفاده می کنید و بعد از ساده سازی رادیکال اعمال می کنید:


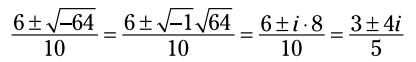
به کار بردن این عدد موهومی جدید به ریاضیدانان امکان می دهد تا مسأله های خودشان را به پایان برسانند. شما در اینجا دو پاسخ دارید - اگرچه هر دوی آن پاسخها موهومی (خیالی) هستند. (درست مانند آن دوست خیالی تان می ماند که در دوران کودکی همراه شما بود!)