خطوط موازی (Parallel) و خطوط عمود بر یکدیگر (Perpendicular)

شیب یک خط (slope of a line) اطلاعاتی در مورد ویژگی های خاص آن خط را به شما می دهد. شیب خط به شما می گوید که آیا آن خط تند است یا مسطح و در صورتی که جهت خط را از چپ به راست در نظر بگیریم آیا آن خط رو به سمت بالا می رود یا رو به سمت پایین می رود. همچنین شیب خط می تواند به شما بگوید که آیا خطی بر خط دیگر موازی یا عمود می باشد یا خیر. شکل 9-20 خطوط موازی و خطوط عمود بر یکدیگر را به شما نشان می دهد.

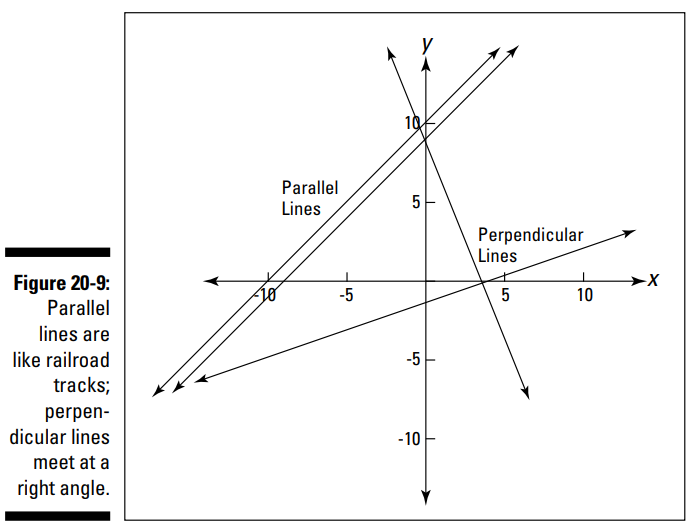
خطوط موازی (Parallel lines) هرگز به همدیگر نمی رسند. آنها همیشه با فاصله یکسانی جدا از یکدیگر قرار دارند و هرگز نقطه ای را با یکدیگر به اشتراک نمی گذارند. شیب (slope) آنها با هم برابر است.

خطوط عمود بر یکدیگر (Perpendicular lines) در جایی که یکدیگر را قطع می کنند، یک زاویه \(90^\circ\) یا زاویۀ قائمه را با هم تشکیل می دهند. آنها دارای شیب هایی هستند که معکوس منفی یکدیگر می باشند. محورهای \(x\) و \(y\) خطوط عمود بر یکدیگر می باشند.

یادتان باشد: اگر حاصلضرب دو عدد \(1\) شود، آن دو عدد معکوس یکدیگر (reciprocals) می باشند. اعداد \({3\over4}\) و \({4\over3}\) معکوس یکدیگر می باشند. اگر حاصلضرب دو عدد \(-1\) گردد، آن دو عدد معکوس منفی یکدیگر (negative reciprocals) می باشند. اعداد \({3\over4}\) و \(-{4\over3}\) معکوس منفی یکدیگر می باشند.

قوانین جبر: اگر خط \(y_1\) دارای شیب \(m_1\) ، و خط \(y_2\) دارای شیب \(m_2\) باشد، سپس اگر \(m_1 = m_2\) باشد، این دو خط با هم موازی هستند. اگر خط \(y_1\) دارای شیب \(m_1\) و خط \(y_2\) دارای شیب \(m_2\) باشند، و اگر \(m_1=-{1 \over m_2}\) باشد، سپس این دو خط بر یکدیگر عمود می باشند.

مثالهای زیر به شما نشان می دهند چگونه صرفاً با نگاه کردن به شیب خطها می توانید تشخیص بدهید که آیا آنها با یکدیگر موازی هستند یا بر یکدیگر عمودند:

خط \(y=3x+2\) با خط \(y=3x-7\) موازی می باشند، زیرا شیب هر دوی آنها \(3\) می باشد.
خط \(y={-1\over4}x+3\) با خط \(y={-1\over4}x+1\) موازی می باشند، زیرا شیب هردوی آنها \(y={-1\over4}\) است.
خط \(3x+2y=8\) و خط \(6x+4y=7\) با یکدیگر موازی می باشند، زیرا شیب هر دوی آنها \({-3\over2}\) می باشد. برای بدست آوردن شیب خط لازم است تا این معادلات را در شکل شیب-تقاطع (slope-intercept) بنویسید: \(3x+2y=8\) می تواند به شکل \(y={-3 \over 2}x+4\) نوشته شود و \(6x+4y=7\) می تواند به شکل \(y={-3 \over 2}x+{7\over4}\) نوشته شود.
خط \(y={3\over4}x+5\) بر خط \(y={-4\over3}x+6\) عمود می باشد، زیرا شیب آنها معکوس منفی یکدیگر می باشند.
خط \(y=-3x+4\) بر خط \(y={1\over3}x-8\) عمود می باشد، زیرا شیب آنها معکوس منفی یکدیگر می باشند.