خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
خطوط متقاطع (Intersecting Lines)
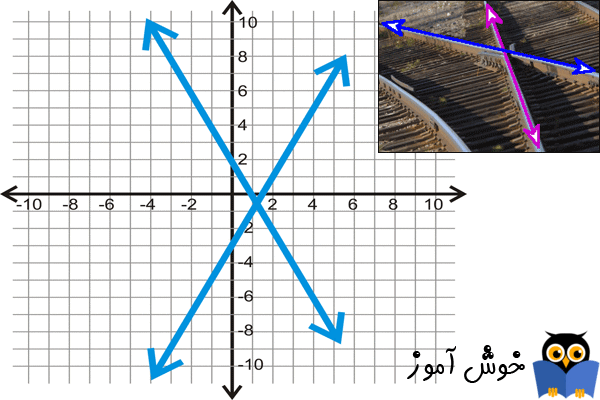
اگر دو خط متقاطع (intersect) باشند، یعنی از یکدیگر عبور کرده باشند، سپس محل تقاطع آنها دقیقاً یک و فقط یک نقطه می باشد. محلی که خطوط از یکدیگر عبور کرده اند محل تقاطع آنها می باشد و این نقطه مشترک، تنها نقطه ای است که هر دوی این خطوط آن را به اشتراک گذارده اند. ترسیم با دقت نمودارها گاهی اوقات می تواند در پیدا کردن نقطه تقاطع به شما کمک کند.

نقطۀ \((5,1)\) نقطه تقاطع بین دو خط \(x+y=6\) و \(2x-y=9\) می باشد، زیرا این مختصات هر دو معادله را برقرار می سازد:
این نقطه، تنها مختصاتی می باشد که بر روی هر دو خط قرار دارد.
ترسیم با دقت نمودار می تواند محل تقاطع دو خط را به شما بدهد. تنها مشکل اینست که اگر نمودار شما حتی اندکی غیردقیق باشد، ممکن است پاسخ اشتباهی را بدست آورید. همچنین اگر پاسخ دارای کسر باشد، پیدا کردن مقدار دقیق کسر بسیار مشکل خواهد بود.
مثال: محل تقاطع خطهای \(3x-y=5\) و \(x+y=-1\) را بیابید.
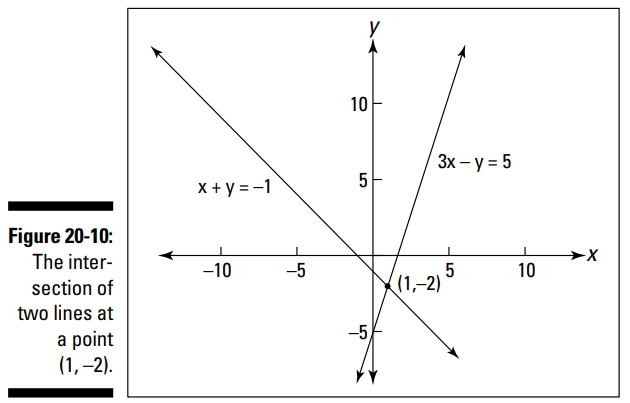
نمودار این دو خط در شکل 10-20 را ببینید. به نظر می رسد خطها در نقطۀ \((1,-2)\) از یکدیگر عبور کرده باشند. این مختصات را در معادلات جایگزین کنید تا پاسخ درست آزمایی گردد:
روش دیگر برای پیدا کردن محل تقاطع دو خط استفاده از تکنیکی می باشد که جایگذاری (substitution) نامیده می شود، شما مقدار \(y\) از یک معادله را در مقدار \(y\) در معادله دیگر جایگزین می کنید و سپس معادله را برای بدست آوردن \(x\) حل می کنید. زیرا شما به دنبال محلی هستید که \(x\) و \(y\) از هر خط یکسان می باشند. سپس می توانید معادله \(y=y\) را بنویسید، این معادله به این معنا می باشد که \(y\) از خط اول برابر با \(y\) در خط دوم می باشد. \(y\) ها را با چیزی که در هر معادله برابر آن می باشند، جایگزین کنید، و سپس معادلات را برای بدست آوردن مقدار \(x\) حل کنید.
مثال: محل تقاطع خطوط \(3x-y=5\) و \(x+y=-1\) را بیابید. (این همان مسأله قبلی می باشد که مرتبه اول با ترسیم نمودار حلش کرده بودیم.)

نقطۀ \((5,1)\) نقطه تقاطع بین دو خط \(x+y=6\) و \(2x-y=9\) می باشد، زیرا این مختصات هر دو معادله را برقرار می سازد:
-
اگر \(x+y=6\) ، سپس با جایگزین کردن \(x=5\) و \(y=1\) خواهیم داشت \(5+1=6\) ، که صحیح می باشد.
-
اگر \(2x-y=9\) سپس با جایگزین کردن \(x=5\) و \(y=1\) به \(2 \times 5 -1=10-1=9\) می رسیم که این هم صحیح می باشد.
این نقطه، تنها مختصاتی می باشد که بر روی هر دو خط قرار دارد.
ترسیم نمودار تقاطع ها
ترسیم با دقت نمودار می تواند محل تقاطع دو خط را به شما بدهد. تنها مشکل اینست که اگر نمودار شما حتی اندکی غیردقیق باشد، ممکن است پاسخ اشتباهی را بدست آورید. همچنین اگر پاسخ دارای کسر باشد، پیدا کردن مقدار دقیق کسر بسیار مشکل خواهد بود.
مثال: محل تقاطع خطهای \(3x-y=5\) و \(x+y=-1\) را بیابید.
نمودار این دو خط در شکل 10-20 را ببینید. به نظر می رسد خطها در نقطۀ \((1,-2)\) از یکدیگر عبور کرده باشند. این مختصات را در معادلات جایگزین کنید تا پاسخ درست آزمایی گردد:
-
اگر \(3x-y=5\) ، سپس با جایگزین کردن مقادیر خواهید داشت \(3 \times 1-(-2)=3+2=5\) ، که صحیح می باشد.
-
اگر \(x+y=-1\) ، سپس با جایگزین کردن مقادیر خواهیم داشت \(1+(-2)=-1\) ، که این هم صحیح می باشد.
یادتان باشد: ترسیم نمودار یک روش غیردقیق برای پیدا کردن محل تقاطع خطوط می باشد. شما باید در هنگام ترسیم نقاط و خطها و رعایت اندازه ها فوق العاده دقیق عمل کنید.
جایگذاری برای پیدا کردن تقاطع ها
روش دیگر برای پیدا کردن محل تقاطع دو خط استفاده از تکنیکی می باشد که جایگذاری (substitution) نامیده می شود، شما مقدار \(y\) از یک معادله را در مقدار \(y\) در معادله دیگر جایگزین می کنید و سپس معادله را برای بدست آوردن \(x\) حل می کنید. زیرا شما به دنبال محلی هستید که \(x\) و \(y\) از هر خط یکسان می باشند. سپس می توانید معادله \(y=y\) را بنویسید، این معادله به این معنا می باشد که \(y\) از خط اول برابر با \(y\) در خط دوم می باشد. \(y\) ها را با چیزی که در هر معادله برابر آن می باشند، جایگزین کنید، و سپس معادلات را برای بدست آوردن مقدار \(x\) حل کنید.
مثال: محل تقاطع خطوط \(3x-y=5\) و \(x+y=-1\) را بیابید. (این همان مسأله قبلی می باشد که مرتبه اول با ترسیم نمودار حلش کرده بودیم.)
-
ابتدا معادلات را در شکل شیب-تقاطع (slope-intercept) بنویسید، که روشی برای حل کردن هر معادله برای \(y\) می باشد.
\(3x-y=5\) به شکل \(y=3x-5\) نوشته می شود و \(x+y=-1\) به شکل \(y=-x-1\) نوشته می شود. این خطها موازی نیستند، و شیب آنها متفاوت می باشد، بنابراین باید دارای یک محل تقاطع باشند.
-
نقاط \(y\) را برابر با یکدیگر قرار داده و معادله را حل کنید.
از \(y=3x-5\) و \(y=-x-1\) ، چیزی را که در معادله اول \(y\) با آن برابر می باشد در \(y\) معادله دوم جایگذاری می کنید، در نتیجه خواهید داشت: \(3x-5=-x-1\)
-
معادله را برای بدست آوردن \(x\) حل کنید.
\(x\) را به هر دو سمت معادله اضافه کنید، و همینطور \(5\) را نیز به هر دو سمت معادله بیفزایید:
$$
3x+x-5+5=-x+x-1+5 \\
4x=4 \\
x=1
$$
این \(1\) را در هر کدام از دو معادله مسأله جایگزین \(x\) کنید تا به \(y=-2\) برسید. محل تقاطع خطوط \((1,-2)\) می باشد.
نکته: این تکنیک چگونگی پیدا کردن پاسخ بدون ترسیم نمودار را به شما نشان داد. اگر خطها موازی باشند، فوراً آشکار می شود، زیرا شیب آنها یکسان می باشد. اگر شیب ها برابر بود، همان اول کار متوقف شوید، زیرا مسأله پاسخی نخواهد داشت. همچنین اگر هر دو معادله صرفاً اشکال مختلفی از یک معادله باشند، این موضوع نیز آشکار خواهد بود: در این حالت وقتی معادله ها را در شکل شیب-تقاطع بازنویسی کنید، دقیقاً یکسان خواهند بود.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: