خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ساده سازی فرآیند ترسیم نمودار با تقاطع ها و تقارن
ترسیم نمودار منحنی ها می تواند به هر میزان که شما بخواهید زمان ببرد، یا به هر سرعتی که بخواهید سریع صورت پذیرد. اگر شما از مزایای ویژگیهای منحنی ها در ترسیم نمودارتان بهره ببرید، می توانید زمان ترسیم نمودار را کاهش بدهید و همینطور دقت خود را بهبود ببخشید. دو ویژگی که شما به سرعت می توانید شناسایی کنید و آنها را بیابید، تقاطع ها (intercepts) و تقارن (symmetry) نمودارها می باشند.

تقاطع های (intercepts) یک نمودار در محل هایی که خطهای نمودار از محورها عبور می کند، ظاهر می شوند. نمودار یک منحنی ممکن است هرگز محوری را قطع نکند، اما وقتیکه چنین باشد (یعنی از محورها عبور کند)، دانستن نقاط تقاطع بسیار سودمند می باشد.
برای مثال، نمودار \(y=-x^2+x+6\) دارای دو طول از مبدأ و یک عرض از مبدأ می باشد:
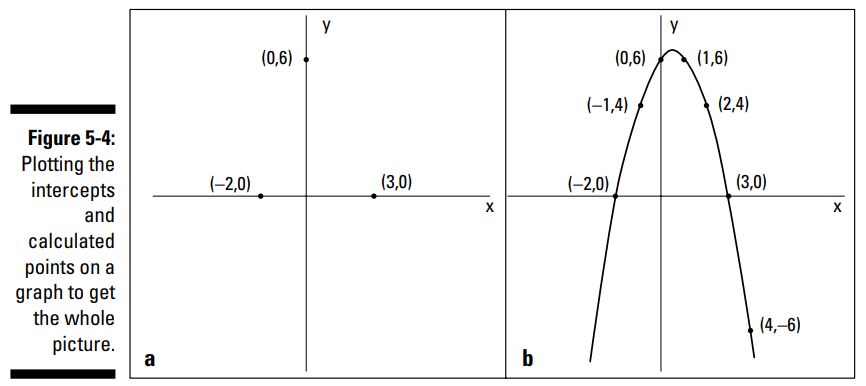
قسمت a از شکل 4-5 تقاطع های مثال قبلی را نشان می دهد که بر روی محورها قرار گرفته اند. نمودار مربوطه اطلاعات زیادی به شما نمی دهد، مگر اینکه آگاه باشید که معادله یک شلجمی (سهمی) می باشد. اگر بدانید که یک سهمی دارید (در فصل 7 در مورد سهمی ها بیشتر توضیح داده ایم)، خواهید دانست که یک منحنی به شکل U از تقاطع ها عبور خواهد کرد. فعلاً، شما می توانید چندین نقطه بیشتر را با روش جایگذاری بیابید و آن نقاط را بر روی صفحه ترسیم کنید تا در ترسیم نمودار نهایی به شما کمک کند. از معادله برای یافتن سایر نقاط که در نمودار به درستی کار می کنند، استفاده کنید، شما می توانید نقاط \( (1, 6), (2, 4), (4, –6), (–1, 4) \) را ترسیم کنید. قسمت b از شکل 4-5 نمودار تکمیل شده را به شما نشان می دهد.
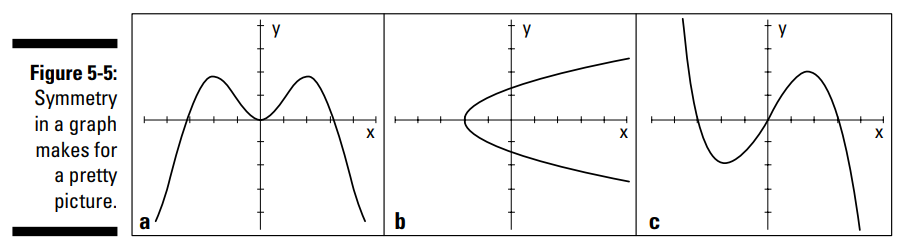
وقتی که یک آیتم از لیست، یا یک چیز جداگانه، متقارن (symmetric) باشد، شما می توانید یک همانی یا الگو را در آن مشاهده کنید. یک نمودار متقارن، نسبت به یکی از محورها، به گونه ای ظاهر می شود که بازتاب وارونه ای از خودش در سمت دیگر محور داشته باشد. یک نمودار متقارن نسبت به مبدأ با یک چرخش \(180\) درجه ای، یکسان به نظر می رسد. شکل 5-5 سه منحنی و سه تقارن را نشان می دهد: تصویر a یک تقارن نسبت به محور \(Y\) را نشان می دهد، تصویر b یک تقارن نسبت به محور \(X\) را نشان می دهد، و تصویر c یک تقارن نسبت به مبدأ نشان می دهد.
تشخیص اینکه نمودار یک منحنی دارای تقارن می باشد به شما کمک می کند نمودار را ترسیم کنید و ویژگیهای آن را تعیین نمایید. بخش های زیر روش های تشخیص وجود تقارن، از روی نمودار یک معادله را به صورت کلی بیان کرده اند.
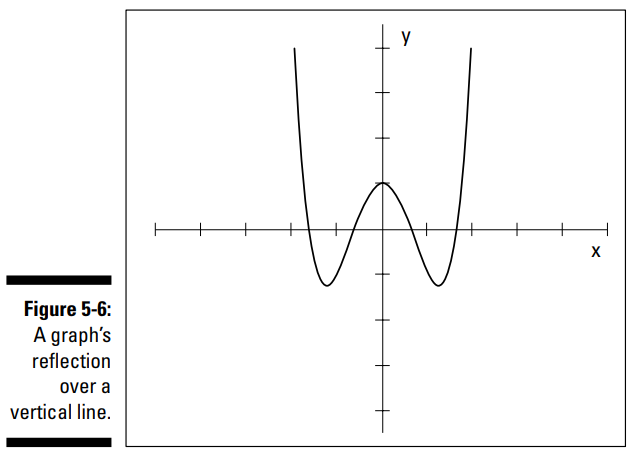
برای مثال، نمودار معادلۀ \(y=x^4-3x^2+1\) نسبت به محور \(Y\) متقارن می باشد. اگر هر \(x\) را با \(-x\) جایگزین کنید، معادله بدون تغییر باقی می ماند. با جایگزین کردن \(-x\) به جای \(x\) ، خواهید داشت: \(y=(-x)^4-3(-x)^2+1=x^4-3x^2+1 \) . عرض از مبدأ برابر با \( (0,1) \) می باشد. برخی از نقاط دیگر عبارت از \( (1,-1) \) ، \( (-1,-1) \) ، و \( (2,5) \) ، \( (-2,5) \) می باشند. توجه داشته باشید که \(y\) برای \(x\) های منفی و مثبت یکسان می باشد. با تقارن نسبت به محور \(Y\) ، برای هر نقطۀ \( (x,y) \) بر روی نمودار، شما همچنین نقطۀ \( (-x,y) \) را نیز می یابید. به دلیل وجود این جفت ها، وقتیکه معادله ای دارای تقارن باشد، پیدا کردن نقاط آسانتر می باشد. شکل 6-5 نمودار معادلۀ \(y=x^4-3x^2+1\) را به شما نشان می دهد.
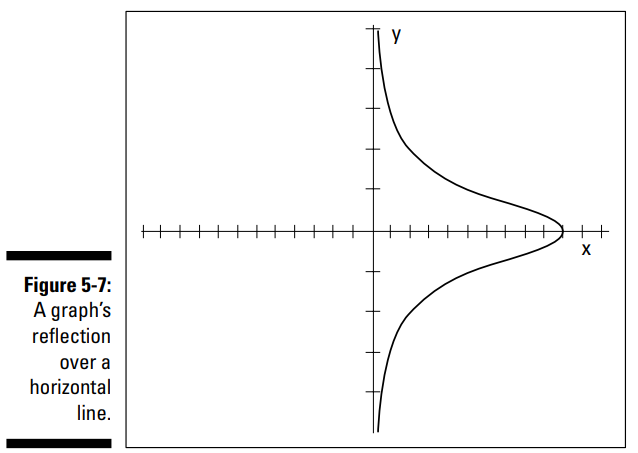
برای مثال، نمودار \(x={10 \over y^2+1}\) نسبت به محور \(X\) متقارن می باشد. هرگاه که مقدار \(y\) را با \(-y\) جایگزین کنید، مقدار\(x\) بدون تغییر خواهد ماند. طول از مبدأ (x-intercept) برابر با \( (10,0) \) می باشد. برخی نقاط دیگر بر روی این نمودار، عبارت از \( (5, 1), (5, –1) \) و \((2, 2), (2, –2)\) و \( (1, 3), (1, –3)\) می باشند. توجه داشته باشید که جفت های نقاط دارای مقادیر مثبت و منفی از \(y\) می باشند اما دارای مقدار یکسانی برای \(x\) می باشند. اینجا جایی است که تقارن وارد می شود: برای هر مختصات \(x\) ، جفت ها هم دارای مقادیر مثبت و هم دارای مقادیر منفی می باشند ـــ در هر دو سمت محور \(X\) . تقارن نسبت به محور \(X\) به این معنا می باشد که به ازاء هر نقطۀ \( (x,y) \) بر روی منحنی، شما همچنین می توانید نقطۀ \( (x,-y) \) را نیز بیابید. این تقارن پیدا کردن نقاط و ترسیم نمودار را ساده تر می کند. نمودار \( x={10 \over y^2+1} \) در تصویر 7-5 نمایش داده شده است.
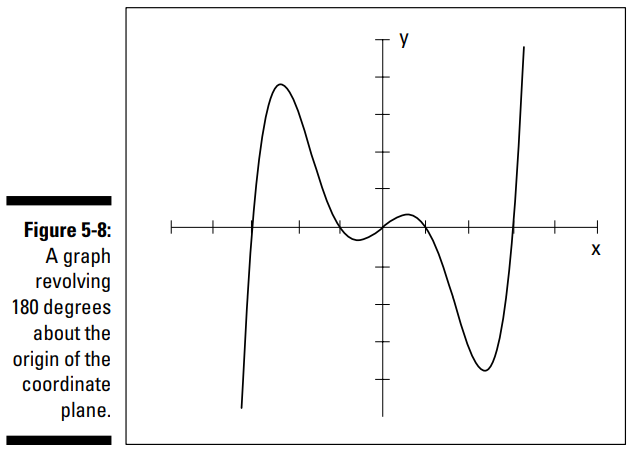
برای مثال، نمودار \( y=x^5-10x^3+9x \) نسبت به مبدأ، متقارن می باشد. وقتیکه هر \(x\) و \(y\) را با \(-x\) و \(-y\) جایگزین کنید، به \( -y=-x^5+10x^3-9x \) می رسید، که برابر با ضرب کردن همۀ جملات در \(-1\) می باشد. در اینجا مبدأ هم طول از مبدأ و هم عرض از مبدأ می باشد. سایر طول از مبدأ ها عبارت از \( (1, 0), (–1, 0) \) و \( (3, 0), (–3, 0) \) می باشند. سایر نقاط بر روی نمودار منحنی شامل \( (2, –30),(–2, 30), (4, 420), (–4, –420)\) می باشند. این نقاط این واقعیت را بیان می کنند که \( (x,y) \) و \( (-x,-y) \) هر دو بر روی نمودار هستند. شکل 8-5 نمودار \( y=x^5-10x^3+9x \) را نشان می دهد (من درجه محور \(Y\) را تغییر داده ام تا هر تیک مارک نشان دهندۀ \(10\) واحد باشد).

پیدا کردن تقاطع های \(x\) و \(y\): (طول از مبدأ و عرض از مبدأ)
تقاطع های (intercepts) یک نمودار در محل هایی که خطهای نمودار از محورها عبور می کند، ظاهر می شوند. نمودار یک منحنی ممکن است هرگز محوری را قطع نکند، اما وقتیکه چنین باشد (یعنی از محورها عبور کند)، دانستن نقاط تقاطع بسیار سودمند می باشد.
یادتان باشد: طول از مبدأ (x-intercepts) همواره در قالب \( (h,0) \) می باشد ـــ مختصات \(y\) برابر با \(0\) می باشد، زیرا نقطه در محور \(X\) قرار دارد. عرض از مبدأ (y-intercepts) دارای قالب \( (0,k) \) می باشد ـــ مختصات \(x\) صفر می باشد، زیرا نقطه در محور \(Y\) قرار دارد. برای پیدا کردن طول از مبدأ و عرض از مبدأ ، به ترتیب اجازه می دهید \(y\) و \(x\) برابر با صفر باشند. برای پیدا کردن طول از مبدأ در یک منحنی، \(y\) را برابر با صفر قرار می دهید و معادله مربوطه را برای یافتن \(x\) حل می کنید. برای پیدا کردن عرض از مبدأ در یک منحنی، \(x\) را برابر با صفر قرار می دهید و معادله را برای یافتن \(y\) حل می کنید.
برای مثال، نمودار \(y=-x^2+x+6\) دارای دو طول از مبدأ و یک عرض از مبدأ می باشد:
-
برای پیدا کردن طول از مبدأ ها، اجازه دهید \(y=0\) باشد. سپس معادله درجه دوم \(0=-x^2+x+6=-(x^2-x-6)\) را خواهید داشت. شما این معادله را با فاکتورگیری آن به \(0=-(x-3)(x+2)\) حل می کنید. دو پاسخ بدست آمده \(x=3\) و \(x=-2\) می باشند، بنابراین دو طول از مبدأ عبارت از \( (3,0) \) و \( (-2,0) \) می باشند.
-
برای پیدا کردن عرض از مبدأ، اجازه دهید \(x=0\) باشد. این به شما معادله \(y=-0+0+6=6\) را می دهد. بنابراین، عرض از مبدأ برابر با \( (0,6) \) می باشد.
قسمت a از شکل 4-5 تقاطع های مثال قبلی را نشان می دهد که بر روی محورها قرار گرفته اند. نمودار مربوطه اطلاعات زیادی به شما نمی دهد، مگر اینکه آگاه باشید که معادله یک شلجمی (سهمی) می باشد. اگر بدانید که یک سهمی دارید (در فصل 7 در مورد سهمی ها بیشتر توضیح داده ایم)، خواهید دانست که یک منحنی به شکل U از تقاطع ها عبور خواهد کرد. فعلاً، شما می توانید چندین نقطه بیشتر را با روش جایگذاری بیابید و آن نقاط را بر روی صفحه ترسیم کنید تا در ترسیم نمودار نهایی به شما کمک کند. از معادله برای یافتن سایر نقاط که در نمودار به درستی کار می کنند، استفاده کنید، شما می توانید نقاط \( (1, 6), (2, 4), (4, –6), (–1, 4) \) را ترسیم کنید. قسمت b از شکل 4-5 نمودار تکمیل شده را به شما نشان می دهد.
تقارن (symmetry) در نمودار
وقتی که یک آیتم از لیست، یا یک چیز جداگانه، متقارن (symmetric) باشد، شما می توانید یک همانی یا الگو را در آن مشاهده کنید. یک نمودار متقارن، نسبت به یکی از محورها، به گونه ای ظاهر می شود که بازتاب وارونه ای از خودش در سمت دیگر محور داشته باشد. یک نمودار متقارن نسبت به مبدأ با یک چرخش \(180\) درجه ای، یکسان به نظر می رسد. شکل 5-5 سه منحنی و سه تقارن را نشان می دهد: تصویر a یک تقارن نسبت به محور \(Y\) را نشان می دهد، تصویر b یک تقارن نسبت به محور \(X\) را نشان می دهد، و تصویر c یک تقارن نسبت به مبدأ نشان می دهد.
تشخیص اینکه نمودار یک منحنی دارای تقارن می باشد به شما کمک می کند نمودار را ترسیم کنید و ویژگیهای آن را تعیین نمایید. بخش های زیر روش های تشخیص وجود تقارن، از روی نمودار یک معادله را به صورت کلی بیان کرده اند.
تقارن نسبت به محور \(Y\)
یادتان باشد: معادله ای در این شکل را در نظر بگیرید: \(y=\) یک عبارت که در آن \(x\) هایی قرار دارند. اگر در این معادله هر \(x\) را با \(-x\) جایگزین کنید، و مقدار \(y\) تغییر نکند، منحنی مربوطه بازتاب وارونه ای از خودش نسبت به محور \(Y\) می باشد. این نمودار شامل نقاط \( (x,y) \) و \( (-x,y) \) می باشد.
برای مثال، نمودار معادلۀ \(y=x^4-3x^2+1\) نسبت به محور \(Y\) متقارن می باشد. اگر هر \(x\) را با \(-x\) جایگزین کنید، معادله بدون تغییر باقی می ماند. با جایگزین کردن \(-x\) به جای \(x\) ، خواهید داشت: \(y=(-x)^4-3(-x)^2+1=x^4-3x^2+1 \) . عرض از مبدأ برابر با \( (0,1) \) می باشد. برخی از نقاط دیگر عبارت از \( (1,-1) \) ، \( (-1,-1) \) ، و \( (2,5) \) ، \( (-2,5) \) می باشند. توجه داشته باشید که \(y\) برای \(x\) های منفی و مثبت یکسان می باشد. با تقارن نسبت به محور \(Y\) ، برای هر نقطۀ \( (x,y) \) بر روی نمودار، شما همچنین نقطۀ \( (-x,y) \) را نیز می یابید. به دلیل وجود این جفت ها، وقتیکه معادله ای دارای تقارن باشد، پیدا کردن نقاط آسانتر می باشد. شکل 6-5 نمودار معادلۀ \(y=x^4-3x^2+1\) را به شما نشان می دهد.
تقارن نسبت به محور \(X\)
یادتان باشد: معادله ای در این شکل را در نظر بگیرید: \(x=\) عبارتی که در آن \(y\) هایی قرار دارند. اگر هر \(y\) را با \(-y\) جایگزین کنید و مقدار \(x\) تغییری نکند، منحنی بازتاب وارونه ای از خودش بر روی محور \(X\) می باشد. این نمودار شامل نقاط \((x,y)\) و \((x,-y)\) می باشد.
برای مثال، نمودار \(x={10 \over y^2+1}\) نسبت به محور \(X\) متقارن می باشد. هرگاه که مقدار \(y\) را با \(-y\) جایگزین کنید، مقدار\(x\) بدون تغییر خواهد ماند. طول از مبدأ (x-intercept) برابر با \( (10,0) \) می باشد. برخی نقاط دیگر بر روی این نمودار، عبارت از \( (5, 1), (5, –1) \) و \((2, 2), (2, –2)\) و \( (1, 3), (1, –3)\) می باشند. توجه داشته باشید که جفت های نقاط دارای مقادیر مثبت و منفی از \(y\) می باشند اما دارای مقدار یکسانی برای \(x\) می باشند. اینجا جایی است که تقارن وارد می شود: برای هر مختصات \(x\) ، جفت ها هم دارای مقادیر مثبت و هم دارای مقادیر منفی می باشند ـــ در هر دو سمت محور \(X\) . تقارن نسبت به محور \(X\) به این معنا می باشد که به ازاء هر نقطۀ \( (x,y) \) بر روی منحنی، شما همچنین می توانید نقطۀ \( (x,-y) \) را نیز بیابید. این تقارن پیدا کردن نقاط و ترسیم نمودار را ساده تر می کند. نمودار \( x={10 \over y^2+1} \) در تصویر 7-5 نمایش داده شده است.
تقارن نسبت به مبدأ
یادتان باشد: معادله ای در این شکل را در نظر بگیرید: \(y=\) عباراتی از \(x\) ها، یا \(x=\) عباراتی از \(y\) ها. اگر تغییر دادن هر عدد به مقدار مخالفش، برابر با ضرب کردن کل عبارت در \(-1\) باشد، منحنی می تواند \(180\) درجه نسبت به مبدأ بچرخد و تصویر خودش باشد. این نمودار شامل نقاط \( (x,y) \) و \( (-x,-y) \) می باشد.
برای مثال، نمودار \( y=x^5-10x^3+9x \) نسبت به مبدأ، متقارن می باشد. وقتیکه هر \(x\) و \(y\) را با \(-x\) و \(-y\) جایگزین کنید، به \( -y=-x^5+10x^3-9x \) می رسید، که برابر با ضرب کردن همۀ جملات در \(-1\) می باشد. در اینجا مبدأ هم طول از مبدأ و هم عرض از مبدأ می باشد. سایر طول از مبدأ ها عبارت از \( (1, 0), (–1, 0) \) و \( (3, 0), (–3, 0) \) می باشند. سایر نقاط بر روی نمودار منحنی شامل \( (2, –30),(–2, 30), (4, 420), (–4, –420)\) می باشند. این نقاط این واقعیت را بیان می کنند که \( (x,y) \) و \( (-x,-y) \) هر دو بر روی نمودار هستند. شکل 8-5 نمودار \( y=x^5-10x^3+9x \) را نشان می دهد (من درجه محور \(Y\) را تغییر داده ام تا هر تیک مارک نشان دهندۀ \(10\) واحد باشد).
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: