خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
بررسی 10 شکل پایه ای

در جبر 2 انواع مختلفی از معادلات و نمودارها را مطالعه می کنید. شما جزئیات خیلی خاصی را در مورد نمودار درجه دوم ها، چندجمله ایها، رادیکال ها، گویا ها، نمایی ها، و لگاریتمی ها در فصلهای مختلف این کتاب که به انواع مختلف اختصاص داده شده است، می توانید پیدا کنید. آنچه را که در این بخش ارائه می دهم یک مرور کلی از برخی از انواع نمودارها می باشد، این بخش طراحی شده است تا به شما کمک کند یک نوع را از نوع دیگر تشخیص بدهید و برای دانستن جزئیات بیشتر آماده گردید. شناخت نمودارهای پایه، نقطه آغازی برای ترسیم نمودار تغییرات در نمودارهای ساده یا منحنی های خیلی پیچیده تر می باشد.

به نظر می رسد نمودارهای پایه ای بیشتر اوقات در جبر 2 رخ دهند. اولین نوع، یعنی خط (line) را، پیشتر در همین فصل پوشش دادم، اما آن را مجدداً در ادامه با نه شکل پایه ای دیگر، ذکر کرده ام.
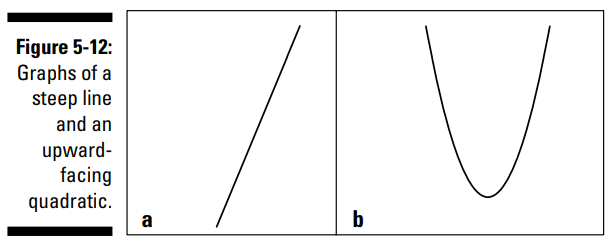
بخش a از شکل 12-5 نمودار یک خط را نشان می دهد. خطها می توانند در حین حرکت از سمت چپ به راست، اوج بگیرند یا اینکه سقوط کنند، یا می توانند افقی یا عمودی باشند. خط نمایش داده شده در بخش a از شکل 12-5 دارای یک شیب مثبت می باشد و نسبتاً تند است. برای جزئیات بیشتر در مورد خطها و سایر شکلها، می توانید بخش ترسیم نمودار خطها را ببینید.
معادله شیب-تقاطع (slope-intercep) یک خط عبارتست از \(y=mx+b\) .
بخش b از شکل 12-5 یک درجه دوم عمومی (چندجمله ای درجه دوم) را نشان می دهد. این منحنی سهمی یا شلجمی نامیده می شود. سهمی ها می توانند مانند این مورد رو به سمت بالا باز شوند، یا رو به سمت پایین، به سمت چپ، و یا به سمت راست باز گردند. شکل ها 3-5 ، 4-5 ، و 5-5 چند نمودار منحنی درجه دوم دیگر را به شما نشان داده اند. (در فصل 3 و همینطور در فصل 7 جزئیات بیشتری در مورد درجه دوم ها مطرح شده است.)
دو معادله عمومی برای درجه دوم ها عبارت از \(y=ax^2+bx+c\) و \(x=ay^2+by+c\) می باشند.
قسمت a از شکل 13-5 نمودار یک درجه سوم (چندجمله ای درجه سوم) را نشان می دهد. یک منحنی مکعبی (یک چندجمله ای با درجه سوم) همانطور که دیده می شود، می تواند یک شکل S مانند داشته باشد، یا در وسط تخت شود و آن چرخشها را نمایان نسازد. یک درجه سوم می تواند به شکلی ظاهر شود که از پایین بیرون بیاید و در سمت راست به بالاترین ارتفاعش برسد، یا می تواند از سمت چپ سقوط کند، چرخشی بکند، و رو به سمت پایین ادامه بدهد (برای اطلاعات بیشتر در مورد چندجمله ایها، فصل 8 را مرور کنید.)
معادله عمومی یک درجه سوم، عبارت از \(y=ax^3+bx^2+cx+d\) می باشد.

قسمت b از شکل 13-5 نمودار یک درجه چهارم (چندجمله ای درجه چهارم) را نشان می دهد. این نمودار یک شکل متمایز شبیه W دارد، اما بسته به تعداد جملاتی که در معادلۀ آن ظاهر می شود، این شکل می تواند مسطح باشد. مشابه درجه دوم (سهمی)، درجه چهارم نیز می تواند رو به سمت پایین باز شود، که در آنصورت به جای W شبیه یک M خواهد بود.
درجه چهارم دارای این معادله عمومی می باشد: \(y=ax^4+bx^3+cx^2+dx+e\)
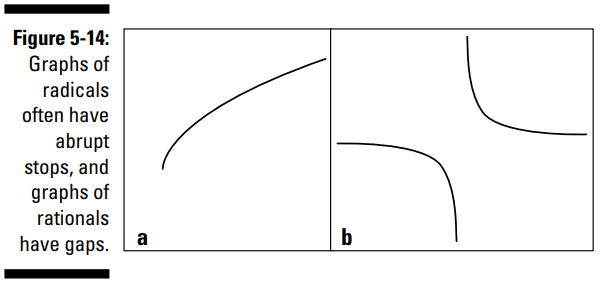
در بخش a از شکل 14-5 ، یک منحنی رادیکال را می بینید، و در بخش b از همین شکل، یک منحنی گویا را می بینید. آنها متضاد یکدیگر به نظر می رسند ، اینطور نیست؟ یک ویژگی عمده در منحنی های رادیکال و گویا که بین آنها مشترک می باشد، اینست که شما نمی توانید آنها را در هر جایی ترسیم کنید. یک منحنی رادیکال دارای معادله ای مانند \(y=\sqrt{x-4}\) می باشد، که ریشه مربع به شما اجازه نمی دهد مقادیری را زیر رادیکال قرار دهید که نتیجه ای منفی را بدهند. در این مورد، شما نمی توانید اعداد کوچکتر از \(4\) را استفاده کنید، بنابراین وفتیکه \(x\) کوچکتر از \(4\) باشد، شما نموداری نخواهید داشت. منحنی رادیکال در بخش a از شکل 14-5 یک توقف ناگهانی را در انتهای سمت چپ نشان می دهد، که در مورد یک منحنی رادیکال عادی می باشد. (در فصل 4 می توانید اطلاعات بیشتری را در مورد رادیکال ها بیابید.)
یک معادله عمومی برای منحنی رادیکال می تواند \(y=\sqrt[n]{x+a}\) باشد، که در آن \(n\) یک عدد زوج می باشد.
معادلات گویا دارای انواع مختلفی از محدودیتها می باشند. وقتیکه معادله یک منحنی شامل یک کسر باشد، آن معادله در معرض این خطا می باشد که صفر در مخرج کسر قرار بگیرد. شما نمی توانید در مخرج کسری صفر داشته باشید، زیرا در ریاضی چنین عددی تعریف نشده است، به همین دلیل هم هست که نمودار منحنی های گویا دارای فضاهای خالی بر رویشان می باشند ___ محل هایی که نمودار با آنها برخوردی ندارد. در بخش b از شکل 14-5 ، شما نمودار معادلۀ \(y={1\over x}\) را می بینید. وقتیکه \(x=0\) باشد، نمودار هیچ مقداری ندارد. (در فصل 9 در مورد توابع گویا، جزئیات بیشتری از این مسأله را خواهید دانست.)
یک معادله عمومی برای منحنی گویا می تواند \(y={a \over x+b}\) باشد.
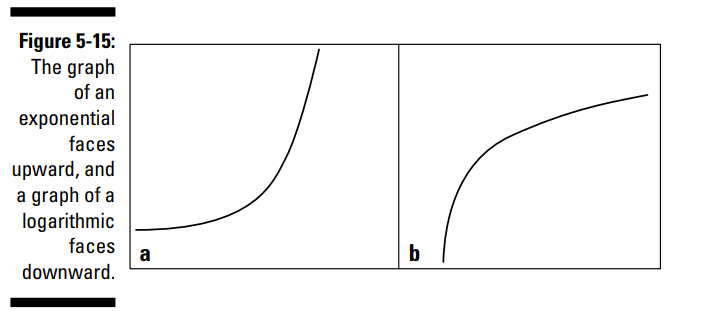
منحنی های نمایی و منحنی های لگاریتمی به نوعی متضاد یکدیگر می باشند، زیرا توابع لگاریتمی و توابع نمایی، معکوس یکدیگر می باشند. بخش a از شکل 15-5 یک منحنی نمایی را به شما نشان می دهد، و بخش b همان تصویر یک منحنی لگاریتمی را به شما نشان می دهد. منحنی های نمایی، دارای یک نقطۀ آغازین یا مقدار اولیه با نام a می باشند، که در حقیقت عرض از مبدأ (y-intercept) است. مقدار b تعیین می کند که آیا منحنی ملایم C شکل، اوج می گیرد یا سقوط می کند. اگر b از یک بزرگتر باشد، منحنی اوج می گیرد. اگر b بین صفر و یک باشد، منحنی سقوط می کند. آنها به طور کلی از سمت چپ به راست اوج می گیرند یا سقوط می کنند، اما آنها رو به سمت بالا هستند و مقعر بطرف بالا (concave up) نامیده می شوند. این کمک می کند تا به آنها به عنوان برف یا شن جمع آوری شده، در منحنی های نرم آنها، فکر کنید. منحنی های لگاریتمی نیز می توانند حین حرکت از سمت چپ به راست، اوج بگیرند یا اینکه سقوط کنند، اما آنها رو به سمت پایین هستند.
شکل عمومی یک منحنی نمایی \(y=ab^x\) می باشد.
شکل عمومی یک منحنی لگاریتمی \(y=log_bx\) می باشد.
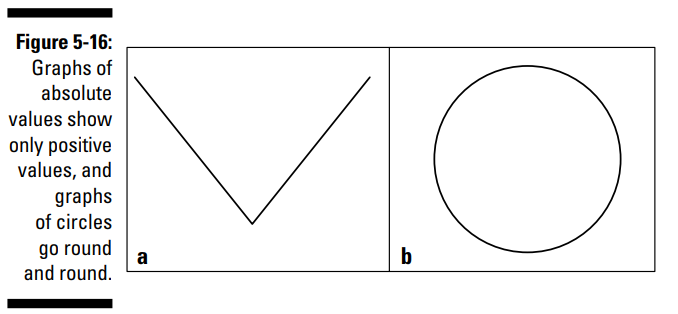
قدرمطلق یک عدد، عددی مثبت می باشد، به همین دلیل هم هست که از ارتباطات قدرمطلق یک منحنی V شکل متمایز به دست می آورید. بخش a از شکل 16-5 یک منحنی معمولی قدرمطلق را نشان می دهد.
معادله عمومی برای قدر مطلق \(y=|ax+b|\) می باشد.
بخش b از شکل 16-5 احتمالاً یکی از شناخته شده ترین اشکال هندسی می باشد. یک دایره با یک فاصله ثابت پیرامون مرکز آن می چرخد. (در فصل 11 در مورد دایره ها و سایر مخروطی ها بحث خواهم کرد.)
دایره ها با مرکزیت مبدأ دارای معادله ای همچون \(x^2+y^2=r^2\) می باشند.

به نظر می رسد نمودارهای پایه ای بیشتر اوقات در جبر 2 رخ دهند. اولین نوع، یعنی خط (line) را، پیشتر در همین فصل پوشش دادم، اما آن را مجدداً در ادامه با نه شکل پایه ای دیگر، ذکر کرده ام.
خطها (Lines) و درجه دوم ها (quadratics)
بخش a از شکل 12-5 نمودار یک خط را نشان می دهد. خطها می توانند در حین حرکت از سمت چپ به راست، اوج بگیرند یا اینکه سقوط کنند، یا می توانند افقی یا عمودی باشند. خط نمایش داده شده در بخش a از شکل 12-5 دارای یک شیب مثبت می باشد و نسبتاً تند است. برای جزئیات بیشتر در مورد خطها و سایر شکلها، می توانید بخش ترسیم نمودار خطها را ببینید.
معادله شیب-تقاطع (slope-intercep) یک خط عبارتست از \(y=mx+b\) .
بخش b از شکل 12-5 یک درجه دوم عمومی (چندجمله ای درجه دوم) را نشان می دهد. این منحنی سهمی یا شلجمی نامیده می شود. سهمی ها می توانند مانند این مورد رو به سمت بالا باز شوند، یا رو به سمت پایین، به سمت چپ، و یا به سمت راست باز گردند. شکل ها 3-5 ، 4-5 ، و 5-5 چند نمودار منحنی درجه دوم دیگر را به شما نشان داده اند. (در فصل 3 و همینطور در فصل 7 جزئیات بیشتری در مورد درجه دوم ها مطرح شده است.)
دو معادله عمومی برای درجه دوم ها عبارت از \(y=ax^2+bx+c\) و \(x=ay^2+by+c\) می باشند.
درجه سوم ها (Cubics) و درجه چهارم ها (quartics)
قسمت a از شکل 13-5 نمودار یک درجه سوم (چندجمله ای درجه سوم) را نشان می دهد. یک منحنی مکعبی (یک چندجمله ای با درجه سوم) همانطور که دیده می شود، می تواند یک شکل S مانند داشته باشد، یا در وسط تخت شود و آن چرخشها را نمایان نسازد. یک درجه سوم می تواند به شکلی ظاهر شود که از پایین بیرون بیاید و در سمت راست به بالاترین ارتفاعش برسد، یا می تواند از سمت چپ سقوط کند، چرخشی بکند، و رو به سمت پایین ادامه بدهد (برای اطلاعات بیشتر در مورد چندجمله ایها، فصل 8 را مرور کنید.)
معادله عمومی یک درجه سوم، عبارت از \(y=ax^3+bx^2+cx+d\) می باشد.
قسمت b از شکل 13-5 نمودار یک درجه چهارم (چندجمله ای درجه چهارم) را نشان می دهد. این نمودار یک شکل متمایز شبیه W دارد، اما بسته به تعداد جملاتی که در معادلۀ آن ظاهر می شود، این شکل می تواند مسطح باشد. مشابه درجه دوم (سهمی)، درجه چهارم نیز می تواند رو به سمت پایین باز شود، که در آنصورت به جای W شبیه یک M خواهد بود.
درجه چهارم دارای این معادله عمومی می باشد: \(y=ax^4+bx^3+cx^2+dx+e\)
رادیکال ها (Radicals) و اعداد گویا (rationals)
در بخش a از شکل 14-5 ، یک منحنی رادیکال را می بینید، و در بخش b از همین شکل، یک منحنی گویا را می بینید. آنها متضاد یکدیگر به نظر می رسند ، اینطور نیست؟ یک ویژگی عمده در منحنی های رادیکال و گویا که بین آنها مشترک می باشد، اینست که شما نمی توانید آنها را در هر جایی ترسیم کنید. یک منحنی رادیکال دارای معادله ای مانند \(y=\sqrt{x-4}\) می باشد، که ریشه مربع به شما اجازه نمی دهد مقادیری را زیر رادیکال قرار دهید که نتیجه ای منفی را بدهند. در این مورد، شما نمی توانید اعداد کوچکتر از \(4\) را استفاده کنید، بنابراین وفتیکه \(x\) کوچکتر از \(4\) باشد، شما نموداری نخواهید داشت. منحنی رادیکال در بخش a از شکل 14-5 یک توقف ناگهانی را در انتهای سمت چپ نشان می دهد، که در مورد یک منحنی رادیکال عادی می باشد. (در فصل 4 می توانید اطلاعات بیشتری را در مورد رادیکال ها بیابید.)
یک معادله عمومی برای منحنی رادیکال می تواند \(y=\sqrt[n]{x+a}\) باشد، که در آن \(n\) یک عدد زوج می باشد.
معادلات گویا دارای انواع مختلفی از محدودیتها می باشند. وقتیکه معادله یک منحنی شامل یک کسر باشد، آن معادله در معرض این خطا می باشد که صفر در مخرج کسر قرار بگیرد. شما نمی توانید در مخرج کسری صفر داشته باشید، زیرا در ریاضی چنین عددی تعریف نشده است، به همین دلیل هم هست که نمودار منحنی های گویا دارای فضاهای خالی بر رویشان می باشند ___ محل هایی که نمودار با آنها برخوردی ندارد. در بخش b از شکل 14-5 ، شما نمودار معادلۀ \(y={1\over x}\) را می بینید. وقتیکه \(x=0\) باشد، نمودار هیچ مقداری ندارد. (در فصل 9 در مورد توابع گویا، جزئیات بیشتری از این مسأله را خواهید دانست.)
یک معادله عمومی برای منحنی گویا می تواند \(y={a \over x+b}\) باشد.
منحنی ها نمایی (Exponential) و لگاریتمی (logarithmic)
منحنی های نمایی و منحنی های لگاریتمی به نوعی متضاد یکدیگر می باشند، زیرا توابع لگاریتمی و توابع نمایی، معکوس یکدیگر می باشند. بخش a از شکل 15-5 یک منحنی نمایی را به شما نشان می دهد، و بخش b همان تصویر یک منحنی لگاریتمی را به شما نشان می دهد. منحنی های نمایی، دارای یک نقطۀ آغازین یا مقدار اولیه با نام a می باشند، که در حقیقت عرض از مبدأ (y-intercept) است. مقدار b تعیین می کند که آیا منحنی ملایم C شکل، اوج می گیرد یا سقوط می کند. اگر b از یک بزرگتر باشد، منحنی اوج می گیرد. اگر b بین صفر و یک باشد، منحنی سقوط می کند. آنها به طور کلی از سمت چپ به راست اوج می گیرند یا سقوط می کنند، اما آنها رو به سمت بالا هستند و مقعر بطرف بالا (concave up) نامیده می شوند. این کمک می کند تا به آنها به عنوان برف یا شن جمع آوری شده، در منحنی های نرم آنها، فکر کنید. منحنی های لگاریتمی نیز می توانند حین حرکت از سمت چپ به راست، اوج بگیرند یا اینکه سقوط کنند، اما آنها رو به سمت پایین هستند.
نکات فنی: هر دوی منحنی های نمایی و لگاریتمی می توانند در جاییکه مقدار قبلی در برخی فاکتورها ضرب گردد، رُشد یا اُفت را مدل سازی کنند. تغییرات با نرخ یکسانی در سراسر منحنی ادامه می یابد، بنابراین شما می توانید منحنی های پایدار رو به سمت بالا یا پایین تولید کنید. (در فصل 10 جزئیات بیشتری در مورد توابع نمایی و لگاریتمی خواهید دانست.)
شکل عمومی یک منحنی نمایی \(y=ab^x\) می باشد.
شکل عمومی یک منحنی لگاریتمی \(y=log_bx\) می باشد.
قدرمطلق ها (Absolute values) و دایره ها (circles)
قدرمطلق یک عدد، عددی مثبت می باشد، به همین دلیل هم هست که از ارتباطات قدرمطلق یک منحنی V شکل متمایز به دست می آورید. بخش a از شکل 16-5 یک منحنی معمولی قدرمطلق را نشان می دهد.
معادله عمومی برای قدر مطلق \(y=|ax+b|\) می باشد.
بخش b از شکل 16-5 احتمالاً یکی از شناخته شده ترین اشکال هندسی می باشد. یک دایره با یک فاصله ثابت پیرامون مرکز آن می چرخد. (در فصل 11 در مورد دایره ها و سایر مخروطی ها بحث خواهم کرد.)
دایره ها با مرکزیت مبدأ دارای معادله ای همچون \(x^2+y^2=r^2\) می باشند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: