خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تقاطع ها و نقاط برگشت در چندجمله ایها

تقاطع های (intercepts) یک چندجمله ای نقاطی هستند که نمودار منحنی چندجمله ای از محور \(X\) و محور \(Y\) عبور می کند. یک تابع چندجمله ای دقیقاً یک عرض از مبدأ (y-intercept) دارد، اما بسته به درجۀ چندجمله ای (توان های متغیرهایش)، می تواند به هر تعداد طول از مبدأ (x-intercepts) داشته باشد. هرچقدر این درجه بیشتر باشد، تعداد طول از مبدأهای احتمالی بیشتر می شود.

طول از مبدأهای یک چندجمله ای را با نامهای ریشه ها (roots)، صفرها (zeros)، یا پاسخها (solutions) می شناسند. ممکن است فکر کنید ریاضیدانان نمی توانند تصمیم بگیرند که این مقادیر را چه بنامند، اما آنها دلایل خودشان را دارند. بسته به کاربردی که مشغول کار بر روی آن هستید، طول از مبدأها نام مناسبی می گیرند. (برای اطلاعات بیشتر و دلایل این نامگذاری ها، قسمت بازی با اسامی را در اینجا بخوانید). نکته زیبا اینست که شما برای بدست آوردن تقاطع ها، روش یکسانی را استفاده می کنید، و مهم نیست که نامش چه باشد. مبادا فکر کنید عرض از مبدأ (y-intercept) از قلم افتاده است، عرض از مبدأ را غالباً مقدار اولیه (initial value) می نامند.
بیشتر مواقع، طول از مبدأها جایی هستند که نمودار چندجمله ای از مقادیر مثبت (مقادیر بالای محور \(X\)) به مقادیر منفی (مقادیر زیر محور \(X\)) می رود یا از مقادیر منفی به مقادیر مثبت می رود. با این حال، گاهی اوقات، مقادیر نمودار در طول از مبدأ علامتشان تغییر نمی کند: این نمودارها به محور \(X\) نزدیک می شوند، سپس به نظر می رسد نظرشان در مورد عبور کردن از محور \(X\) تغییر کرده باشد، آن را در تقاطع ها لمس می کنند و سپس دوباره به همان سمت قبلی محور برمیگردند. ظاهراً فقط هدفشان این بوده که به محور \(X\) بوسه ای بزنند و برگردند!
یک نقطۀ برگشت (turning point) در چندجمله ای جایی است که نمودار منحنی، مسیرش را تغییر می دهد. این تغییر می تواند، تغییر جهت از حرکت رو به بالا، به حرکت رو به پایین و یا برعکس باشد. یک نقطۀ برگشت جایی است که شما می توانید یک مقدار ماکزیمم نسبی (relative maximum value)، یک مقدار ماکزیمم مطلق (absolute maximum value)، یک مقدار مینیمم نسبی (relative minimum value)، یا یک مقدار مینیمم مطلق (absolute minimum value)، از چندجمله ای را پیدا کنید.
همانطور که در فصل 5 به شما معرفی کردم، هر تابعی می تواند دارای یک ماکزیمم مطلق (absolute maximum) یا یک مینیمم مطلق (absolute minimum) باشد ـــ نقطه ای که در آن نمودار تابع به ترتیب مقدار بزرگتر یا کوچکتری از آن را ندارد. برای مثال، یک سهمی که رو به سمت پایین باز می شود، دارای یک ماکزیمم مطلق می باشد ـــ شما هیچ نقطه ای را در منحنی پیدا نخواهید کرد که از آن نقطه بالاتر باشد. به عبارت دیگر، هیچ مقداری از تابع از آن عدد بزرگتر نمی باشد. (برای جزئیات بیشتر در مورد توابع درجه دوم و نمودارهای سهمی آنها، فصل 6 را مرور کنید.) با این حال، برخی از توابع، دارای ماکزیمم نسبی (relative maximum) یا مینیمم نسبی (relative minimum) می باشند:
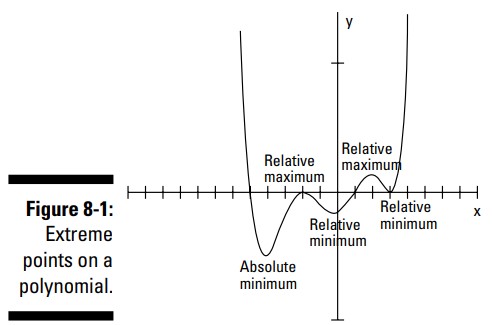
در شکل 1-8، می توانید پنج نقطه برگشت ببینید. دو تا از آنها مقادیر ماکزیمم نسبی هستند، بدین معنا که از تمامی نقاط نزدیک به خودشان بالاترند. سه تا از آنها مقادیر مینیمم هستند، بدین معنا که از تمامی نقاط اطرافشان پایینتر هستند. دو تا از مینیمم ها، مینیمم نسبی هستند، و یکی از آنها مطلقاً پایینترین نقطه در منحنی می باشد. این تابع هیچ مقدار ماکزیمم مطلقی ندارد، زیرا بدون پایان، به بالا رفتن خودش ادامه می دهد.
هنگامی که نمودار یک تابع چندجمله ای را ترسیم می کنید، دانستن تعداد نقاط برگشت و تعداد طول از مبدأهای بالقوه در آن تابع خوب است. اگر نمودار یک چندجمله ای را پیش رویتان داشته باشید، می توانید تعداد طول از مبدأها و نقاط برگشت را شمارش کنید، شما همچنین می توانید در صورت داشتن معادلۀ چندجمله ای این تعداد را تخمین بزنید. تخمین شما در واقع عددی است که بیشترین نقاط ممکن را نشان می دهد. شما می توانید بگویید "در اینجا حداکثر \(m\) تقاطع و حداکثر \(n\) نقطۀ برگشتی می توانند رخ دهند." این تخمین بهترین کاری است که می توانید انجام دهید، و معمولاً می تواند منجر به نتایج خوبی گردد.
برای تعیین قوانینی برای بزرگترین عدد از تقاطع های ممکن و بزرگترین عدد نقاط برگشت ممکن از روی معادلۀ یک چندجمله ای، به شکل کلی یک تابع چندجمله ای می نگرید.
دو معادلۀ تابع زیر را به عنوان مثالی از چندجمله ایها، بررسی کنید. برای تعیین تعداد تقاطع ها و نقاط برگشت ممکن در این تابع، به مقادیر \(n\) نگاه کنید، توانهایی که دارای بالاترین مقدار می باشند:
$$ f(x)=2x^7 + 9x^6 - 75x^5 - 317x^4 + 705x^3 + 2700x^2 $$
این نمودار حداکثر هفت طول از مبدأ دارد (\(7\) بالاترین توان در این تابع می باشد)، و همینطور حداکثر شش نقطه برگشت (\(7-1\)) دارد.
$$ f(x)=6x^6 + 24x^5 - 120x^4 - 480 x^3 + 384 x^2 + 1536x - 2000 $$
این نمودار حداکثر شش طول از مبدأ و پنج نقطه برگشت دارد.
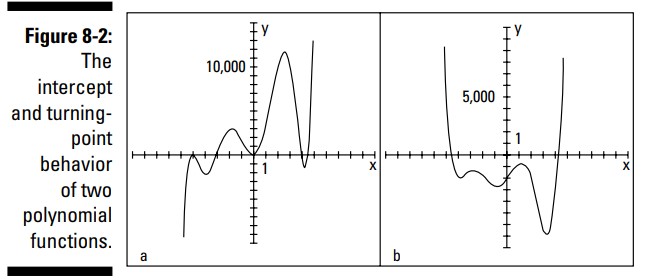
شما می توانید نمودارهای این دو تابع را در شکل 2-8 ببینید. بنابر تابعش، نمودار مثال اول (بخش a از شکل 2-8) حداکثر هفت طول از مبدأ می تواند داشته باشد، اما فقط پنج طول از مبدأ دارد؛ با این حال، تمامی شش نقطه برگشتش را دارد. همچنین می توانید ببینید که دو تا از تقاطع ها از نوع touch-and-go (لمس کن و برو) می باشند، بدین معنا که آنها به محور \(X\) نزدیک می شوند، آن را لمس می کنند و دوباره در مسیر متفاوتی از آن دور می شوند. نمودار مثال دوم (بخش b از شکل 2-8) حداکثر می تواند شش طول از مبدأ داشته باشد، اما فقط دو تا دارد؛ این نمودار تمامی پنج نقطۀ برگشت ممکن را دارا می باشد.
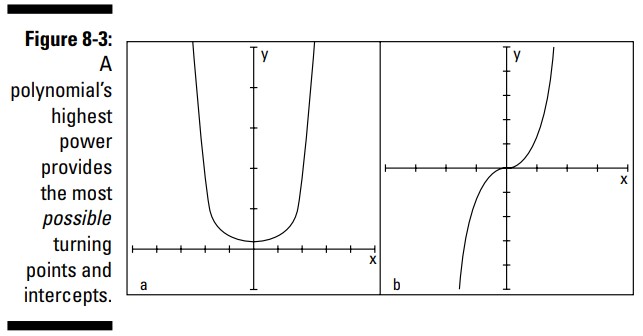
شکل 3-8 برای شما دو مثال چندجمله ای را تدارک دیده است. نمودار \(y=x^8+1\) (بخش a از شکل 3-8) و \(y=x^9\) (بخش b از شکل 3-8) به نظر می رسد احتمالات زیادی داشته باشند ... که به این نتیجه نرسیده اند. نمودار \(y=x^8+1\) ، بنابر قوانین چندجمله ایها، می تواند تا هشت تقاطع و هفت نقطۀ برگشت داشته باشد. اما همانطور که در نمودار می بینید، هیچ تقاطعی ندارد و فقط یک نقطۀ برگشت دارد. نمودار \(y=x^9\) فقط یک تقاطع دارد و هیچ نقطۀ برگشتی ندارد.
شما به سادگی می توانید یک تابع چندجمله ای را برای بدست آوردن عرض از مبدأ آن تابع حل کنید، که در اینصورت فقط یک پاسخ را خواهید یافت. این عرض از مبدأ جایی است که منحنی نمودار از محور \(Y\) عبور می کند، و زمانی این اتفاق می افتد که \(x=0\) باشد. بنابراین، برای تعیین عرض از مبدأ در هر چندجمله ای، به سادگی تمامی \(x\) ها را با صفر جایگزین کنید و آن را برای \(y\) حل کنید (این بخش \(y\) در مختصات آن تقاطع می باشد):
$$
y=3x^4-2x^2+5x-3 \\[2ex]
x=0,y=3(0)^4-2(0)^2+5(0)-3 =-3
$$
عرض از مبدأ برابر با \((0,-3)\) می باشد.
$$
y=8x^5-2x^3+x^2-3x \\[2ex]
x=0, y=8(0)^5-2(0)^3+(0)^2-3(0)=0
$$
عرض از مبدأ برابر با \((0,0)\) می باشد.
بعد از اینکه کار آسانِ حل کردن برای عرض از مبدأ را تکمیل کردید، درخواهید یافت که طول از مبدأها موضوع کاملاً متفاوتی هستند. مقدار \(y\) برای تمامی این طول از مبدأها برابر با صفر می باشد، بنابراین ابتدا \(y=0\)، و سپس حل کنید.
اگرچه، در اینجا، مشابه حل کردن برای عرض از مبدأ، این مزیت که همۀ جملات به جز جملۀ ثابت را با ضرب کردن در صفر ناپدید کنید، را ندارید. هنگام حل کردن برای طول از مبدأها، ممکن است مجبور باشید چندجمله ای را فاکتورگیری کنید یا یک فرآیند پیچیده را انجام بدهید ـــ فرآیند اشاره شده شامل تکنیکهایی می باشد که در ادامۀ همین فصل به آن خواهیم پرداخت. فعلاً، فرآیند فاکتورگیری و قرار دادن فاکتورها برابر با صفر را، برای چند مثال که با دقت و متناسب با دانسته های شما تا اینجا طراحی شده اند، انجام دهید.
برای تعیین طول از مبدأها در سه مثالی که در ادامه آمده است، \(y\) ها را با صفر جایگزین کنید و آنها را برای بدست آوردن \(x\) ها حل کنید:
$$
y=x^2-16 \\[2ex]
y=0,0=x^2-16,x^2=16,x=\pm 4
$$
این مثال را با قانون ریشه مربع (square root rule) که در فصل 3 تشریح شده، حل کردیم.
$$
y=x(x-5)(x-2)(x+1) \\[2ex]
y=0,0=x(x-5)(x-2)(x+1),x=0,5,2,-1
$$
این مثال را با ویژگی ضرب صفر (multiplication property of zero) که در فصل 1 تشریح شده، حل کردیم.
$$
y=x^4(x+3)^8 \\[2ex]
y=0, 0=x^4(x+3)^8, x=0 , -3
$$
این مثال را با ویژگی ضرب صفر حل کردیم. هر دوی این تقاطع ها از ریشه های مکرر (multiple roots) می آیند. (هنگامی که یک پاسخ بیش از یکبار ظاهر شود به آن ریشه های مکرر می گویند، اگر فقط دوبار ظاهر شود به آن ریشۀ مضاعف می گویند). روش دیگر برای نگاه کردن به این مسأله و نگارش شکل فاکتورگیری شدۀ آن این می باشد:
$$
x \cdot x \cdot x \cdot x \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot
(x + 3) = 0
$$
شما می توانید پاسخها را به این شکل لیست کنید:
$$ 0, 0, 0, 0, –3, –3, –3, –3, –3, –3, –3, –3 $$
تعداد دفعاتی که یک ریشه تکرار می شود در هنگام ترسیم نمودار، ارزشمند است. یک ریشه مکرر (multiple root) در محل تقاطع با محور، ظاهر یا انواع نمودار متفاوتی دارد. (در این مورد در ادامۀ همین فصل بیشتر بحث خواهیم داشت.)

طول از مبدأهای یک چندجمله ای را با نامهای ریشه ها (roots)، صفرها (zeros)، یا پاسخها (solutions) می شناسند. ممکن است فکر کنید ریاضیدانان نمی توانند تصمیم بگیرند که این مقادیر را چه بنامند، اما آنها دلایل خودشان را دارند. بسته به کاربردی که مشغول کار بر روی آن هستید، طول از مبدأها نام مناسبی می گیرند. (برای اطلاعات بیشتر و دلایل این نامگذاری ها، قسمت بازی با اسامی را در اینجا بخوانید). نکته زیبا اینست که شما برای بدست آوردن تقاطع ها، روش یکسانی را استفاده می کنید، و مهم نیست که نامش چه باشد. مبادا فکر کنید عرض از مبدأ (y-intercept) از قلم افتاده است، عرض از مبدأ را غالباً مقدار اولیه (initial value) می نامند.
بیشتر مواقع، طول از مبدأها جایی هستند که نمودار چندجمله ای از مقادیر مثبت (مقادیر بالای محور \(X\)) به مقادیر منفی (مقادیر زیر محور \(X\)) می رود یا از مقادیر منفی به مقادیر مثبت می رود. با این حال، گاهی اوقات، مقادیر نمودار در طول از مبدأ علامتشان تغییر نمی کند: این نمودارها به محور \(X\) نزدیک می شوند، سپس به نظر می رسد نظرشان در مورد عبور کردن از محور \(X\) تغییر کرده باشد، آن را در تقاطع ها لمس می کنند و سپس دوباره به همان سمت قبلی محور برمیگردند. ظاهراً فقط هدفشان این بوده که به محور \(X\) بوسه ای بزنند و برگردند!
یک نقطۀ برگشت (turning point) در چندجمله ای جایی است که نمودار منحنی، مسیرش را تغییر می دهد. این تغییر می تواند، تغییر جهت از حرکت رو به بالا، به حرکت رو به پایین و یا برعکس باشد. یک نقطۀ برگشت جایی است که شما می توانید یک مقدار ماکزیمم نسبی (relative maximum value)، یک مقدار ماکزیمم مطلق (absolute maximum value)، یک مقدار مینیمم نسبی (relative minimum value)، یا یک مقدار مینیمم مطلق (absolute minimum value)، از چندجمله ای را پیدا کنید.
تفسیر مقدار نسبی و مقدار مطلق
همانطور که در فصل 5 به شما معرفی کردم، هر تابعی می تواند دارای یک ماکزیمم مطلق (absolute maximum) یا یک مینیمم مطلق (absolute minimum) باشد ـــ نقطه ای که در آن نمودار تابع به ترتیب مقدار بزرگتر یا کوچکتری از آن را ندارد. برای مثال، یک سهمی که رو به سمت پایین باز می شود، دارای یک ماکزیمم مطلق می باشد ـــ شما هیچ نقطه ای را در منحنی پیدا نخواهید کرد که از آن نقطه بالاتر باشد. به عبارت دیگر، هیچ مقداری از تابع از آن عدد بزرگتر نمی باشد. (برای جزئیات بیشتر در مورد توابع درجه دوم و نمودارهای سهمی آنها، فصل 6 را مرور کنید.) با این حال، برخی از توابع، دارای ماکزیمم نسبی (relative maximum) یا مینیمم نسبی (relative minimum) می باشند:
-
ماکزیمم نسبی (Relative maximum): یک نقطه بر روی نمودار ـــ یک مقدار از آن تابع ـــ که نسبتاً بزرگ است؛ آن نقطه نسبت به همۀ چیزهای اطرافش بزرگتر است، اما ممکن است قادر باشید در جای دیگری از نمودار، نقطۀ بزرگتری بیابید.
-
مینیمم نسبی (Relative minimum): یک نقطه بر روی نمودار ـــ یک مقدار از آن تابع ـــ که از تمامی نقاط نزدیک به خودش کوچکتر است؛ آن نقطه نسبت به تمامی نقاط منحنی نزدیکش، کوچکتر یا پایینتر است.
در شکل 1-8، می توانید پنج نقطه برگشت ببینید. دو تا از آنها مقادیر ماکزیمم نسبی هستند، بدین معنا که از تمامی نقاط نزدیک به خودشان بالاترند. سه تا از آنها مقادیر مینیمم هستند، بدین معنا که از تمامی نقاط اطرافشان پایینتر هستند. دو تا از مینیمم ها، مینیمم نسبی هستند، و یکی از آنها مطلقاً پایینترین نقطه در منحنی می باشد. این تابع هیچ مقدار ماکزیمم مطلقی ندارد، زیرا بدون پایان، به بالا رفتن خودش ادامه می دهد.

شمارش تقاطع ها و نقاط برگشت
هنگامی که نمودار یک تابع چندجمله ای را ترسیم می کنید، دانستن تعداد نقاط برگشت و تعداد طول از مبدأهای بالقوه در آن تابع خوب است. اگر نمودار یک چندجمله ای را پیش رویتان داشته باشید، می توانید تعداد طول از مبدأها و نقاط برگشت را شمارش کنید، شما همچنین می توانید در صورت داشتن معادلۀ چندجمله ای این تعداد را تخمین بزنید. تخمین شما در واقع عددی است که بیشترین نقاط ممکن را نشان می دهد. شما می توانید بگویید "در اینجا حداکثر \(m\) تقاطع و حداکثر \(n\) نقطۀ برگشتی می توانند رخ دهند." این تخمین بهترین کاری است که می توانید انجام دهید، و معمولاً می تواند منجر به نتایج خوبی گردد.
برای تعیین قوانینی برای بزرگترین عدد از تقاطع های ممکن و بزرگترین عدد نقاط برگشت ممکن از روی معادلۀ یک چندجمله ای، به شکل کلی یک تابع چندجمله ای می نگرید.
قوانین جبر: در چندجمله ای \(f(x)=a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_1x^1 + a_0 \) ، حداکثر تعداد طول از مبدأها \(n\) می باشد، یعنی همان درجه یا بالاترین توان چند جمله ای. حداکثر تعداد نقاط برگشت برابر با \(n-1\) می باشد، یا یکی کمتر از تعداد تقاطع های ممکن. شما ممکن است تعداد تقاطع کمتری از \(n\) بیابید، یا ممکن هم است دقیقاً همان تعداد تقاطع را بیابید.
نکته: اگر \(n\) عددی فرد باشد، شما فوراً می دانید که حداقل یک طول از مبدأ می توانید بیابید. اگر \(n\) زوج باشد، ممکن است نتوانید هیچ طول از مبدأ ای را بیابید.
دو معادلۀ تابع زیر را به عنوان مثالی از چندجمله ایها، بررسی کنید. برای تعیین تعداد تقاطع ها و نقاط برگشت ممکن در این تابع، به مقادیر \(n\) نگاه کنید، توانهایی که دارای بالاترین مقدار می باشند:
$$ f(x)=2x^7 + 9x^6 - 75x^5 - 317x^4 + 705x^3 + 2700x^2 $$
این نمودار حداکثر هفت طول از مبدأ دارد (\(7\) بالاترین توان در این تابع می باشد)، و همینطور حداکثر شش نقطه برگشت (\(7-1\)) دارد.
$$ f(x)=6x^6 + 24x^5 - 120x^4 - 480 x^3 + 384 x^2 + 1536x - 2000 $$
این نمودار حداکثر شش طول از مبدأ و پنج نقطه برگشت دارد.
شما می توانید نمودارهای این دو تابع را در شکل 2-8 ببینید. بنابر تابعش، نمودار مثال اول (بخش a از شکل 2-8) حداکثر هفت طول از مبدأ می تواند داشته باشد، اما فقط پنج طول از مبدأ دارد؛ با این حال، تمامی شش نقطه برگشتش را دارد. همچنین می توانید ببینید که دو تا از تقاطع ها از نوع touch-and-go (لمس کن و برو) می باشند، بدین معنا که آنها به محور \(X\) نزدیک می شوند، آن را لمس می کنند و دوباره در مسیر متفاوتی از آن دور می شوند. نمودار مثال دوم (بخش b از شکل 2-8) حداکثر می تواند شش طول از مبدأ داشته باشد، اما فقط دو تا دارد؛ این نمودار تمامی پنج نقطۀ برگشت ممکن را دارا می باشد.

شکل 3-8 برای شما دو مثال چندجمله ای را تدارک دیده است. نمودار \(y=x^8+1\) (بخش a از شکل 3-8) و \(y=x^9\) (بخش b از شکل 3-8) به نظر می رسد احتمالات زیادی داشته باشند ... که به این نتیجه نرسیده اند. نمودار \(y=x^8+1\) ، بنابر قوانین چندجمله ایها، می تواند تا هشت تقاطع و هفت نقطۀ برگشت داشته باشد. اما همانطور که در نمودار می بینید، هیچ تقاطعی ندارد و فقط یک نقطۀ برگشت دارد. نمودار \(y=x^9\) فقط یک تقاطع دارد و هیچ نقطۀ برگشتی ندارد.
یادتان باشد: نتیجۀ اخلاقی داستان شکل 3-8 اینست که باید از قوانین چندجمله ایها خردمندانه، بادقت، و شکاکانه استفاده کنید. همچنین، در مورد نمودارهای اصلی چندجمله ایها فکر کنید. این نمودارها منحنی های غلتانی هستند که به آرامی از سمت چپ به راست میروند. آنها از محور \(Y\) دقیقاً یکمرتبه عبور می کنند و ممکن است از محور \(X\) نیز عبور کنند یا از آن عبور نکنند. از شکل استاندارد معادله چندجمله ایها و از شکل فاکتورگیری شدۀ آن اشاراتی را دریافت می کنید. اگر می خواهید این اشارات را مرور کنید به فصل 5 مراجعه دوباره ای داشته باشید.

حل کردن برای تقاطع های چندجمله ای
شما به سادگی می توانید یک تابع چندجمله ای را برای بدست آوردن عرض از مبدأ آن تابع حل کنید، که در اینصورت فقط یک پاسخ را خواهید یافت. این عرض از مبدأ جایی است که منحنی نمودار از محور \(Y\) عبور می کند، و زمانی این اتفاق می افتد که \(x=0\) باشد. بنابراین، برای تعیین عرض از مبدأ در هر چندجمله ای، به سادگی تمامی \(x\) ها را با صفر جایگزین کنید و آن را برای \(y\) حل کنید (این بخش \(y\) در مختصات آن تقاطع می باشد):
$$
y=3x^4-2x^2+5x-3 \\[2ex]
x=0,y=3(0)^4-2(0)^2+5(0)-3 =-3
$$
عرض از مبدأ برابر با \((0,-3)\) می باشد.
$$
y=8x^5-2x^3+x^2-3x \\[2ex]
x=0, y=8(0)^5-2(0)^3+(0)^2-3(0)=0
$$
عرض از مبدأ برابر با \((0,0)\) می باشد.
بعد از اینکه کار آسانِ حل کردن برای عرض از مبدأ را تکمیل کردید، درخواهید یافت که طول از مبدأها موضوع کاملاً متفاوتی هستند. مقدار \(y\) برای تمامی این طول از مبدأها برابر با صفر می باشد، بنابراین ابتدا \(y=0\)، و سپس حل کنید.
اگرچه، در اینجا، مشابه حل کردن برای عرض از مبدأ، این مزیت که همۀ جملات به جز جملۀ ثابت را با ضرب کردن در صفر ناپدید کنید، را ندارید. هنگام حل کردن برای طول از مبدأها، ممکن است مجبور باشید چندجمله ای را فاکتورگیری کنید یا یک فرآیند پیچیده را انجام بدهید ـــ فرآیند اشاره شده شامل تکنیکهایی می باشد که در ادامۀ همین فصل به آن خواهیم پرداخت. فعلاً، فرآیند فاکتورگیری و قرار دادن فاکتورها برابر با صفر را، برای چند مثال که با دقت و متناسب با دانسته های شما تا اینجا طراحی شده اند، انجام دهید.
برای تعیین طول از مبدأها در سه مثالی که در ادامه آمده است، \(y\) ها را با صفر جایگزین کنید و آنها را برای بدست آوردن \(x\) ها حل کنید:
$$
y=x^2-16 \\[2ex]
y=0,0=x^2-16,x^2=16,x=\pm 4
$$
این مثال را با قانون ریشه مربع (square root rule) که در فصل 3 تشریح شده، حل کردیم.
$$
y=x(x-5)(x-2)(x+1) \\[2ex]
y=0,0=x(x-5)(x-2)(x+1),x=0,5,2,-1
$$
این مثال را با ویژگی ضرب صفر (multiplication property of zero) که در فصل 1 تشریح شده، حل کردیم.
$$
y=x^4(x+3)^8 \\[2ex]
y=0, 0=x^4(x+3)^8, x=0 , -3
$$
این مثال را با ویژگی ضرب صفر حل کردیم. هر دوی این تقاطع ها از ریشه های مکرر (multiple roots) می آیند. (هنگامی که یک پاسخ بیش از یکبار ظاهر شود به آن ریشه های مکرر می گویند، اگر فقط دوبار ظاهر شود به آن ریشۀ مضاعف می گویند). روش دیگر برای نگاه کردن به این مسأله و نگارش شکل فاکتورگیری شدۀ آن این می باشد:
$$
x \cdot x \cdot x \cdot x \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot (x + 3) \cdot
(x + 3) = 0
$$
شما می توانید پاسخها را به این شکل لیست کنید:
$$ 0, 0, 0, 0, –3, –3, –3, –3, –3, –3, –3, –3 $$
تعداد دفعاتی که یک ریشه تکرار می شود در هنگام ترسیم نمودار، ارزشمند است. یک ریشه مکرر (multiple root) در محل تقاطع با محور، ظاهر یا انواع نمودار متفاوتی دارد. (در این مورد در ادامۀ همین فصل بیشتر بحث خواهیم داشت.)
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: