خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
حد در توابع گویا

حد (limit) در یک تابع گویا چیزی شبیه محدودیت سرعت در یک جاده می باشد. محدودیت سرعت به شما می گوید (قانوناً) چقدر سریع می توانید بروید. به محض اینکه به محدودیت سرعت نزدیک می شوید، فشاری را که بر روی پدال گاز وارد می کنید بر آن اساس تنظیم می کنید، و سعی می کنید تا به حد مربوطه نزدیک باشید. بیشتر رانندگان تمایل دارند اندکی بیشتر یا اندکی کمتر از حد باشند.

حد در تابع گویا (limit) نیز به همین روش عمل می کند ـــ بر روی یک عدد خاص، یا اندکی بالاتر یا اندکی پایینتر از آن، تمرکز می کند. اگر تابعی دارای حد در عددی خاص باشد، به محض اینکه از سمت چپ یا سمت راست (از سمت پایین یا سمت بالای آن مقدار، به ترتیب) به عدد نامبرده نزدیک شوید، به مکان یکسان یا مقدار تابع یکسانی نزدیک می گردید. آن تابع ضرورتی ندارد که در عددی که به آن نزدیک می شوید تعریف شده باشد (گاهی اوقات در آن عدد تعریف شده است و گاهی هم تعریف نشده است) ـــ می تواند در آن نقطه یک ناپیوستگی وجود داشته باشد. اما، اگر یک حد در آن عدد قرار داشته باشد، مقادیر آن تابع باید واقعاً به یکدیگر نزدیک باشند ـــ اما همدیگر را لمس نکنند.
این نماد را به این شکل می خوانید، "حد تابع \(f(x)\) ، وقتیکه \(x\) به سمت عدد \(a\) میل می کند، برابر با \(L\) می باشد." ضرورتی ندارد عدد \(a\) در دامنۀ این تابع باشد. خواه \(a\) در دامنه باشد، خواه نباشد، شما می توانید در مورد یک حد در یک تابع صحبت کنید. و شما می توانید به \(a\) نزدیک شوید، مادامیکه واقعاً به آن نرسید.
به من اجازه دهید تا این نماد را به محدودیت سرعت که پیشتر مثال زدم، مرتبط کنم. مقدار \(a\) مقدار دقیق فشاری می باشد که شما باید بر روی پدال گاز وارد کنید تا به حد سرعت دقیق برسید ـــ اغلب دستیابی به آن غیرممکن است.
به تابع \(f(x)=x^2+2\) بنگرید. فرض کنید که شما می خواهید بدانید در دو سمت مقدار \(x=1\) چه اتفاقی می افتد. به عبارت دیگر، شما می خواهید بدانید، همچنان که از سمت چپ و سپس از سمت راست به \(1\) نزدیک می شوید، چه اتفاقی برای مقادیر تابع می افتد. جدول 1-9 برخی مقادیر انتخاب شده را به شما نشان می دهد.

همچنان که از سمت چپ یا سمت راست به \(x=1\) نزدیک می شوید، مقدار تابع به عدد \(3\) نزدیک می شود. عدد \(3\) حد این تابع است. ممکن است با خودتان فکر کنید، چرا من صرفاً عدد \(1\) را در تابع جایگذاری نکردم تا به \(f(1)=1^2+2=3\) برسم. پاسخ من اینست که در این مورد شما می توانید این کار را انجام دهید. من از این جدول صرفاً به این منظور استفاده کردم که چگونگی کارکرد مفهوم حد را به شما نشان بدهم.
زیبایی یک حد اینست که می تواند در مواقعی که یک تابع گویا برای عدد خاصی تعریف نشده است نیز بدرستی کار کند. برای مثال، تابع \(y=\frac{x-2}{x^2-2x}\) ، در \(x=0\) و در \(x=2\) ناپیوسته است. شما می توانید این اعداد را با فاکتورگیری مخرج کسر، قرار دادن آن برابر با صفر، و حل کردن آن برای \(x\) پیدا کنید: \(x(x-2)=0\) . این تابع در هنگامی که \(x\) به صفر نزدیک می شود، حدی ندارد، اما وقتیکه \(x\) به دو نزدیک می شود، دارای یک حد می باشد. گاهی اوقات دیدن اعداد به صورت واقعی می تواند سودمند باشد ـــ دیدن اینکه ارزیابی تابع مربوطه با مقادیر مختلف چه نتایجی می دهد ـــ بنابراین من جدول 2-9 را اضافه کرده ام. این جدول نشان می دهد، همینطور که \(x\) از سمت چپ و راست به صفر نزدیک می شود، چه اتفاقی می افتد، و تشریح می کند که این تابع در آن مقدار خاص حدی ندارد.
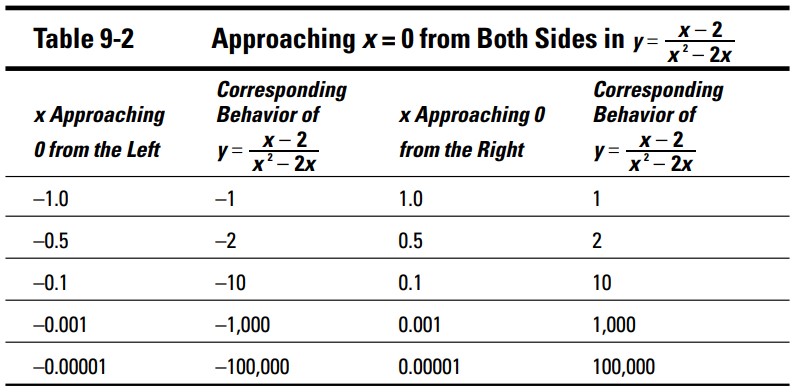
جدول 2-9 به شما نشان می دهد که حد \(\lim \limits_{x \to 0} \frac{x-2}{x^2-2x}\) وجود ندارد. همچنانکه \(x\) از مقادیر زیر صفر نزدیک می شود، مقادیر تابع پایین و پایینتر می آیند و به سمت منفی بی نهایت حرکت می کنند. همینطور که مقادیر بالای صفر می رسند، مقادیر این تابع بالا و بالاتر، رو به سمت مثبت بی نهایت می روند. این دو سمت هرگز با هم به توافقی نمی رسند؛ هیچ حدی وجود ندارد.
جدول 3-9 به شما نشان می دهد، چگونه یک تابع می تواند، حتی در مواقعی که تابع مربوطه در عدد خاصی تعریف نشده باشد، دارای یک حد باشد. با دنبال کردن تابع مثال قبلی، هنگامی که \(x\) به \(2\) نزدیک می شود، شما یک حد را پیدا خواهید کرد.
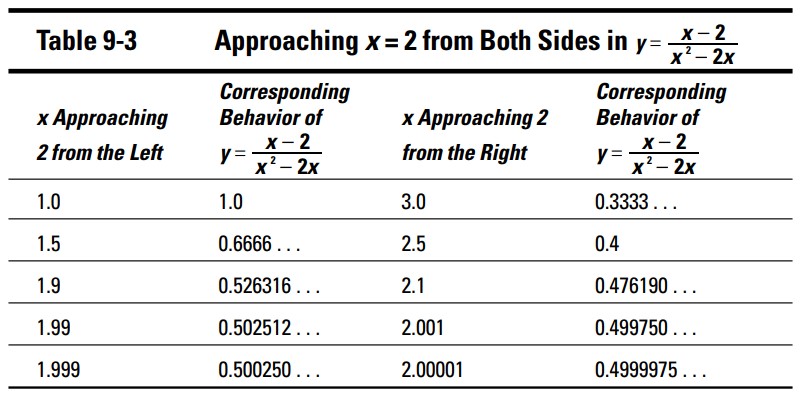
جدول 3-9 نشان می دهد که \(\lim \limits_{x \to 2} \frac{x-2}{x^2-2x}=0.5\) . همینطور که از هر دو سمت \(x\) به \(2\) نزدیکتر و نزدیکتر می شود، اعداد به \(0.5\) نزدیکتر و نزدیکتر می شوند. شما در \(x=2\) یک حد پیدا کردید، حتی با وجود اینکه این تابع در آنجا تعریف نشده است.
اگر دو جدول مثالهای قبلی را بررسی کرده باشید، ممکن است با خودتان فکر کنید که فرآیند یافتن حد کاری طاقت فرسا می باشد. اجازه بدهید تا به شما بگویم که جبر یک روش خیلی آسانتر را به شما پیشنهاد می کند.
جهت حل کردن برای حد وقتیکه \(x=2\) ، در تابع گویایِ \(y=\frac{x-2}{x^2-2x}\) ، ابتدا فاکتورگیری می کنید و سپس کسر را کاهش می دهید:
$$
\require{cancel}
y=\frac{x-2}{x^2-2x}=\frac{\cancel{(x-2)}}{x\cancel{(x-2)}}=\frac{1}{x} $$
اکنون \(x\) را با \(2\) جایگزین می کنید و \(y=0.5\) را بدست می آورید، این می شود حد، وقتیکه \(x=2\). اوه! چقدر ساده! به طور کلی، اگر یک تابع گویا فاکتورگیری شود، سپس شما یک حد را در عددی که از دامنۀ استثناء شده باشد، پیدا خواهید کرد، اگر فاکتورگیری منجر به این شود که این استثناء ناپدید گردد.
اگر در کسری یک صفر در مخرج کسر نشسته باشد، آن کسر دارای مقداری نمی باشد، اما یک صفر تقسیم بر یک صفر دارای یک شکل می باشد ـــ که شکل نامعین (indeterminate form) نامیده می شود. این شکل را به عنوان یک نشانه که شما می توانید بدنبال مقداری برای حد بگردید، در نظر بگیرید.
برای مثال، در اینجا تابعی داریم که در \(x=1\) هیچ حدی ندارد: شما به دنبال چیزی هستید که \(x\) در بیانیۀ حد به آن میل می کند، بنابراین شما تنها در مورد \(1\) نگران هستید.
$$ \lim \limits_{x \to 1} \frac{x^2-4x-5}{x^2-1}=\frac{1-4-5}{1-1}=\frac{-8}{0} $$
این تابع در \(1\) حد ندارد، زیرا عددی بر روی صفر می شود.
اگر این تابع را در \(x=-1\) امتحان کنید، خواهید دید که این تابع دارای یک ناپیوستگی برداشتنی خواهد بود:
$$ \lim \limits_{x \to -1} \frac{x^2-4x-5}{x^2-1}=\frac{1-4(-1)-5}{1-1}=\frac{0}{0} $$
این تابع در \(-1\) دارای یک حد می باشد، زیرا صفر بر روی صفر می شود.
وقتیکه یک تابع گویا در یک مقدار خاص دارای حد نباشد، مقادیر آن تابع و نمودارش باید جایی بروند. یک تابع خاص ممکن است عدد \(3\) را در دامنه اش نداشته باشد، و نمودار آن ممکن است در \(x=3\) دارای یک خط مجانب عمودی باشد. با وجود اینکه این تابع حد ندارد، شما هنوز هم می توانید در مورد اینکه وقتیکه از سمت راست و چپ به \(3\) میل می کند برای تابع چه اتفاقی می افتد، چیزی بگویید. این نمودار هیچ حد عددی در آن نقطه ندارد، اما شما هنوز هم می توانید در مورد رفتار تابع چیزی بگویید. این رفتار به حدهای یکطرفه (one-sided limits) نسبت داده می شود.
علامت تعیین حدهای یکطرفه از سمت چپ یا راست در اینجا نشان داده شده است:
جدول 4-9 مقادیری از تابع \(y=\frac{1}{x-3}\) را نشان می دهد که در \(x=3\) دارای یک خط مجانب افقی می باشند.
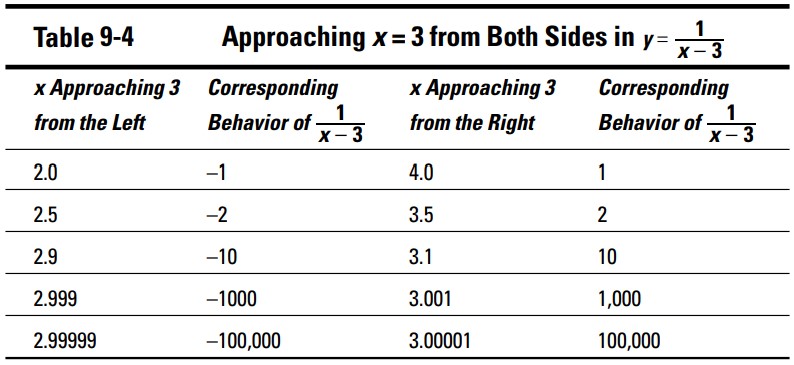
شما حدهای یکطرفه برای این تابع را از روی جدول 4-9 به شرح زیر بیان می کنید:
$$ \lim \limits_{x \to 3^-} \frac{1}{x-3}=-\infty, \lim \limits_{x \to 3^+} \frac{1}{x-3}=+\infty $$
این تابع همچنانکه از مقادیر زیر \(3\) به آن میل می کند، رو به سمت پایین و منفی بی نهایت می رود و همچنانکه از مقادیر بالای \(3\) به آن میل می کند، رو به سمت بالا و مثبت بی نهایت می رود.
بخش قبلی توصیف کرد چگونه مقادیر تابع می توانند همچنانکه \(x\) به اعداد خاصی میل می کند، رو به سمت مثبت بی نهایت یا منفی بی نهایت بروند. در این بخش نیز در مورد بی نهایت صحبت می شود، اما بر روی این تمرکز می کند که توابع گویا، وقتیکه مقادیر \(x\) شان خیلی بزرگ یا خیلی کوچک می شوند (به بی نهایت خودشان میل می کنند)، چه کار می کنند.
یک تابع همچون سهمیِ \(y=x^2+1\) رو به سمت بالا باز می شود. اگر \(x\) را برابر با مقدار واقعاً بزرگی قرار دهید، \(y\) نیز بسیار بزرگ می شود. همچنین، هنگامیکه \(x\) بسیار کوچک باشد (یک عدد منفی بسیار بزرگ)، شما آن مقدار را مربع می سازید، و تبدیل به مثبت می کنید، بنابراین برای آن مقدار \(x\) خیلی کوچک، \(y\) عددی بسیار بزرگ می شود. در نماد تابع، آن چیزی را که برای این تابع رخ می دهد، همچنانکه مقادیر \(x\) به سمت بی نهایت میل می کنند، اینطور توصیف می کنید: \(\lim \limits_{x \to \infty} (x^2+1)=+\infty \)
برای مثال، تابع \(y=-x^3+6\) همچنانکه \(x\) بسیار بزرگ می شود، به سمت منفی بی نهایت میل می کند ـــ اینطور به این مسأله فکر کنید که اگر \(x=1000\)، مقدار \(y\) چه خواهد شد (شما به \(–1,000,000,000+6\) می رسید). از سوی دیگر، وقتیکه \(x=-2\) ، مقدار \(y\) بسیار بزرگ می شود، زیرا شما خواهید داشت \( y = –(–1,000,000,000) + 6\) ، بنابراین این تابع به مثبت بی نهایت میل می کند.
در مورد توابع گویا، حدها در بی نهایت ـــ همچنانکه \(x\) بسیار بزرگ یا بسیار کوچک می شود ـــ ممکن است خاص، محدود، و اعداد قابل توصیف باشند. در واقع، هنگامیکه یک تابع گویا دارای یک خط مجانب افقی باشد، حد آن در بی نهایت برابر با مقدار آن عدد در معادلۀ آن خط مجانب است.
برای مثال، اگر بدنبال خط مجانب افقی در تابع \(y=\frac{4x^2+3}{2x^2-3x-7}\) هستید، با استفاده از قوانینی که در بخشهای پیشین گفتیم، می توانید تعیین کنید که خط مجانب افقی برای این تابع برابر با \(y=2\) می باشد. با استفاده از نماد حد، می توانید این پاسخ را اینطور بنویسید: \(\lim \limits_{x \to \infty} \frac{4x^2+3}{2x^2-3x-7}=2 \)
در اینجا چگونگی کارکرد این ویژگی در هنگام ارزیابی حد در تابع مثال قبلی یعنی \(\frac{4x^2+3}{2x^2-3x-7}\) را می بینید. بالاترین توان متغیر در این تابع برابر با \(x^2\) می باشد، بنابراین هر جمله بر \(x^2\) تقسیم می شود:
$$
\lim \limits_{x \to \infty} \frac{4x^2+3}{2x^2-3x-7} = \\[3ex]
\lim \limits_{x \to \infty} \frac{{4x^2 \over x^2}+{3 \over x^2}}{{2x^2 \over x^2}-{3x \over x^2}-{7 \over x^2}} = \\[3ex]
\lim \limits_{x \to \infty} \frac{4+{3 \over x^2}}{2-{3 \over x}-{7 \over x^2}} = \frac{4+0}{2-0-0}={4 \over2}= 2
$$
حد همچنانکه \(x\) به بی نهایت میل می کند برابر با \(2\) می باشد. همچنانکه پیش بینی کردیم، عدد \(2\) عدد موجود در معادلۀ خط مجانب افقی می باشد. روش سریع برای تعیین خطهای مجانب افقی یک روش ساده تر برای یافتن حدها در بی نهایت است، و همچنین این رویه روش صحیح ریاضی برای انجام آن کار می باشد ـــ و نشان می دهد که چرا قانون دیگر (روش سریع) جواب می دهد. همچنین از این روش سریع برای مسائل بسیار پیچیده تر که در حسابان و ریاضیات عالی یافت می شوند استفاده خواهید کرد.

حد در تابع گویا (limit) نیز به همین روش عمل می کند ـــ بر روی یک عدد خاص، یا اندکی بالاتر یا اندکی پایینتر از آن، تمرکز می کند. اگر تابعی دارای حد در عددی خاص باشد، به محض اینکه از سمت چپ یا سمت راست (از سمت پایین یا سمت بالای آن مقدار، به ترتیب) به عدد نامبرده نزدیک شوید، به مکان یکسان یا مقدار تابع یکسانی نزدیک می گردید. آن تابع ضرورتی ندارد که در عددی که به آن نزدیک می شوید تعریف شده باشد (گاهی اوقات در آن عدد تعریف شده است و گاهی هم تعریف نشده است) ـــ می تواند در آن نقطه یک ناپیوستگی وجود داشته باشد. اما، اگر یک حد در آن عدد قرار داشته باشد، مقادیر آن تابع باید واقعاً به یکدیگر نزدیک باشند ـــ اما همدیگر را لمس نکنند.
یادتان باشد: نمادهای خاص برای حدها (limits) به شرح زیر می باشد:
$$ \lim \limits_{x \to a} f(x)=L $$
$$ \lim \limits_{x \to a} f(x)=L $$
این نماد را به این شکل می خوانید، "حد تابع \(f(x)\) ، وقتیکه \(x\) به سمت عدد \(a\) میل می کند، برابر با \(L\) می باشد." ضرورتی ندارد عدد \(a\) در دامنۀ این تابع باشد. خواه \(a\) در دامنه باشد، خواه نباشد، شما می توانید در مورد یک حد در یک تابع صحبت کنید. و شما می توانید به \(a\) نزدیک شوید، مادامیکه واقعاً به آن نرسید.
به من اجازه دهید تا این نماد را به محدودیت سرعت که پیشتر مثال زدم، مرتبط کنم. مقدار \(a\) مقدار دقیق فشاری می باشد که شما باید بر روی پدال گاز وارد کنید تا به حد سرعت دقیق برسید ـــ اغلب دستیابی به آن غیرممکن است.
به تابع \(f(x)=x^2+2\) بنگرید. فرض کنید که شما می خواهید بدانید در دو سمت مقدار \(x=1\) چه اتفاقی می افتد. به عبارت دیگر، شما می خواهید بدانید، همچنان که از سمت چپ و سپس از سمت راست به \(1\) نزدیک می شوید، چه اتفاقی برای مقادیر تابع می افتد. جدول 1-9 برخی مقادیر انتخاب شده را به شما نشان می دهد.

ترجمۀ جدول 1-9:
Approaching x = 1 from Both Sides in : نزدیک شدن به \(x=1\) از هر دو سمت تابع \(f(x)=x^2+2\)
x Approaching 1 from the Left : \(x\) از سمت چپ به \(1\) نزدیک می شود
Corresponding Behavior in : رفتار متناظر در تابع \(x^2+2\)
x Approaching 1 from the Right : \(x\) از سمت راست به \(1\) نزدیک می شود
Approaching x = 1 from Both Sides in : نزدیک شدن به \(x=1\) از هر دو سمت تابع \(f(x)=x^2+2\)
x Approaching 1 from the Left : \(x\) از سمت چپ به \(1\) نزدیک می شود
Corresponding Behavior in : رفتار متناظر در تابع \(x^2+2\)
x Approaching 1 from the Right : \(x\) از سمت راست به \(1\) نزدیک می شود
همچنان که از سمت چپ یا سمت راست به \(x=1\) نزدیک می شوید، مقدار تابع به عدد \(3\) نزدیک می شود. عدد \(3\) حد این تابع است. ممکن است با خودتان فکر کنید، چرا من صرفاً عدد \(1\) را در تابع جایگذاری نکردم تا به \(f(1)=1^2+2=3\) برسم. پاسخ من اینست که در این مورد شما می توانید این کار را انجام دهید. من از این جدول صرفاً به این منظور استفاده کردم که چگونگی کارکرد مفهوم حد را به شما نشان بدهم.
ارزیابی حدها در ناپیوستگی ها
زیبایی یک حد اینست که می تواند در مواقعی که یک تابع گویا برای عدد خاصی تعریف نشده است نیز بدرستی کار کند. برای مثال، تابع \(y=\frac{x-2}{x^2-2x}\) ، در \(x=0\) و در \(x=2\) ناپیوسته است. شما می توانید این اعداد را با فاکتورگیری مخرج کسر، قرار دادن آن برابر با صفر، و حل کردن آن برای \(x\) پیدا کنید: \(x(x-2)=0\) . این تابع در هنگامی که \(x\) به صفر نزدیک می شود، حدی ندارد، اما وقتیکه \(x\) به دو نزدیک می شود، دارای یک حد می باشد. گاهی اوقات دیدن اعداد به صورت واقعی می تواند سودمند باشد ـــ دیدن اینکه ارزیابی تابع مربوطه با مقادیر مختلف چه نتایجی می دهد ـــ بنابراین من جدول 2-9 را اضافه کرده ام. این جدول نشان می دهد، همینطور که \(x\) از سمت چپ و راست به صفر نزدیک می شود، چه اتفاقی می افتد، و تشریح می کند که این تابع در آن مقدار خاص حدی ندارد.

جدول 2-9 به شما نشان می دهد که حد \(\lim \limits_{x \to 0} \frac{x-2}{x^2-2x}\) وجود ندارد. همچنانکه \(x\) از مقادیر زیر صفر نزدیک می شود، مقادیر تابع پایین و پایینتر می آیند و به سمت منفی بی نهایت حرکت می کنند. همینطور که مقادیر بالای صفر می رسند، مقادیر این تابع بالا و بالاتر، رو به سمت مثبت بی نهایت می روند. این دو سمت هرگز با هم به توافقی نمی رسند؛ هیچ حدی وجود ندارد.
جدول 3-9 به شما نشان می دهد، چگونه یک تابع می تواند، حتی در مواقعی که تابع مربوطه در عدد خاصی تعریف نشده باشد، دارای یک حد باشد. با دنبال کردن تابع مثال قبلی، هنگامی که \(x\) به \(2\) نزدیک می شود، شما یک حد را پیدا خواهید کرد.

جدول 3-9 نشان می دهد که \(\lim \limits_{x \to 2} \frac{x-2}{x^2-2x}=0.5\) . همینطور که از هر دو سمت \(x\) به \(2\) نزدیکتر و نزدیکتر می شود، اعداد به \(0.5\) نزدیکتر و نزدیکتر می شوند. شما در \(x=2\) یک حد پیدا کردید، حتی با وجود اینکه این تابع در آنجا تعریف نشده است.
تعیین کردن یک حد موجود بدون جدول ها
اگر دو جدول مثالهای قبلی را بررسی کرده باشید، ممکن است با خودتان فکر کنید که فرآیند یافتن حد کاری طاقت فرسا می باشد. اجازه بدهید تا به شما بگویم که جبر یک روش خیلی آسانتر را به شما پیشنهاد می کند.
یادتان باشد: توابع دارای ناپیوستگی های برداشتنی در مقادیری که ناپیوستگی وجود دارد دارای حد می باشند. برای یافتن مقادیر این حدها، این مراحل را دنبال کنید:
-
معادلۀ تابع گویا را فاکتورگیری کنید.
-
معادلۀ تابع را کاهش دهید.
-
معادلۀ تابع تجدیدنظر شدۀ جدید را در مقدار \(x\) در مسأله، ارزیابی کنید.
جهت حل کردن برای حد وقتیکه \(x=2\) ، در تابع گویایِ \(y=\frac{x-2}{x^2-2x}\) ، ابتدا فاکتورگیری می کنید و سپس کسر را کاهش می دهید:
$$
\require{cancel}
y=\frac{x-2}{x^2-2x}=\frac{\cancel{(x-2)}}{x\cancel{(x-2)}}=\frac{1}{x} $$
اکنون \(x\) را با \(2\) جایگزین می کنید و \(y=0.5\) را بدست می آورید، این می شود حد، وقتیکه \(x=2\). اوه! چقدر ساده! به طور کلی، اگر یک تابع گویا فاکتورگیری شود، سپس شما یک حد را در عددی که از دامنۀ استثناء شده باشد، پیدا خواهید کرد، اگر فاکتورگیری منجر به این شود که این استثناء ناپدید گردد.
تعیین اینکه کدام توابع دارای حدهایی می باشند
یادتان باشد: برخی از توابع گویا در ناپیوستگی ها دارای حدهایی می باشند و برخی خیر. شما می توانید تعیین کنید که آیا ابتدا با بررسی کردن مقدار \(x\) در آن تابع، در آن تابع خاص بدنبال یک ناپیوستگی برداشتنی بگردید. تمامی \(x\) ها در آن تابع را با عدد موجود در حد جایگزین کنید (چیزی که \(x\) به آن میل می کند). نتیجۀ این جایگزینی به شما می گوید که آیا شما حد دارید یا خیر. شما می توانید از قوانین کلی زیر استفاده کنید:
-
اگر \(\lim \limits_{x \to a} \frac{f(x)}{g(x)}=\frac{\text{some number}}{0}\) ، تابع مربوطه در \(a\) حدی ندارد.
-
اگر \(\lim \limits_{x \to a} \frac{f(x)}{g(x)}=\frac{0}{0}\) ، تابع مربوطه در \(a\) یک حد دارد. شما کسر را کاهش می دهید و معادلۀ تابع شکل گرفتۀ جدید را در \(a\) ارزیابی می کنید (همانطور که در بخش قبلی چگونگی آن را توضیح دادم).
اگر در کسری یک صفر در مخرج کسر نشسته باشد، آن کسر دارای مقداری نمی باشد، اما یک صفر تقسیم بر یک صفر دارای یک شکل می باشد ـــ که شکل نامعین (indeterminate form) نامیده می شود. این شکل را به عنوان یک نشانه که شما می توانید بدنبال مقداری برای حد بگردید، در نظر بگیرید.
برای مثال، در اینجا تابعی داریم که در \(x=1\) هیچ حدی ندارد: شما به دنبال چیزی هستید که \(x\) در بیانیۀ حد به آن میل می کند، بنابراین شما تنها در مورد \(1\) نگران هستید.
$$ \lim \limits_{x \to 1} \frac{x^2-4x-5}{x^2-1}=\frac{1-4-5}{1-1}=\frac{-8}{0} $$
این تابع در \(1\) حد ندارد، زیرا عددی بر روی صفر می شود.
اگر این تابع را در \(x=-1\) امتحان کنید، خواهید دید که این تابع دارای یک ناپیوستگی برداشتنی خواهد بود:
$$ \lim \limits_{x \to -1} \frac{x^2-4x-5}{x^2-1}=\frac{1-4(-1)-5}{1-1}=\frac{0}{0} $$
این تابع در \(-1\) دارای یک حد می باشد، زیرا صفر بر روی صفر می شود.
رفتن به سمت بی نهایت
وقتیکه یک تابع گویا در یک مقدار خاص دارای حد نباشد، مقادیر آن تابع و نمودارش باید جایی بروند. یک تابع خاص ممکن است عدد \(3\) را در دامنه اش نداشته باشد، و نمودار آن ممکن است در \(x=3\) دارای یک خط مجانب عمودی باشد. با وجود اینکه این تابع حد ندارد، شما هنوز هم می توانید در مورد اینکه وقتیکه از سمت راست و چپ به \(3\) میل می کند برای تابع چه اتفاقی می افتد، چیزی بگویید. این نمودار هیچ حد عددی در آن نقطه ندارد، اما شما هنوز هم می توانید در مورد رفتار تابع چیزی بگویید. این رفتار به حدهای یکطرفه (one-sided limits) نسبت داده می شود.
یادتان باشد: یک حد یکطرفه (one-sided limit) به شما می گوید یک تابع در یک مقدار \(x\) همچنانکه از یک سمت یا سمت دیگری به آن میل می کند، چه کاری می کند. حدهای یکطرفه بیشتر محدود کننده هستند؛ آنها تنها از سمت راست یا از سمت چپ درست کار می کنند.
علامت تعیین حدهای یکطرفه از سمت چپ یا راست در اینجا نشان داده شده است:
-
حد همچنانکه \(x\) از سمت چپ به مقدار \(a\) میل می کند برابر است با: \(\lim \limits_{x \to a^-} f(x)\)
-
حد همچنانکه \(x\) از سمت راست به مقدار \(a\) میل می کند برابر است با: \(\lim \limits_{x \to a^+} f(x)\)
نکته: آیا علامت کوچک مثبت یا منفی بعد از \(a\) را دیدید؟ شما می توانید به "از سمت چپ" اینطور فکر کنید که از همان سمتی می آید که تمامی اعداد منفی در خط اعداد از آن سمت می آیند، و به "از سمت راست" از همان سمتی که تمامی اعداد مثبت می آیند، فکر کنید.
جدول 4-9 مقادیری از تابع \(y=\frac{1}{x-3}\) را نشان می دهد که در \(x=3\) دارای یک خط مجانب افقی می باشند.

شما حدهای یکطرفه برای این تابع را از روی جدول 4-9 به شرح زیر بیان می کنید:
$$ \lim \limits_{x \to 3^-} \frac{1}{x-3}=-\infty, \lim \limits_{x \to 3^+} \frac{1}{x-3}=+\infty $$
این تابع همچنانکه از مقادیر زیر \(3\) به آن میل می کند، رو به سمت پایین و منفی بی نهایت می رود و همچنانکه از مقادیر بالای \(3\) به آن میل می کند، رو به سمت بالا و مثبت بی نهایت می رود.
بدست آوردن حدهای گویا در بی نهایت
بخش قبلی توصیف کرد چگونه مقادیر تابع می توانند همچنانکه \(x\) به اعداد خاصی میل می کند، رو به سمت مثبت بی نهایت یا منفی بی نهایت بروند. در این بخش نیز در مورد بی نهایت صحبت می شود، اما بر روی این تمرکز می کند که توابع گویا، وقتیکه مقادیر \(x\) شان خیلی بزرگ یا خیلی کوچک می شوند (به بی نهایت خودشان میل می کنند)، چه کار می کنند.
یک تابع همچون سهمیِ \(y=x^2+1\) رو به سمت بالا باز می شود. اگر \(x\) را برابر با مقدار واقعاً بزرگی قرار دهید، \(y\) نیز بسیار بزرگ می شود. همچنین، هنگامیکه \(x\) بسیار کوچک باشد (یک عدد منفی بسیار بزرگ)، شما آن مقدار را مربع می سازید، و تبدیل به مثبت می کنید، بنابراین برای آن مقدار \(x\) خیلی کوچک، \(y\) عددی بسیار بزرگ می شود. در نماد تابع، آن چیزی را که برای این تابع رخ می دهد، همچنانکه مقادیر \(x\) به سمت بی نهایت میل می کنند، اینطور توصیف می کنید: \(\lim \limits_{x \to \infty} (x^2+1)=+\infty \)
نکته: شما می توانید اینکه یک تابع وقتیکه در یک جهت پیش می رود، به سمت مثبت بی نهایت میل می کند و در وقتیکه در جهت دیگر پیش می رود، به سمت منفی بی نهایت میل می کند، را با همان نمادهای یکسانی که برای حدهای یکطرفه استفاده می کنید، نشان دهید.
برای مثال، تابع \(y=-x^3+6\) همچنانکه \(x\) بسیار بزرگ می شود، به سمت منفی بی نهایت میل می کند ـــ اینطور به این مسأله فکر کنید که اگر \(x=1000\)، مقدار \(y\) چه خواهد شد (شما به \(–1,000,000,000+6\) می رسید). از سوی دیگر، وقتیکه \(x=-2\) ، مقدار \(y\) بسیار بزرگ می شود، زیرا شما خواهید داشت \( y = –(–1,000,000,000) + 6\) ، بنابراین این تابع به مثبت بی نهایت میل می کند.
در مورد توابع گویا، حدها در بی نهایت ـــ همچنانکه \(x\) بسیار بزرگ یا بسیار کوچک می شود ـــ ممکن است خاص، محدود، و اعداد قابل توصیف باشند. در واقع، هنگامیکه یک تابع گویا دارای یک خط مجانب افقی باشد، حد آن در بی نهایت برابر با مقدار آن عدد در معادلۀ آن خط مجانب است.
برای مثال، اگر بدنبال خط مجانب افقی در تابع \(y=\frac{4x^2+3}{2x^2-3x-7}\) هستید، با استفاده از قوانینی که در بخشهای پیشین گفتیم، می توانید تعیین کنید که خط مجانب افقی برای این تابع برابر با \(y=2\) می باشد. با استفاده از نماد حد، می توانید این پاسخ را اینطور بنویسید: \(\lim \limits_{x \to \infty} \frac{4x^2+3}{2x^2-3x-7}=2 \)
قوانین جبر: روش جبری صحیح برای ارزیابی حدها در بی نهایت اینست که هر جمله در تابع گویا را بر بالاترین توان \(x\) در آن کسر تقسیم کنید و سپس به هر جمله بنگرید. در اینجا یک ویژگی مهم برای استفاده هست: همچنانکه \(x\) به بی نهایت میل می کند، هر جمله دارای \(\frac{1}{x}\) در آن به صفر میل می کند ـــ به عبارت دیگر، بسیار کوچک می شود ـــ بنابراین شما می توانید آن جملات را با صفر جایگزین کنید و ساده سازی نمایید.
در اینجا چگونگی کارکرد این ویژگی در هنگام ارزیابی حد در تابع مثال قبلی یعنی \(\frac{4x^2+3}{2x^2-3x-7}\) را می بینید. بالاترین توان متغیر در این تابع برابر با \(x^2\) می باشد، بنابراین هر جمله بر \(x^2\) تقسیم می شود:
$$
\lim \limits_{x \to \infty} \frac{4x^2+3}{2x^2-3x-7} = \\[3ex]
\lim \limits_{x \to \infty} \frac{{4x^2 \over x^2}+{3 \over x^2}}{{2x^2 \over x^2}-{3x \over x^2}-{7 \over x^2}} = \\[3ex]
\lim \limits_{x \to \infty} \frac{4+{3 \over x^2}}{2-{3 \over x}-{7 \over x^2}} = \frac{4+0}{2-0-0}={4 \over2}= 2
$$
حد همچنانکه \(x\) به بی نهایت میل می کند برابر با \(2\) می باشد. همچنانکه پیش بینی کردیم، عدد \(2\) عدد موجود در معادلۀ خط مجانب افقی می باشد. روش سریع برای تعیین خطهای مجانب افقی یک روش ساده تر برای یافتن حدها در بی نهایت است، و همچنین این رویه روش صحیح ریاضی برای انجام آن کار می باشد ـــ و نشان می دهد که چرا قانون دیگر (روش سریع) جواب می دهد. همچنین از این روش سریع برای مسائل بسیار پیچیده تر که در حسابان و ریاضیات عالی یافت می شوند استفاده خواهید کرد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: