نمودارهای توابع گویا می توانند شامل تقاطع ها، خط های مجانب، و ناپیوستگی های برداشتنی باشند (این موضوعات در طول فصل بررسی شدند). در واقع، برخی از نمودارها شامل هر سه این موارد هستند. ترسیم نمودار توابع گویا، در صورتیکه با دقت مهیا شده باشید، نسبتاً ساده می باشد. از هر اطلاعاتی که می توانید از این سو و آن سوی معادلۀ تابع جمع آوری کنید، استفاده کنید، تقاطع ها و خط های مجانب را ترسیم کنید، و سپس چند نقطه ترسیم کنید تا شکل کلی منحنی مشخص گردد.





به عنوان مثال، برای ترسیم نمودار تابع \(y=\frac{x^2-2x-3}{x^2-x-2}\)، ابتدا باید به توانهای صورت و مخرج کسر بنگرید. درجه یا همان بالاترین توان، یکسان می باشد، بنابراین خط مجانب افقی را با ایجاد یک کسر از ضریبهای آغازین، می یابید. هر دوی ضرایب برابر با یک می باشند، و یک تقسیم بر یک هنوز هم یک می شود، بنابراین معادلۀ خط مجانب افقی برابر با \(y=1\) می باشد.

اگرصورت و مخرج کسر را فاکتورگیری کنید، بقیۀ اطلاعات ضروری برای ترسیم نمودار بیشتر قریب الوقوع هستند:
$$
\require{cancel}
y=\frac{(x-3)(x+1)}{(x-2)(x+1)} = \frac{(x-3)\cancel{(x+1)}}{(x-2)\cancel{(x+1)}} = \frac{x-3}{x-2}
$$
شما عامل مشترک \(x+1\) را از صورت و مخرج کسر فاکتور گرفته و بیرون می کشید. این کار دو چیز به شما می گوید. ابتدا، از آنجا که \(x=-1\) مخرج کسر را برابر با صفر قرار می دهد، شما می دانید که \(-1\) در دامنۀ این تابع نمی باشد. بعلاوه، از روی این حقیقت که \(-1\) با فاکتورگیری حذف شد، سیگنالی دریافت می کنید که در \(x=-1\) یک ناپیوستگی برداشتنی وجود دارد. شما می توانید \(-1\) را در معادلۀ جدید جایگذاری کنید تا محل قرارگیری نمودار حفره یا دایرۀ توخالی را بیابید:
$$ y=\frac{x-3}{x-2}=\frac{-1-3}{-1-2}={-4 \over -3}={4\over3} $$
این حفره در \(\biggl(-1,{4\over3} \biggr) \) می باشد. جملات باقیمانده در مخرج کسر به شما می گویند که این تابع دارای یک خط مجانب عمودی در \(x=2\) می باشد. شما با قرار دادن \(x=0\)، عرض از مبدأ را می یابید: \(\biggl(0,{3\over2} \biggr)\) . با قراردادن صورت جدید کسر برابر با صفر و حل کردن آن برای \(x\)، طول از مبدأها را می یابید. وقتیکه \(x-3=0\) ، سپس \(x=3\)، بنابراین طول از مبدأ برابر با \((3,0)\) است. شما این اطلاعات را در نمودار قرار می دهید، که در تصویر 5-9 می بینید. بخش a از تصویر 5-9 به شما چگونگی ترسیم خط های مجانب، تقاطع ها، و ناپیوستگی های برداشتنی را نشان می دهد.


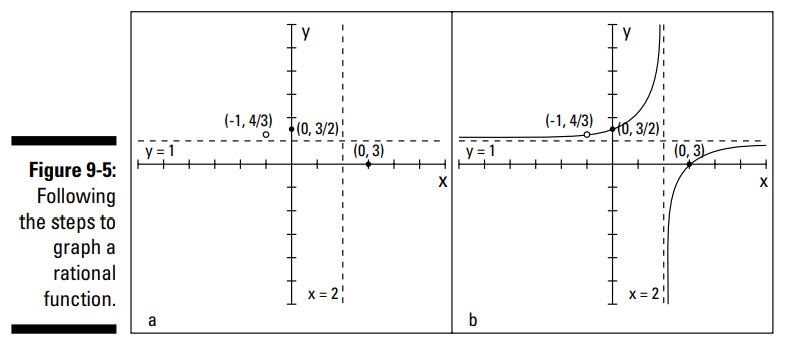
بخش a از شکل 5-9 به نظر می رسد، نشان می دهد که منحنی دارای شکل C نرم در بخشهای بالا و چپ و پایین و راست باشد، که به واسطۀ خطهای مجانب، معکوس یکدیگر می باشند. اگر چند نقطه ترسیم کنید تا این اطلاعات را تایید کنید، خواهید دید که همچنانکه از سمت چپ به \(x=2\) نزدیک می شود، و از سمت راست رو به منفی بی نهایت می رود، نمودار به مثبت بی نهایت میل می کند. شما می توانید در بخش b از شکل 5-9 نمودار کامل شده را ببینید.

نمودارهای سایر توابع گویا، همچون \(y=\frac{x-1}{x^2-5x-6}\) ، قبل از اینکه شما واقعاً نمودار آن را ترسیم نمایید، سرنخ های زیادی به شما نمی دهند. در این مثال، با فاکتورگیری مخرج کسر و قرار دادن آن برابر با صفر، به \((x+1)(x-6)=0\) می رسید؛ خطهای مجانب عمودی در \(x=-1\) و \(x=6\) می باشند. خط مجانب افقی در \(y=0\) می باشد، که محور \(X\) می شود. تنها طول از مبدأ \((1,0)\) می باشد و یک عرض از مبدأ در \(\biggl(0,{1\over6}\biggr)\) قرار گرفته است. بخش a از شکل 6-9 خط های مجانب و تقاطع ها را بر روی نمودار به شما نشان می دهد.


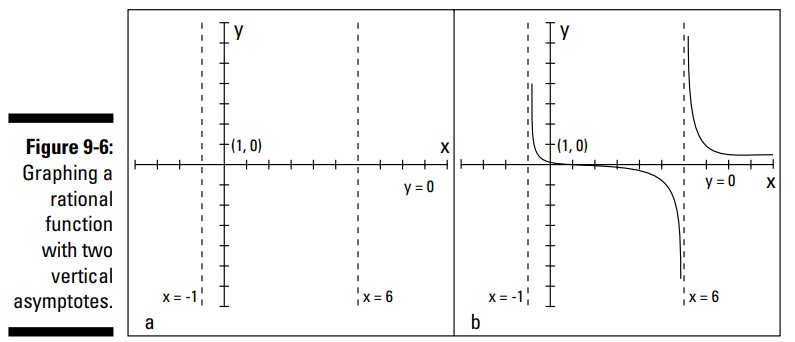
تنها نقطه ای که نمودار این تابع از محور \(X\) عبور می کند در \((1,0)\) می باشد، بنابراین این منحنی باید از سمت چپ بخش میانی که با خطهای مجانب عمودی جدا شده است، بیاید و به سمت راست ادامه پیدا کند. اگر چندین نقطه را امتحان کنید ـــ برای مثال، \(x=0\) و \(x=4\) ـــ به نقاط \(\biggl(0,{1\over6} \biggr)\) و \(\biggl(4,-{3\over10} \biggr)\) می رسید. این نقاط به شما می گویند که این منحنی بالای محور \(X\) و در سمت چپ طول از مبدأ می باشد و همینطور زیر محور \(X\) و در سمت راست این تقاطع می باشد. شما می توانید با استفاده از این اطلاعات یک منحنی ترسیم کنید که از وسط بخش میانی رو به پایین می رود.

سایر نقاط تصادفی که شما ممکن است انتخاب کنید می توانند \(x=-2\) و \(x=7\) باشند. شما نقاطی مشابه این نقاط را انتخاب می کنید تا نقاط نهایی بخشهای سمت راست و چپ نمودار را تست کنید. از روی این مقادیر، به نقاط \(\biggl(-2,-{3\over8} \biggr)\) و \(\biggl(7,{3\over4} \biggr)\) می رسید. این نقاط را روی نمودار قرار دهید و بقیۀ نمودار را که در بخش b از شکل 6-9 نیز نشان داده شده است، ترسیم کنید.