خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
سهمی ها یا شلجمی ها (Parabolas)

سهمی (parabola) یک مخروط U شکل می باشد که در فصل 7 آن را معرفی کردم (سهمی تنها مقطع مخروطی می باشد که در تعریف یک چندجمله ای می گنجد)، تمامی نقاط یک سهمی از یکسری نقطۀ ثابت که کانون (focus) سهمی نامیده می شود، و یک خط ثابت که خط هادی (directrix) سهمی نامیده می شود، فاصلۀ یکسانی دارند. کانون را با حرف \(F\) و خط هادی را با \(y=d\) نشان می دهند. شکل 2-11 برخی از نقاط موجود بر روی یک سهمی و اینکه چگونه هر کدام از آن نقاط با کانون و خط هادی در سهمی فاصله یکسانی دارند را به شما نشان می دهد.


سهمی دارای چندین ویژگی تعریف شدۀ دیگر نیز می باشد. محور تقارن (axis of symmetry) در سهمی، یک خط است که از وسط کانون سهمی عبور می کند و بر خط هادی عمود می باشد (در شکل 2-11 تصور کنید که یک خط از \(F\) عبور کرده باشد). محور تقارن دقیقاً همان کاری را می کند که نامش می گوید: نشان می دهد که یک سهمی چگونه می تواند متقارن باشد. سهمی یک تصویر وارون شده از سمت دیگر محور تقارنش می باشد. ویژگی دیگر رأس (vertex) سهمی می باشد. رأس نقطه ای است که بر منتهی الیه منحنی قرار دارد ـــ پایینترین یا بالاترین نقطه، یا در سمت راست ترین یا در سمت چپ ترین قسمت منحنی. همچنین رأس نقطه ای است که محور تقارن از آن عبور می کند.
سهمی ها می توانند نمودارهایی داشته باشند که به هر سمتی می روند و می توانند رأس هایی در هر نقطه ای از دستگاه مختصات داشته باشند. با این حال، هرگاه که ممکن باشد، شما می خواهید تا با سهمی هایی درگیر شوید که رأس های آنها در مبدأ مختصات می باشد. کنار آمدن با این معادلات ساده تر است و کاربردهایشان ساده تر حل می شوند. بنابراین، در این بخش می خواهم کمی ترتیب آموزش را تغییر بدهم، تا این نوع خاص از سهمی ها را پوشش بدهم.
سهمی هایی که رأس هایشان رو به سمت راست یا چپ باز می شوند دارای معادلۀ استاندارد \(y^2=4ax\) می باشند و به عنوان روابط (relations) شناخته می شوند ـــ شما ارتباطی را بین متغیرها می بینید. این شکل استاندارد اطلاعاتی در مورد کانون، خط هادی، رأس، محور تقارن، و جهت سهمی را در خود بسته بندی کرده است. همچنین این معادله اشاره می کند که آیا سهمی باریک باز شده است یا عریض.
به عنوان مثال، اگر بخواهید اطلاعات مربوط به سهمی \(y^2=8x\) را استخراج کنید، می توانید آن را در شکل \(y^2=4(2)x\) بنویسید. در این مورد، اطلاعات زیر را استخراج می کنید:
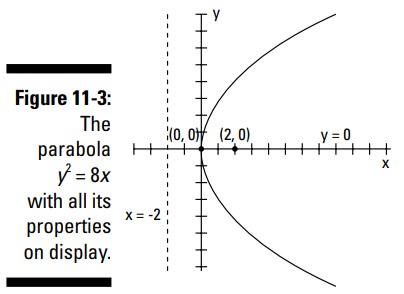
شکل 3-11 نمودار این سهمی، \(y^2=8x\) ، را همراه با تمامی اطلاعات کلیدی آن که بر روی نمودار مشخص شده اند، نشان می دهد.
البته، اگر معادلۀ سهمی دارای یک ضریب زوج، مانند \(y^2=8x\) باشد، استخراج اطلاعات همیشه راحتتر است، اما این فرآیند در مورد اعداد فرد نیز بدرستی کار می کند. فقط تفاوتش در اینست که در صورت فرد بودن ضریب، باید با اعداد کسری سر و کار داشته باشید. به عنوان مثال، شما می توانید سهمیِ \(y^2=7x\) را به شکل \(y^2=4({7\over4})x\) بنویسید، بنابراین مقدار \(a\) برابر با \({7\over4}\) خواهد بود، کانون سهمی برابر با \(({7\over4},0)\) خواهد بود و به همین ترتیب. مقدار \(a\) صرفاً چیزی است که در \(4\) ضرب می شود تا به ضریب اصلی برسد.
سهمی هایی که رو به سمت راست یا چپ باز می شوند، روابط (relations) می باشند، اما سهمی هایی که دارای رأس های باز شده رو به سمت بالا یا پایین می باشند، اندکی خاص ترند. سهمی هایی که رو به سمت بالا یا پایین باز می شوند، توابع می باشند ـــ آنها به ازاء هر مقدار \(x\) فقط یک مقدار \(y\) دارند. (برای کسب اطلاعات بیشتر در مورد توابع، فصل 6 را بازنگری کنید.) سهمی هایی از این نوع دارای معادله استاندارد \(x^2=4ay\) می باشند.
اطلاعاتی که از این سو و آنسوی این معادلۀ استاندارد جمع آوری می کنید، داستانی مشابه آنچیزی که معادلۀ سهمی هایی که رو به سمت راست یا چپ باز می شدند را می گوید؛ اگرچه، بسیاری از قوانین معکوس شده اند.
شما می توانید سهمی \(x^2=-{1\over2}y\) را به شکل \(x^2=4\biggl({-1\over8}\biggr)y\) تبدیل کنید، زیرا شکل کلی به شما اطلاعات سریع، و براحتی در دسترس، می دهد. صرفاً ضریب را بر \(4\) تقسیم کنید، و سپس ضریب را به شکل \(4\) ضربدر نتیجۀ تقسیم بنویسید. شما مقدار ضریب را تغییر نداده اید؛ شما صرفاً ظاهر آن را تغییر داده اید.
در این مورد شما اطلاعات زیر را استخراج می کنید:
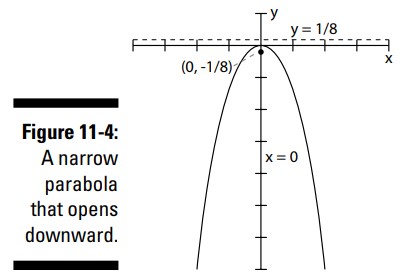
شکل 4-11 نمودار سهمیِ \(x^2=-{1\over2}y\) را همراه با تمامی عناصر آن بر روی شکل، نشان می دهد.
منحنی های سهمی ها می توانند رو به سمت بالا، پایین، به سمت چپ، یا راست باز شوند، اما این منحنی ها همیشه لازم نیست که رأس هایی در مبدأ مختصات داشته باشند. سهمی ها می توانند در هر جایی از نمودار قرار بگیرند. بنابراین، چگونه منحنی ها را مورد جستجو قرار می دهید تا آنها را به نمودار متصل سازید؟ شما به معادلات آنها نگاه می کنید، که تمامی اطلاعات لازم را به شما می دهد تا بدانید آنها در کجای نمودار قرار می گیرند.
شکل استانداری که برای سهمی هایی با رأس هایی در مبدأ مختصات مورد استفاده قرار می گیرد، موارد خاصی از این سهمی های عمومی تر می باشند. اگر مختصات \(h\) و \(k\) را با صفر جایگزین کنید، سهمی های خاصی دارید که در مبدأ لنگر انداخته اند.
یک حرکت در موقعیت رأس (برای مثال، دور از مبدأ) کانون سهمی، خط هادی، و محور تقارن در سهمی را تغییر می دهد. در حالت کلی، حرکت در رأس صرفاً مقداری را به \(h\) یا \(k\) در شکل اصلی، اضافه می کند. به عنوان مثال، وقتیکه رأس در \((h,k)\) باشد، در سهمی هایی که رو به سمت راست باز می شوند، کانون سهمی در \((h+a,k)\) می باشد، و در سهمی هایی که رو به سمت بالا باز می شوند، کانون سهمی در \((h,k+a)\) می باشد. همچنین خط هادی نیز با \(h\) یا \(k\) در معادله اش، تحت تاثیر قرار می گیرد؛ برای سهمی هایی که رو به سمت راست یا چپ باز می شوند، می شود \(x=h-a\) ، و برای سهمی هایی که رو به سمت بالا یا پایین باز می شوند، می شود \(y=k-a\). کل نمودار موقعیتش را تغییر می دهد، اما این تغییر مکان، تاثیری بر روی سمتی که رو به آن باز می شود یا میزان عریض بودن آن ندارد. شکل و جهت یکسان باقی می ماند.
سهمی ها (شلجمی ها) نمودارهای متمایز U شکل دارند، و صرفاً با اندکی اطلاعات، شما می توانید یک نمودار نسبتاً دقیق از یک سهمی خاص را بکشید. اولین مرحله اینست که به تمامی سهمی ها در یکی از شکل های عمومی که پیشتر لیست کردم، فکر کنید.
در اینجا لیست کامل مراحل برای ترسیم نمودار یک سهمی را می بینید ـــ این شکل \((x-h)^2=4a(y-k)\) یا این شکل \((y-k)^2=4a(x-h)\) :
به عنوان مثال، اگر بخواهید نمودار سهمیِ \((y+2)^2=8(x-1)\) را ترسیم کنید، ابتدا توجه داشته باشید که رأس این سهمی در نقطۀ \((1,-2)\) می باشد و رو به سمت راست باز می شود، زیرا \(y\) مربع می باشد و \(4a\) که در اینجا \(4(2)\) است، مثبت می باشد (اگر \(x\) مربع می بود، سهمی رو به سمت بالا یا پایین باز می شد). این نمودار پیرامون محور تقارن، y=-2، نسبتاً عریض می باشد، زیرا \(a=2\) می باشد، که منجر می شود \(|4a|\) بزرگتر از \(1\) گردد. برای یافتن یک نقطۀ تصادفی بر روی نمودار، سعی کنید \(y=6\) باشد و معادله را برای \(x\) حل کنید:
$$
(6+2)^2=8(x-1) \\[2ex]
(8)^2=8(x-1) \\[2ex]
64=8(x-1) \\[2ex]
8=x-1 \\[2ex]
9=x
$$
نقطۀ مثال دیگری که می توانید با فرآیند مشابهی که نقطۀ \((9,6)\) را به شما داد، بیابید، نقطۀ \((5.5,4)\) می باشد. بخش a از شکل 5-11 رأس، محور تقارن، و دو نقطۀ یافت شده را بر روی طرح به شما نشان می دهد.
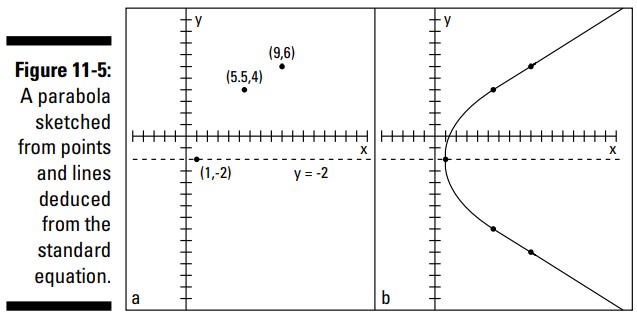
این دو نقطه ای که به صورت تصادفی انتخاب شده اند دارای همتایانی در سمت مقابل محور تقارن می باشند. نقطۀ \((9,6)\) تعداد \(8\) واحد بالای محور تقارن می باشد، بنابراین همتای آن در \(8\) واحد زیر محور تقارن، یعنی در \((9,-10)\) قرار دارد. نقطۀ \((5.5,4)\) تعداد \(6\) واحد بالای محور تقارن می باشد، بنابراین همتای آن در نقطۀ \((5.5,-8)\) می باشد. بخش b از شکل 5-11 این دو نقطۀ جدید و این سهمی را بر روی نمودار به شما نشان می دهد.
ترسیم نمودار سهمی ها به شما کمک می کند تا چگونگی کاربرد آنها را تجسم نمایید، بنابراین شما باید قادر باشید تا در صورت نیاز، سریعاً و با دقت نمودار سهمی ها را ترسیم کنید. یک نمونۀ نسبتاً طبیعی از وقوع سهمی ها، شامل کابل هایی می باشد که بین برج های یک پل معلق قرار دارند. این کابل ها یک منحنی سهمی را شکل می دهند. وضعیت زیر را در نظر بگیرید: یک برقکار می خواهد یک چراغ تزئینی را بر روی کابل یک پل معلق نصب کند، محل نصب این چراغ، به صورت افقی، در فاصلۀ 100 فوتی (feet) از محلی که کابل جاده را در مرکز پل لمس کرده است، می باشد. شما می توانید طرحی را که این برقکار کشیده است در شکل 6-11 ببینید.
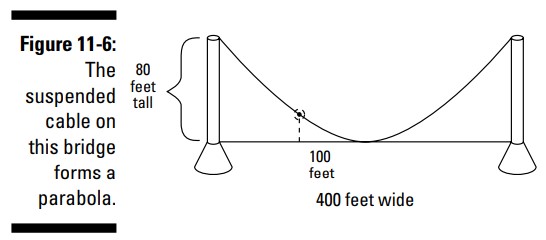
این برقکار نیاز دارد تا بداند ارتفاع کابل در فاصلۀ \(100\) فوتی از مرکز پل چقدر است، تا بتواند چراغ را در آن ارتفاع نصب کند. ارتفاع برجی که کابل را نگهداشته است \(80\) فوت می باشد، و کل عرض پل \(400\) فوت است.
شما می توانید با نوشتن معادلۀ این سهمی که تمامی این پارامترها در آن گنجانده شده اند، به این برقکار کمک کنید تا این مسأله را حل کند. ساده ترین روش برای رسیدگی به این مسأله اینست که اجازه دهید کف جادۀ پل، محور \(X\) و مرکز پل مبدأ مختصات \((0,0)\) باشند. بنابراین، مبدأ، رأس سهمی می باشد. این سهمی رو به سمت بالا باز می شود، بنابراین می توانید از معادلۀ سهمی که رو به بالا باز می شود و رأس آن نیز در مبدأ مختصات قرار دارد، استفاده کنید، این معادله \(x^2=4ay\) می باشد (در همین آموزش به جزئیات مربوط به این نوع سهمی ها پرداخته ایم).
برای اینکه معادله را برای بدست آوردن \(a\) حل کنید، مختصات نقطۀ \((200,80)\) را در معادله قرار دهید. اما بیایید ببینیم، این اعداد به ظاهر تصادفی از کجا بدست آمده اند؟ نصف عرض این پل که کل عرض آن \(400\) فوت است، برابر با \(200\) فوت می باشد. شما از مرکز پل \(200\) فوت به سمت راست مرکز پل می روید و سپس \(80\) فوت رو به سمت بالا می روید، تا به بالاترین نقطه در سمت راستترین قسمت پل برسید. با جایگزین کردن \(x\) در معادله با \(200\) و همچنین جایگزینی \(y\) با \(80\)، به معادلۀ \(40,000=4a(80)\) می رسید. با تقسیم هر سمت از معادله بر \(80\) درخواهید یافت که \(4a\) برابر با \(500\) می باشد، بنابراین معادلۀ این سهمی که نشانگر کابل می باشد، برابر با \(x^2=500y\) می باشد.
خوب، در فاصلۀ \(100\) فوتی از مرکز پل، ارتفاع کابل چقدر می باشد؟ در شکل 6-11 نقطۀ دارای فاصلۀ \(100\) فوت از مرکز پل در سمت چپ مبدأ قرار گرفته است، بنابراین \(-100\) نمایانگر \(x\) می باشد. یک سهمی نسبت به مبدأ آن دارای تقارن می باشد، از این رو مهم نیست که برای حل کردن این مسأله از مثبت یا منفی \(100\) استفاده کنید. اما اگر بخواهیم این تصویر را ملاک قرار دهیم، خواهیم داشت \(x=-100\) ؛ با جایگزین کردن \(x\) در معادله به \((-100)^2=500y\) می رسیم که تبدیل به \(10,000=500y\) می گردد. با تقسیم هر سمت از معادله بر \(500\) به \(y=20\) خواهید رسید. در نقطه ای که برقکار مسألۀ ما می خواهد چراغ را روی کابل نصب کند، ارتفاع کابل \(20\) فوت می باشد. او به یک نردبان نیاز خواهد داشت!
وقتیکه معادلۀ یک سهمی در شکل استاندارد ظاهر شده باشد، شما تمامی اطلاعات مورد نیاز را در اختیار دارید تا نمودار آن را ترسیم کنید یا برخی از ویژگیهای آن مانند جهت و اندازه را تعیین نمایید. با این حال، همۀ معادلات به آن شکل بسته بندی نشده اند. ممکن است ابتدا مجبور شوید قدری کار بر روی آن معادله انجام بدهید تا قادر باشید هر چیزی در مورد آن سهمی را شناسایی کنید.
روشهایی که در اینجا برای بازنویسی معادلۀ یک سهمی به شکل استاندارد آن، مورد استفاده قرار می گیرند، در مورد بازنویسی معادلات دایره ها، بیضی ها، و هذلولی ها نیز کاربرد دارند. شکل استاندارد مقاطع مخروطی یک شکل فاکتورگیری شده می باشد که شما را قادر می سازد تا فوراً اطلاعات مورد نیازتان را شناسایی کنید. موقعیت های مختلف جبری به شکل های استاندارد مختلف نیاز پیدا می کند ـــ شکل صرفاً بستگی به این دارد که به چه چیزی در معادله نیاز دارید.
به عنوان مثال، اگر بخواهید معادلۀ \(x^2+10x-2y+23=0\) را به شکل استاندارد تبدیل کنید، طبق مراحل زیر که شامل روشی با نام کامل کردن مربع (completing the square) می باشد، عمل می کنید (در فصل 3 از روش کامل کردن مربع برای حل کردن معادلات درجه دوم استفاده کردیم):
اکنون این معادله را در شکل استاندارد آن در اختیار دارید. رأس آن در \((-5,-1)\) می باشد؛ رو به سمت بالا باز می شود و نسبتاً عریض می باشد.


سهمی دارای چندین ویژگی تعریف شدۀ دیگر نیز می باشد. محور تقارن (axis of symmetry) در سهمی، یک خط است که از وسط کانون سهمی عبور می کند و بر خط هادی عمود می باشد (در شکل 2-11 تصور کنید که یک خط از \(F\) عبور کرده باشد). محور تقارن دقیقاً همان کاری را می کند که نامش می گوید: نشان می دهد که یک سهمی چگونه می تواند متقارن باشد. سهمی یک تصویر وارون شده از سمت دیگر محور تقارنش می باشد. ویژگی دیگر رأس (vertex) سهمی می باشد. رأس نقطه ای است که بر منتهی الیه منحنی قرار دارد ـــ پایینترین یا بالاترین نقطه، یا در سمت راست ترین یا در سمت چپ ترین قسمت منحنی. همچنین رأس نقطه ای است که محور تقارن از آن عبور می کند.
نگاه کردن به سهمی با رأس هایی در مبدأ
سهمی ها می توانند نمودارهایی داشته باشند که به هر سمتی می روند و می توانند رأس هایی در هر نقطه ای از دستگاه مختصات داشته باشند. با این حال، هرگاه که ممکن باشد، شما می خواهید تا با سهمی هایی درگیر شوید که رأس های آنها در مبدأ مختصات می باشد. کنار آمدن با این معادلات ساده تر است و کاربردهایشان ساده تر حل می شوند. بنابراین، در این بخش می خواهم کمی ترتیب آموزش را تغییر بدهم، تا این نوع خاص از سهمی ها را پوشش بدهم.
باز شدن رو به سمت راست یا چپ
سهمی هایی که رأس هایشان رو به سمت راست یا چپ باز می شوند دارای معادلۀ استاندارد \(y^2=4ax\) می باشند و به عنوان روابط (relations) شناخته می شوند ـــ شما ارتباطی را بین متغیرها می بینید. این شکل استاندارد اطلاعاتی در مورد کانون، خط هادی، رأس، محور تقارن، و جهت سهمی را در خود بسته بندی کرده است. همچنین این معادله اشاره می کند که آیا سهمی باریک باز شده است یا عریض.
قوانین جبر: شکل عمومی یک سهمی با معادلۀ \(y^2=4ax\) اطلاعات زیر را به شما می دهد:
-
کانون (Focus): \((a,0)\)
-
خط هادی (Directrix): \(x=-a\)
-
رأس (Vertex): \((0,0)\)
-
محور تقارن (Axis of symmetry): \(y=0\)
-
باز شدن (Opening): اگر \(a\) مثبت باشد، رو به سمت راست باز می شود؛ اگر \(a\) منفی باشد، رو به سمت چپ باز می شود.
-
شکل (Shape): اگر \(|a|\) کوچکتر از \(1\) باشد، باریک است؛ اگر \(|a|\) بزرگتر از \(1\) باشد، عریض است.
نکات فنی: من از عملیات قدر مطلق | | ، به جای گفتن اینکه \(4a\) بین \(0\) و \(1\) ، یا بین \(-1\) و \(0\) می باشد، استفاده کردم. من فکر می کنم این روش شسته و رفته تری برای برخورد کردن با این قانون می باشد.
به عنوان مثال، اگر بخواهید اطلاعات مربوط به سهمی \(y^2=8x\) را استخراج کنید، می توانید آن را در شکل \(y^2=4(2)x\) بنویسید. در این مورد، اطلاعات زیر را استخراج می کنید:
-
مقدار \(a\) برابر با \(2\) می باشد (از روی \(4 \cdot 2 =8\)).
-
کانون سهمی در \((2,0)\) می باشد.
-
خط هادی سهمی خط \(x=-2\) می باشد.
-
رأس در \((0,0)\) می باشد.
-
محور تقارن برابر با \(y=0\) است.
-
سهمی رو به سمت راست باز می شود.
-
سهمی عریض می باشد، زیرا \(|4(2)|\) بزرگتر از \(1\) می باشد.
شکل 3-11 نمودار این سهمی، \(y^2=8x\) ، را همراه با تمامی اطلاعات کلیدی آن که بر روی نمودار مشخص شده اند، نشان می دهد.

البته، اگر معادلۀ سهمی دارای یک ضریب زوج، مانند \(y^2=8x\) باشد، استخراج اطلاعات همیشه راحتتر است، اما این فرآیند در مورد اعداد فرد نیز بدرستی کار می کند. فقط تفاوتش در اینست که در صورت فرد بودن ضریب، باید با اعداد کسری سر و کار داشته باشید. به عنوان مثال، شما می توانید سهمیِ \(y^2=7x\) را به شکل \(y^2=4({7\over4})x\) بنویسید، بنابراین مقدار \(a\) برابر با \({7\over4}\) خواهد بود، کانون سهمی برابر با \(({7\over4},0)\) خواهد بود و به همین ترتیب. مقدار \(a\) صرفاً چیزی است که در \(4\) ضرب می شود تا به ضریب اصلی برسد.
باز شدن رو به سمت بالا یا پایین
سهمی هایی که رو به سمت راست یا چپ باز می شوند، روابط (relations) می باشند، اما سهمی هایی که دارای رأس های باز شده رو به سمت بالا یا پایین می باشند، اندکی خاص ترند. سهمی هایی که رو به سمت بالا یا پایین باز می شوند، توابع می باشند ـــ آنها به ازاء هر مقدار \(x\) فقط یک مقدار \(y\) دارند. (برای کسب اطلاعات بیشتر در مورد توابع، فصل 6 را بازنگری کنید.) سهمی هایی از این نوع دارای معادله استاندارد \(x^2=4ay\) می باشند.
نکته: اگر متغیر \(y\) مربع باشد، شما می توانید بگویید که یک رابطه دارید (رو به سمت چپ یا راست باز می شود)، به جای اینکه بگویید یک تابع دارید (رو به سمت بالا یا پایین باز می شود). چندجمله ای ها و توابع درجه دوم همگی دارای یک متغیر \(x\) مربع شده می باشند.
اطلاعاتی که از این سو و آنسوی این معادلۀ استاندارد جمع آوری می کنید، داستانی مشابه آنچیزی که معادلۀ سهمی هایی که رو به سمت راست یا چپ باز می شدند را می گوید؛ اگرچه، بسیاری از قوانین معکوس شده اند.
قوانین جبر: از روی شکل کلی سهمیِ \(x^2=4ay\) ، می توانید اطلاعات زیر را بگویید:
-
کانون: \((0,a)\)
-
خط هادی: \(y=-a\)
-
رأس: \((0,0)\)
-
محور تقارن: \(x=0\)
-
جهت باز شدن: اگر \(a\) مثبت باشد، رو به سمت بالا، و اگر \(a\) منفی باشد، رو به سمت پایین باز می شود.
-
شکل: اگر \(|4a|\) کوچکتر از \(1\) باشد، باریک است، و اگر \(|4a|\) بزرگتر از \(1\) باشد، عریض است.
شما می توانید سهمی \(x^2=-{1\over2}y\) را به شکل \(x^2=4\biggl({-1\over8}\biggr)y\) تبدیل کنید، زیرا شکل کلی به شما اطلاعات سریع، و براحتی در دسترس، می دهد. صرفاً ضریب را بر \(4\) تقسیم کنید، و سپس ضریب را به شکل \(4\) ضربدر نتیجۀ تقسیم بنویسید. شما مقدار ضریب را تغییر نداده اید؛ شما صرفاً ظاهر آن را تغییر داده اید.
در این مورد شما اطلاعات زیر را استخراج می کنید:
-
مقدار \(a\) برابر با \(-{1\over8}\) می باشد.
-
کانون سهمی در نقطۀ \(\biggl(0,-{1\over8}\biggr)\) قرار دارد.
-
خط هادی در \(y={1\over8}\) می باشد.
-
رأس در نقطۀ \((0,0)\) می باشد.
-
محور تقارن برابر با \(x=0\) می باشد.
-
نمودار رو به سمت پایین باز می شود.
-
سهمی باریک می باشد، زیرا \(|4(a)|=\biggl|4\biggl(-{1\over8}\biggr)\biggr|=\biggl|-{1\over2}\biggr| \lt 1\) .
شکل 4-11 نمودار سهمیِ \(x^2=-{1\over2}y\) را همراه با تمامی عناصر آن بر روی شکل، نشان می دهد.

مشاهدۀ شکل کلی معادلات سهمی
منحنی های سهمی ها می توانند رو به سمت بالا، پایین، به سمت چپ، یا راست باز شوند، اما این منحنی ها همیشه لازم نیست که رأس هایی در مبدأ مختصات داشته باشند. سهمی ها می توانند در هر جایی از نمودار قرار بگیرند. بنابراین، چگونه منحنی ها را مورد جستجو قرار می دهید تا آنها را به نمودار متصل سازید؟ شما به معادلات آنها نگاه می کنید، که تمامی اطلاعات لازم را به شما می دهد تا بدانید آنها در کجای نمودار قرار می گیرند.
قوانین جبر: هنگامی رأس یک سهمی در نقطۀ \((h,k)\) قرار داشته باشد، شکل کلی معادلۀ آن، یکی از چهار مورد زیر می باشد:
-
باز شدن رو به سمت راست یا چپ: \((y-k)^2=4a(x-h)\) . هنگامی که متغیر \(y\) مربع باشد، سهمی رو به سمت راست یا چپ باز می شود. از روی این معادله، دقیقاً مشابه سهمی هایی که رأس آنها در مبدأ قرار دارد، می توانید اطلاعاتی در مورد عناصر آن را استخراج کنید:
-
اگر \(4a\) مثبت باشد، منحنی رو به سمت راست باز می شود؛ اگر \(4a\) منفی باشد، منحنی رو به سمت چپ باز می شود.
-
اگر \(|4a| \gt 1\) ، سهمی نسبتاً عریض می باشد؛ اگر \(|4a| \lt 1\) ، سهمی نسبتاً باریک می باشد.
-
اگر \(4a\) مثبت باشد، منحنی رو به سمت راست باز می شود؛ اگر \(4a\) منفی باشد، منحنی رو به سمت چپ باز می شود.
-
باز شدن رو به سمت پایین یا بالا: \((x-h)^2=4a(y-k)\) . وقتیکه متغیر \(x\) مربع باشد، سهمی رو به سمت بالا یا پایین باز می شود. اطلاعاتی که می توانید از این معادله استخراج کنید، به شرح زیر می باشد:
-
اگر \(4a\) مثبت باشد، سهمی رو به سمت بالا باز می شود؛ اگر \(4a\) منفی باشد، منحنی رو به سمت پایین باز می شود.
-
اگر \(|4a| \gt 1\)، سهمی عریض می باشد؛ اگر \(|4a| \lt 1\)، سهمی باریک می باشد.
-
اگر \(4a\) مثبت باشد، سهمی رو به سمت بالا باز می شود؛ اگر \(4a\) منفی باشد، منحنی رو به سمت پایین باز می شود.
شکل استانداری که برای سهمی هایی با رأس هایی در مبدأ مختصات مورد استفاده قرار می گیرد، موارد خاصی از این سهمی های عمومی تر می باشند. اگر مختصات \(h\) و \(k\) را با صفر جایگزین کنید، سهمی های خاصی دارید که در مبدأ لنگر انداخته اند.
یک حرکت در موقعیت رأس (برای مثال، دور از مبدأ) کانون سهمی، خط هادی، و محور تقارن در سهمی را تغییر می دهد. در حالت کلی، حرکت در رأس صرفاً مقداری را به \(h\) یا \(k\) در شکل اصلی، اضافه می کند. به عنوان مثال، وقتیکه رأس در \((h,k)\) باشد، در سهمی هایی که رو به سمت راست باز می شوند، کانون سهمی در \((h+a,k)\) می باشد، و در سهمی هایی که رو به سمت بالا باز می شوند، کانون سهمی در \((h,k+a)\) می باشد. همچنین خط هادی نیز با \(h\) یا \(k\) در معادله اش، تحت تاثیر قرار می گیرد؛ برای سهمی هایی که رو به سمت راست یا چپ باز می شوند، می شود \(x=h-a\) ، و برای سهمی هایی که رو به سمت بالا یا پایین باز می شوند، می شود \(y=k-a\). کل نمودار موقعیتش را تغییر می دهد، اما این تغییر مکان، تاثیری بر روی سمتی که رو به آن باز می شود یا میزان عریض بودن آن ندارد. شکل و جهت یکسان باقی می ماند.
ترسیم نمودار سهمی ها
سهمی ها (شلجمی ها) نمودارهای متمایز U شکل دارند، و صرفاً با اندکی اطلاعات، شما می توانید یک نمودار نسبتاً دقیق از یک سهمی خاص را بکشید. اولین مرحله اینست که به تمامی سهمی ها در یکی از شکل های عمومی که پیشتر لیست کردم، فکر کنید.
مراحل ضروری ترسیم نمودار
در اینجا لیست کامل مراحل برای ترسیم نمودار یک سهمی را می بینید ـــ این شکل \((x-h)^2=4a(y-k)\) یا این شکل \((y-k)^2=4a(x-h)\) :
-
تعیین مختصات رأس، \((h,k)\) ، و ترسیم آن.
اگر معادله شامل \((x+h)\) یا \((y+k)\) باشد، شکل آنها را به ترتیب به \((x-[-h])\) یا \((y-[-k])\) تغییر بدهید، تا علامتهای صحیح را تعیین کنید. در واقع، شما صرفاً علامتهای موجود را معکوس می کنید.
-
با نگاه کردن به بخش \(4a\) در معادلۀ عمومی سهمی، تعیین کنید، سهمی رو به کدام سمت باز می شود، و آیا شکل باز شدنِ آن عریض یا باریک می باشد.
-
به نرمی محور تقارن را که از رأس عبور می کند، ترسیم کنید (اگر سهمی رو به سمت بالا یا پایین باز شود، محور تقارن برابر با \(x=h\) می باشد، و اگر سهمی رو به سمت راست یا چپ باز شود، محور تقارن برابر با \(y=k\) می باشد).
-
چندین جفت نقطۀ دیگر نیز بر روی سهمی بیابید و نقاط مرتبط با آنها در سمت دیگر محور تقارن را نیز بیابید تا در ترسیم نمودار به شما کمک کنند.
به عنوان مثال، اگر بخواهید نمودار سهمیِ \((y+2)^2=8(x-1)\) را ترسیم کنید، ابتدا توجه داشته باشید که رأس این سهمی در نقطۀ \((1,-2)\) می باشد و رو به سمت راست باز می شود، زیرا \(y\) مربع می باشد و \(4a\) که در اینجا \(4(2)\) است، مثبت می باشد (اگر \(x\) مربع می بود، سهمی رو به سمت بالا یا پایین باز می شد). این نمودار پیرامون محور تقارن، y=-2، نسبتاً عریض می باشد، زیرا \(a=2\) می باشد، که منجر می شود \(|4a|\) بزرگتر از \(1\) گردد. برای یافتن یک نقطۀ تصادفی بر روی نمودار، سعی کنید \(y=6\) باشد و معادله را برای \(x\) حل کنید:
$$
(6+2)^2=8(x-1) \\[2ex]
(8)^2=8(x-1) \\[2ex]
64=8(x-1) \\[2ex]
8=x-1 \\[2ex]
9=x
$$
نقطۀ مثال دیگری که می توانید با فرآیند مشابهی که نقطۀ \((9,6)\) را به شما داد، بیابید، نقطۀ \((5.5,4)\) می باشد. بخش a از شکل 5-11 رأس، محور تقارن، و دو نقطۀ یافت شده را بر روی طرح به شما نشان می دهد.

این دو نقطه ای که به صورت تصادفی انتخاب شده اند دارای همتایانی در سمت مقابل محور تقارن می باشند. نقطۀ \((9,6)\) تعداد \(8\) واحد بالای محور تقارن می باشد، بنابراین همتای آن در \(8\) واحد زیر محور تقارن، یعنی در \((9,-10)\) قرار دارد. نقطۀ \((5.5,4)\) تعداد \(6\) واحد بالای محور تقارن می باشد، بنابراین همتای آن در نقطۀ \((5.5,-8)\) می باشد. بخش b از شکل 5-11 این دو نقطۀ جدید و این سهمی را بر روی نمودار به شما نشان می دهد.
معمای نصب چراغ تزئینی در پل معلق
ترسیم نمودار سهمی ها به شما کمک می کند تا چگونگی کاربرد آنها را تجسم نمایید، بنابراین شما باید قادر باشید تا در صورت نیاز، سریعاً و با دقت نمودار سهمی ها را ترسیم کنید. یک نمونۀ نسبتاً طبیعی از وقوع سهمی ها، شامل کابل هایی می باشد که بین برج های یک پل معلق قرار دارند. این کابل ها یک منحنی سهمی را شکل می دهند. وضعیت زیر را در نظر بگیرید: یک برقکار می خواهد یک چراغ تزئینی را بر روی کابل یک پل معلق نصب کند، محل نصب این چراغ، به صورت افقی، در فاصلۀ 100 فوتی (feet) از محلی که کابل جاده را در مرکز پل لمس کرده است، می باشد. شما می توانید طرحی را که این برقکار کشیده است در شکل 6-11 ببینید.

این برقکار نیاز دارد تا بداند ارتفاع کابل در فاصلۀ \(100\) فوتی از مرکز پل چقدر است، تا بتواند چراغ را در آن ارتفاع نصب کند. ارتفاع برجی که کابل را نگهداشته است \(80\) فوت می باشد، و کل عرض پل \(400\) فوت است.
شما می توانید با نوشتن معادلۀ این سهمی که تمامی این پارامترها در آن گنجانده شده اند، به این برقکار کمک کنید تا این مسأله را حل کند. ساده ترین روش برای رسیدگی به این مسأله اینست که اجازه دهید کف جادۀ پل، محور \(X\) و مرکز پل مبدأ مختصات \((0,0)\) باشند. بنابراین، مبدأ، رأس سهمی می باشد. این سهمی رو به سمت بالا باز می شود، بنابراین می توانید از معادلۀ سهمی که رو به بالا باز می شود و رأس آن نیز در مبدأ مختصات قرار دارد، استفاده کنید، این معادله \(x^2=4ay\) می باشد (در همین آموزش به جزئیات مربوط به این نوع سهمی ها پرداخته ایم).
برای اینکه معادله را برای بدست آوردن \(a\) حل کنید، مختصات نقطۀ \((200,80)\) را در معادله قرار دهید. اما بیایید ببینیم، این اعداد به ظاهر تصادفی از کجا بدست آمده اند؟ نصف عرض این پل که کل عرض آن \(400\) فوت است، برابر با \(200\) فوت می باشد. شما از مرکز پل \(200\) فوت به سمت راست مرکز پل می روید و سپس \(80\) فوت رو به سمت بالا می روید، تا به بالاترین نقطه در سمت راستترین قسمت پل برسید. با جایگزین کردن \(x\) در معادله با \(200\) و همچنین جایگزینی \(y\) با \(80\)، به معادلۀ \(40,000=4a(80)\) می رسید. با تقسیم هر سمت از معادله بر \(80\) درخواهید یافت که \(4a\) برابر با \(500\) می باشد، بنابراین معادلۀ این سهمی که نشانگر کابل می باشد، برابر با \(x^2=500y\) می باشد.
خوب، در فاصلۀ \(100\) فوتی از مرکز پل، ارتفاع کابل چقدر می باشد؟ در شکل 6-11 نقطۀ دارای فاصلۀ \(100\) فوت از مرکز پل در سمت چپ مبدأ قرار گرفته است، بنابراین \(-100\) نمایانگر \(x\) می باشد. یک سهمی نسبت به مبدأ آن دارای تقارن می باشد، از این رو مهم نیست که برای حل کردن این مسأله از مثبت یا منفی \(100\) استفاده کنید. اما اگر بخواهیم این تصویر را ملاک قرار دهیم، خواهیم داشت \(x=-100\) ؛ با جایگزین کردن \(x\) در معادله به \((-100)^2=500y\) می رسیم که تبدیل به \(10,000=500y\) می گردد. با تقسیم هر سمت از معادله بر \(500\) به \(y=20\) خواهید رسید. در نقطه ای که برقکار مسألۀ ما می خواهد چراغ را روی کابل نصب کند، ارتفاع کابل \(20\) فوت می باشد. او به یک نردبان نیاز خواهد داشت!
تبدیل معادلات سهمی وار به شکل استاندارد
وقتیکه معادلۀ یک سهمی در شکل استاندارد ظاهر شده باشد، شما تمامی اطلاعات مورد نیاز را در اختیار دارید تا نمودار آن را ترسیم کنید یا برخی از ویژگیهای آن مانند جهت و اندازه را تعیین نمایید. با این حال، همۀ معادلات به آن شکل بسته بندی نشده اند. ممکن است ابتدا مجبور شوید قدری کار بر روی آن معادله انجام بدهید تا قادر باشید هر چیزی در مورد آن سهمی را شناسایی کنید.
قوانین جبر: شکل استاندارد یک سهمی برابر با \((x-h)^2=a(y-k)\) یا \((y-k)^2=a(x-h)\) می باشد، که در آن \((h,k)\) رأس سهمی می باشد.
روشهایی که در اینجا برای بازنویسی معادلۀ یک سهمی به شکل استاندارد آن، مورد استفاده قرار می گیرند، در مورد بازنویسی معادلات دایره ها، بیضی ها، و هذلولی ها نیز کاربرد دارند. شکل استاندارد مقاطع مخروطی یک شکل فاکتورگیری شده می باشد که شما را قادر می سازد تا فوراً اطلاعات مورد نیازتان را شناسایی کنید. موقعیت های مختلف جبری به شکل های استاندارد مختلف نیاز پیدا می کند ـــ شکل صرفاً بستگی به این دارد که به چه چیزی در معادله نیاز دارید.
به عنوان مثال، اگر بخواهید معادلۀ \(x^2+10x-2y+23=0\) را به شکل استاندارد تبدیل کنید، طبق مراحل زیر که شامل روشی با نام کامل کردن مربع (completing the square) می باشد، عمل می کنید (در فصل 3 از روش کامل کردن مربع برای حل کردن معادلات درجه دوم استفاده کردیم):
-
معادله را با جملات \(x^2\) و \(x\) (یا جملات \(y^2\) و \(y\) ) در یک سمت، بازنویسی کنید و بقیۀ جملات را به سمت دیگر معادله ببرید.
$$
x^2+10x-2y+23=0 \\[2ex]
x^2+10x=2y-23
$$
-
عددی را به هر سمت از معادله بیفزایید تا آن سمت را که دارای جملۀ مربع می باشد به یک سه جمله ای مربع کامل (perfect square trinomial) تبدیل کنید. با این کار می توانید از روش کامل کردن مربع که در فصل 3 توضیح داده شده است، استفاده کنید.
$$
x^2+10x+25=2y-23+25 \\[2ex]
x^2+10x+25=2y+2
$$
-
سه جمله ای مربع کامل را در شکل فاکتورگیری شدۀ آن بازنویسی کنید، و جملات موجود در سمت دیگر معادله را با ضریب متغیر، فاکتورگیری نمایید.
$$ (x+5)^2=2(y+1) $$
اکنون این معادله را در شکل استاندارد آن در اختیار دارید. رأس آن در \((-5,-1)\) می باشد؛ رو به سمت بالا باز می شود و نسبتاً عریض می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: