خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
سری (series)
سری (series) مجموع چندین جمله در یک دنباله می باشد. چند جمله؟ خود این تعداد جملات بخشی از مسأله است ـــ تعداد جملات یا به شما داده می شود و یا اینکه خودتان برای پاسخ دادن به برخی سوالات، این تعداد را تعیین می کنید.

توانایی لیست کردنِ تمامی جملات یک دنباله یک ابزار مفید است که شما باید آن را بدانید، اما شما کارهای بیشتری را می توانید با دنباله ها انجام بدهید. به عنوان مثال، جمع زدن چندین جمله در یک دنباله در مواقعی که آن دنباله لیستی از کمک هزینه های دریافتی شما در طول این ماه باشد یا چند تا صندلی برای نشستن در تئاتر قرار دارد.
یافتنِ مجموع دنباله ها بدین معنا می باشد که به هر تعداد جمله که نیاز داشته باشید با یکدیگر جمع بزنید تا بدانید مجموع کمک هزینه های دریافتی این ماه شما چقدر است، یا بدانید چند نفر در \(20\) ردیف اول تئاتر نشسته اند. این فرآیند به نظر زیاد سخت و طاقت فرسا نمی رسد، مخصوصاً با ماشین حسابهای دستی، اما اگر اعداد واقعاً بزرگ باشند و شما بخواهید تعداد زیادی از آنها را با یکدیگر جمع بزنید، این فرآیند می تواند دلهره آور باشد.
به همین دلیل، بسیاری از دنباله ها که در کسب و کارها و برنامه های مالی مورد استفاده قرار می گیرند، دارای فرمولهایی برای مجموع جملاتشان می باشند. این فرمولها کمک بسیار بزرگی هستند. در واقع، برای برخی از سری های هندسی (geometric series)، شما می توانید تمامی جملات را ـــ تا ابد ـــ با یکدیگر جمع بزنید و قادر باشید تا مجموع تمامی جملات را پیش بینی کنید.
ریاضیدانان تمایل دارند تا فرمولها و قواعد را شسته و رفته و مختصر نگهدارند، بنابراین آنها نماد خاصی را برای نشان دادن اینکه شما مشغول جمع زدن جملات یک دنباله می باشید، ایجاد کرده اند. این نماد خاص سیگما (sigma) یا نماد جمع بندی (sum notation) نام دارد که آن را با \(\sum\) نشان می دهند.
در مثال زیر، شما می خواهید مجموع \(5\) جملۀ اول دنباله را بیابید، با قرار دادن \(k=1,2,3,4,5\) و جمع زدن جملات مربوطه به حاصلجمع می رسید:
$$
\sum_{k=1}^5 (k^2-2) \\[2ex]
\sum_{k=1}^5 (k^2-2) = (1^2-2)+(2^2-2)+(3^2-2)+(4^2-2)+(5^2-2) \\[2ex]
=-1+2+7+14+23=45
$$
شما دریافتید که مجموع این جملات \(45\) می باشد.
یک دنباله حسابی دارای یک قاعدۀ عمومی می باشد که شامل اولین جمله و تفاضل مشترک بین جملات متوالی می باشد: \(a_n=a_1+(n-1)d\) . یک سری حسابی (arithmetic series) مجموع جملات موجود در یک دنباله حسابی می باشد. دنبالۀ حسابیِ \(a_n=4+(n-1)5=5n-1\) را در نظر بگیرید. ده جملۀ اول در این دنباله عبارت از \(4, 9, 14, 19, 24, 29, 34, 39, 44, 49\) می باشند. مجموع این ده جمله برابر با \(265\) می شود. چطور به این عدد رسیدم؟ برای رسیدن به این عدد خیلی ساده این جملات را با یکدیگر جمع زدم. در مورد لیست های کوچک و اعداد کوچک، این روش بخوبی جواب می دهد. البته، همیشه اینطور نیست و برای راحتی در محاسبات بزرگتر فرمولی در این ارتباط وجود دارد که مجموع \(n\) جملۀ اول در یک دنبالۀ حسابی را محاسبه می کند.
در اینجا \(a_1\) جملۀ اول و \(d\) تفاضل مشترک از دنبالۀ حسابیِ \(a_n=a_1+(n-1)d\) می باشد. \(n\) تعیین می کند، کدام جمله از دنباله را می خواهید لحاظ بگیرید.
در مثال بعدی، \(n\) برابر با \(10\) می باشد، زیرا تعداد جملاتی که می خواهید با هم جمع بزنید ده تا هستند. با وارد کردن \(10\) به جای \(n\) در فرمولِ قاعدۀ کلیِ دنباله، به \(49\) می رسید.
برای استفاده از فرمول محاسبۀ مجموع جملات بر روی اعداد \(4, 9, 14, 19, 24, 29, 34,39, 44, 49\) ، داده های موجود را در فرمول قرار می دهید:
$$
S_n = {n \over 2}(a_1+a_n) \\[2ex]
S_{10}={10\over2}(4+49)=5(53)=265
$$
حالا فرض کنید می خواهید \(100\) عدد اول موجود در دنباله ای را که با عدد \(13\) آغاز می شود و دارای تفاضل مشترک \(2\) بین هر جمله می باشد، بدست آورید: \(13+15+17+19+...\) . شما می توانید مجموع این \(100\) عدد را با اولین بخش از فرمول مجموع دنباله های حسابی، به شکل زیر بیابید:
$$
S_n={n \over2}[2a_1+(n-1)d] \\[2ex]
S_{100} ={100 \over2}[2(13)+(100-1)2] = 50(26+198)=50(224)=11,200
$$
دنبالۀ هندسی عبارت از جملاتی می باشد که با یک نسبت عمومی، با هم متفاوتند. شما یک جمله در این دنباله را در یک عدد ثابت یا نسبت ضرب می کنید تا جملۀ بعدی را بیابید. برای یافتن مجموع جملات یک دنبالۀ هندسی می توانید از دو فرمول متفاوت استفاده کنید. از فرمول اول برای یافتن مجموع تعداد محدودی از جملات در یک دنبالۀ هندسی ـــ هر دنباله هندسی ـــ استفاده می کنید. فرمول دوم، تنها در مورد دنباله های هندسی بکار می رود که دارای نسبتی می باشند که بین صفر و یک قرار دارد (یعنی یک کسر سره)؛ شما از آن زمانی استفاده می کنید که بخواهید تمامی جملات موجود در یک دنباله ـــ برای همیشه و تا ابد ـــ را بدست آورید.
فرمولی که برای محاسبۀ مجموع جملات محدودی از یک دنبالۀ هندسی مورد استفاده قرار می دهید شامل یک کسر است که در آن نسبت ـــ یا توانی از نسبت ـــ را از \(1\) تفریق می کنید. شما نمی توانید این کسر را کاهش بدهید، پس چنین تلاشی نکنید. صرفاً به همان شکل که هست از آن استفاده کنید.
به عنوان مثال، فرض کنید می خواهید مجموع ده جملۀ اول از دنبالۀ هندسیِ \(\{1, 3, 9, 27, 81, ...\}\) را بدست آورید. شما از روی این دنباله در می یابید که جملۀ اول \(1\) و نسبت مشترکی که جملات در آن ضرب می گردند، برابر با \(3\) می باشد. این اطلاعات را در فرمول جایگذاری کنید:
$$
S_n=\frac{g_1(1-r^n)}{1-r} \\[2ex]
S_{10}=\frac{1(1-3^{10})}{1-3}=\frac{1-59,049}{-2}=\frac{-59,048}{-2}=29,524
$$
کاملاً عدد بزرگی است! همانطور که مشاهده می کنید استفاده از فرمول بسیار ساده تر از جمع زدن جملات در دنباله، \(1 + 3 + 9 + 27 + 81 + 243 + 729 + 2,187 + 6,561 + 19,683\)، می باشد. آیا اینطور نیست؟
دنباله های هندسی دارای یک نسبت یا مضرب هستند، که یک جمله را به جملۀ بعدی در صف تبدیل می کند. اگر عددی را در \(4\) ضرب کنید و نتیجۀ آن را نیز در \(4\) ضرب کنید و همینطور ادامه دهید، در زمان کوتاهی اعداد بسیار بزرگی خواهید ساخت. بنابراین، به نظر می رسد جمع زدن اعدادی که بی نهایت بزرگ می شوند، غیرممکن باشد.
اما جبر یک ویژگی واقعاً فوق العاده برای دنباله های هندسی که نسبت آنها بین \(-1\) و \(1\) باشد، دارد. مقادیر موجود در این دنباله ها کوچک و کوچکتر می شوند، و مجموع جملات موجود در این نوع دنباله ها هرگز از مقادیر ثابتی بالاتر نمی رود.
در شکل 1-16 ، شما جملاتی از یک دنباله را می بینید که با \(1\) آغاز شده است و دارای نسبت \({1\over2}\) می باشد. همچنین مجموع جملات تا هر جملۀ متوالی را می بینید.
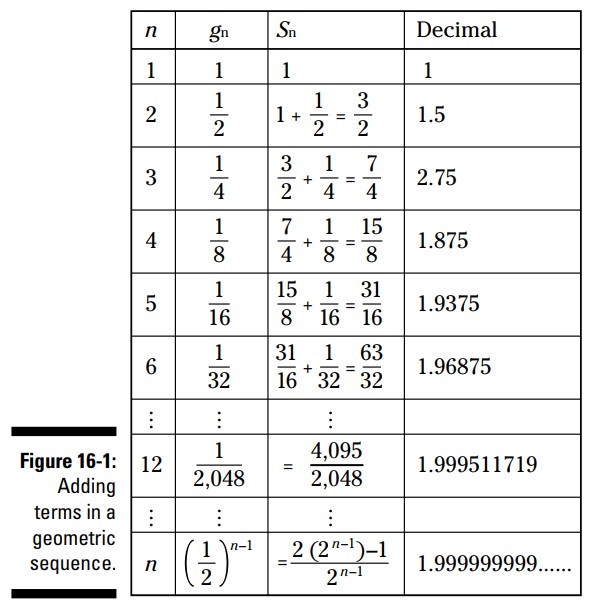
همانطور که در شکل 1-16 می بینید، مجموع این جملات، همینطور که تعداد جملات افزایش می یابند، تقریباً برابر با \(2\) می باشد. عدد موجود در صورت این کسر مجموع، همواره برابر با یک واحد کمتر از دوبرابر مخرج می باشد. این مجموع در شکل 1-16 به \(2\) نزدیک می شود اما هرگز واقعاً به آن نمی رسد. این عدد آنقدر به \(2\) نزدیک می شود که می توانید آن را به \(2\) گرد کنید. این فرآیند نزدیک شدن به مقداری خاص در مورد هر نوع دنبالۀ هندسی که دارای یک کسر سره (بین صفر و یک) باشد، صحیح است.
جبر همچنین برای یافتن مجموع تمامی جملات موجود در یک دنبالۀ هندسی با نسبتی بین صفر و یک، فرمولی را پیشنهاد می کند. شما ممکن است با خودتان فکر کنید که این فرمول از فرمول یافتن صرفاً چند جملۀ محدود پیچیده تر باشد، اما اینطور نیست. در واقع این فرمول بسیار ساده تر هم هست.
شما می توانید این قاعده را در مورد مجموع دنبالۀ مثال بالا که جملۀ آغازین آن \(1\) و نسبت مشترک آن \({1\over2}\) است، بکار ببرید:
$$ S_n \to \frac{g_1}{1-r}=\frac{1}{1-{1\over2}}=\frac{1}{{1\over2}}=2 $$

توانایی لیست کردنِ تمامی جملات یک دنباله یک ابزار مفید است که شما باید آن را بدانید، اما شما کارهای بیشتری را می توانید با دنباله ها انجام بدهید. به عنوان مثال، جمع زدن چندین جمله در یک دنباله در مواقعی که آن دنباله لیستی از کمک هزینه های دریافتی شما در طول این ماه باشد یا چند تا صندلی برای نشستن در تئاتر قرار دارد.
یافتنِ مجموع دنباله ها بدین معنا می باشد که به هر تعداد جمله که نیاز داشته باشید با یکدیگر جمع بزنید تا بدانید مجموع کمک هزینه های دریافتی این ماه شما چقدر است، یا بدانید چند نفر در \(20\) ردیف اول تئاتر نشسته اند. این فرآیند به نظر زیاد سخت و طاقت فرسا نمی رسد، مخصوصاً با ماشین حسابهای دستی، اما اگر اعداد واقعاً بزرگ باشند و شما بخواهید تعداد زیادی از آنها را با یکدیگر جمع بزنید، این فرآیند می تواند دلهره آور باشد.
به همین دلیل، بسیاری از دنباله ها که در کسب و کارها و برنامه های مالی مورد استفاده قرار می گیرند، دارای فرمولهایی برای مجموع جملاتشان می باشند. این فرمولها کمک بسیار بزرگی هستند. در واقع، برای برخی از سری های هندسی (geometric series)، شما می توانید تمامی جملات را ـــ تا ابد ـــ با یکدیگر جمع بزنید و قادر باشید تا مجموع تمامی جملات را پیش بینی کنید.
معرفی نماد جمع بندی (summation notation)
ریاضیدانان تمایل دارند تا فرمولها و قواعد را شسته و رفته و مختصر نگهدارند، بنابراین آنها نماد خاصی را برای نشان دادن اینکه شما مشغول جمع زدن جملات یک دنباله می باشید، ایجاد کرده اند. این نماد خاص سیگما (sigma) یا نماد جمع بندی (sum notation) نام دارد که آن را با \(\sum\) نشان می دهند.
قوانین جبر: نماد زیر نشان می دهد که شما می خواهید تمامی جملات را در دنباله ای که قاعدۀ کلی آن \(a_k\) می باشد، از\( k=1\) تا \(k=n\) با یکدیگر جمع بزنید:
$$
\sum_{k=1}^n k_a \\[2ex]
\sum_{k=1}^n k_a =a_1+a_2+a_3+a_4+...+a_{n-1}+a_n
$$
$$
\sum_{k=1}^n k_a \\[2ex]
\sum_{k=1}^n k_a =a_1+a_2+a_3+a_4+...+a_{n-1}+a_n
$$
در مثال زیر، شما می خواهید مجموع \(5\) جملۀ اول دنباله را بیابید، با قرار دادن \(k=1,2,3,4,5\) و جمع زدن جملات مربوطه به حاصلجمع می رسید:
$$
\sum_{k=1}^5 (k^2-2) \\[2ex]
\sum_{k=1}^5 (k^2-2) = (1^2-2)+(2^2-2)+(3^2-2)+(4^2-2)+(5^2-2) \\[2ex]
=-1+2+7+14+23=45
$$
شما دریافتید که مجموع این جملات \(45\) می باشد.
نکته: اگر بخواهید تمامی جملات یک دنباله را با هم جمع بزنید، برای همیشه و تا ابد، از نماد \(\infty\) در نماد سیگما به شکل زیر استفاده می کنید:
$$ \sum_{k=1}^{\infty} a_k $$
$$ \sum_{k=1}^{\infty} a_k $$
مجموع در دنباله های حسابی
یک دنباله حسابی دارای یک قاعدۀ عمومی می باشد که شامل اولین جمله و تفاضل مشترک بین جملات متوالی می باشد: \(a_n=a_1+(n-1)d\) . یک سری حسابی (arithmetic series) مجموع جملات موجود در یک دنباله حسابی می باشد. دنبالۀ حسابیِ \(a_n=4+(n-1)5=5n-1\) را در نظر بگیرید. ده جملۀ اول در این دنباله عبارت از \(4, 9, 14, 19, 24, 29, 34, 39, 44, 49\) می باشند. مجموع این ده جمله برابر با \(265\) می شود. چطور به این عدد رسیدم؟ برای رسیدن به این عدد خیلی ساده این جملات را با یکدیگر جمع زدم. در مورد لیست های کوچک و اعداد کوچک، این روش بخوبی جواب می دهد. البته، همیشه اینطور نیست و برای راحتی در محاسبات بزرگتر فرمولی در این ارتباط وجود دارد که مجموع \(n\) جملۀ اول در یک دنبالۀ حسابی را محاسبه می کند.
قوانین جبر: مجموع \(n\) جملۀ اول از یک دنبالۀ حسابی را با \(S_n\) نشان می دهند و از فرمول زیر بدست می آید:
$$ S_n={n \over 2}[2a_1+(n-1)d]={n \over 2}(a_1+a_n) $$
$$ S_n={n \over 2}[2a_1+(n-1)d]={n \over 2}(a_1+a_n) $$
در اینجا \(a_1\) جملۀ اول و \(d\) تفاضل مشترک از دنبالۀ حسابیِ \(a_n=a_1+(n-1)d\) می باشد. \(n\) تعیین می کند، کدام جمله از دنباله را می خواهید لحاظ بگیرید.
یادتان باشد: اولین بخش از این فرمول، درسمت چپ، به شما امکان می دهد تا اولین جمله، تفاضل مشترک، و تعداد جملاتی که می خواهید با هم جمع بزنید، را وارد نمایید. دومین بخش در سمت راست، سریعتر و ساده تر است؛ شما زمانی از آن استفاده می کنید که هر دو جملۀ اول و آخر را بدانید و همینطور تعداد جملاتی را که می خواهید با هم جمع بزنید، بدانید.
در مثال بعدی، \(n\) برابر با \(10\) می باشد، زیرا تعداد جملاتی که می خواهید با هم جمع بزنید ده تا هستند. با وارد کردن \(10\) به جای \(n\) در فرمولِ قاعدۀ کلیِ دنباله، به \(49\) می رسید.
برای استفاده از فرمول محاسبۀ مجموع جملات بر روی اعداد \(4, 9, 14, 19, 24, 29, 34,39, 44, 49\) ، داده های موجود را در فرمول قرار می دهید:
$$
S_n = {n \over 2}(a_1+a_n) \\[2ex]
S_{10}={10\over2}(4+49)=5(53)=265
$$
حالا فرض کنید می خواهید \(100\) عدد اول موجود در دنباله ای را که با عدد \(13\) آغاز می شود و دارای تفاضل مشترک \(2\) بین هر جمله می باشد، بدست آورید: \(13+15+17+19+...\) . شما می توانید مجموع این \(100\) عدد را با اولین بخش از فرمول مجموع دنباله های حسابی، به شکل زیر بیابید:
$$
S_n={n \over2}[2a_1+(n-1)d] \\[2ex]
S_{100} ={100 \over2}[2(13)+(100-1)2] = 50(26+198)=50(224)=11,200
$$
مجموع در دنباله های هندسی
دنبالۀ هندسی عبارت از جملاتی می باشد که با یک نسبت عمومی، با هم متفاوتند. شما یک جمله در این دنباله را در یک عدد ثابت یا نسبت ضرب می کنید تا جملۀ بعدی را بیابید. برای یافتن مجموع جملات یک دنبالۀ هندسی می توانید از دو فرمول متفاوت استفاده کنید. از فرمول اول برای یافتن مجموع تعداد محدودی از جملات در یک دنبالۀ هندسی ـــ هر دنباله هندسی ـــ استفاده می کنید. فرمول دوم، تنها در مورد دنباله های هندسی بکار می رود که دارای نسبتی می باشند که بین صفر و یک قرار دارد (یعنی یک کسر سره)؛ شما از آن زمانی استفاده می کنید که بخواهید تمامی جملات موجود در یک دنباله ـــ برای همیشه و تا ابد ـــ را بدست آورید.
محاسبۀ مجموع \(n\) جملۀ اول در دنبالۀ هندسی
فرمولی که برای محاسبۀ مجموع جملات محدودی از یک دنبالۀ هندسی مورد استفاده قرار می دهید شامل یک کسر است که در آن نسبت ـــ یا توانی از نسبت ـــ را از \(1\) تفریق می کنید. شما نمی توانید این کسر را کاهش بدهید، پس چنین تلاشی نکنید. صرفاً به همان شکل که هست از آن استفاده کنید.
قوانین جبر: شما می توانید مجموع \(n\) جملۀ اول از دنبالۀ هندسیِ \(g_n=g_1r^{n-1}\) را با فرمول زیر بیابید:
$$ S_n=\frac{g_1(1-r^n)}{1-r} $$
جملۀ \(g_1\) اولین جمله از دنباله است و \(r\) نشان دهندۀ نسبت مشترک می باشد.
$$ S_n=\frac{g_1(1-r^n)}{1-r} $$
جملۀ \(g_1\) اولین جمله از دنباله است و \(r\) نشان دهندۀ نسبت مشترک می باشد.
به عنوان مثال، فرض کنید می خواهید مجموع ده جملۀ اول از دنبالۀ هندسیِ \(\{1, 3, 9, 27, 81, ...\}\) را بدست آورید. شما از روی این دنباله در می یابید که جملۀ اول \(1\) و نسبت مشترکی که جملات در آن ضرب می گردند، برابر با \(3\) می باشد. این اطلاعات را در فرمول جایگذاری کنید:
$$
S_n=\frac{g_1(1-r^n)}{1-r} \\[2ex]
S_{10}=\frac{1(1-3^{10})}{1-3}=\frac{1-59,049}{-2}=\frac{-59,048}{-2}=29,524
$$
کاملاً عدد بزرگی است! همانطور که مشاهده می کنید استفاده از فرمول بسیار ساده تر از جمع زدن جملات در دنباله، \(1 + 3 + 9 + 27 + 81 + 243 + 729 + 2,187 + 6,561 + 19,683\)، می باشد. آیا اینطور نیست؟
محاسبۀ مجموع جملات یک دنبالۀ هندسی تا بی نهایت جمله
دنباله های هندسی دارای یک نسبت یا مضرب هستند، که یک جمله را به جملۀ بعدی در صف تبدیل می کند. اگر عددی را در \(4\) ضرب کنید و نتیجۀ آن را نیز در \(4\) ضرب کنید و همینطور ادامه دهید، در زمان کوتاهی اعداد بسیار بزرگی خواهید ساخت. بنابراین، به نظر می رسد جمع زدن اعدادی که بی نهایت بزرگ می شوند، غیرممکن باشد.
اما جبر یک ویژگی واقعاً فوق العاده برای دنباله های هندسی که نسبت آنها بین \(-1\) و \(1\) باشد، دارد. مقادیر موجود در این دنباله ها کوچک و کوچکتر می شوند، و مجموع جملات موجود در این نوع دنباله ها هرگز از مقادیر ثابتی بالاتر نمی رود.
نکات فنی: اگر نسبت بزرگتر از یک باشد، مجموع بزرگ و بزرگتر می گردد، و شما یک پاسخ نهایی نخواهید داشت. اگر نسبت منفی و مقداری بین \(0\) و \(-1\) باشد، مجموع یک مقدار ثابت خواهد بود. در مورد نسبت های کوچکتر از \(-1\) ، شما دوباره آشفتگی کامل خواهید داشت.
در شکل 1-16 ، شما جملاتی از یک دنباله را می بینید که با \(1\) آغاز شده است و دارای نسبت \({1\over2}\) می باشد. همچنین مجموع جملات تا هر جملۀ متوالی را می بینید.

قوانین جبر: قاعدۀ عمومی برای این دنباله به شرح زیر می باشد:
$$ g_n=g_1r^{n-1}=1 \cdot \biggl({1\over2}\biggr)^{n-1}=\biggl({1\over2}\biggr)^{n-1} $$
بنابراین، شما در واقع توانهایی از \({1\over2}\) را می یابید. در اینجا چندین جملۀ اول این دنباله را می بینید:
$$ \biggl \{1,{1\over2},{1\over4},{1\over8},{1\over16},{1\over32},{1\over64},{1\over128},{1\over256},{1\over512},... \biggr \} $$
$$ g_n=g_1r^{n-1}=1 \cdot \biggl({1\over2}\biggr)^{n-1}=\biggl({1\over2}\biggr)^{n-1} $$
بنابراین، شما در واقع توانهایی از \({1\over2}\) را می یابید. در اینجا چندین جملۀ اول این دنباله را می بینید:
$$ \biggl \{1,{1\over2},{1\over4},{1\over8},{1\over16},{1\over32},{1\over64},{1\over128},{1\over256},{1\over512},... \biggr \} $$
همانطور که در شکل 1-16 می بینید، مجموع این جملات، همینطور که تعداد جملات افزایش می یابند، تقریباً برابر با \(2\) می باشد. عدد موجود در صورت این کسر مجموع، همواره برابر با یک واحد کمتر از دوبرابر مخرج می باشد. این مجموع در شکل 1-16 به \(2\) نزدیک می شود اما هرگز واقعاً به آن نمی رسد. این عدد آنقدر به \(2\) نزدیک می شود که می توانید آن را به \(2\) گرد کنید. این فرآیند نزدیک شدن به مقداری خاص در مورد هر نوع دنبالۀ هندسی که دارای یک کسر سره (بین صفر و یک) باشد، صحیح است.
جبر همچنین برای یافتن مجموع تمامی جملات موجود در یک دنبالۀ هندسی با نسبتی بین صفر و یک، فرمولی را پیشنهاد می کند. شما ممکن است با خودتان فکر کنید که این فرمول از فرمول یافتن صرفاً چند جملۀ محدود پیچیده تر باشد، اما اینطور نیست. در واقع این فرمول بسیار ساده تر هم هست.
قوانین جبر: مجموع تمامی جملات یک دنبالۀ هندسی که نسبت \((r)\) آن بین صفر و یک می باشد \((0 \lt r \lt 1)\) برابر است با:
$$ S_n \to \frac{g_1}{1-r} $$
در این فرمول \(g_1\) اولین جمله در دنباله است.
$$ S_n \to \frac{g_1}{1-r} $$
در این فرمول \(g_1\) اولین جمله در دنباله است.
شما می توانید این قاعده را در مورد مجموع دنبالۀ مثال بالا که جملۀ آغازین آن \(1\) و نسبت مشترک آن \({1\over2}\) است، بکار ببرید:
$$ S_n \to \frac{g_1}{1-r}=\frac{1}{1-{1\over2}}=\frac{1}{{1\over2}}=2 $$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: