خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
نمودارهای ون (Venn diagrams)

نمودارهای ون (Venn diagrams) تصاویری هستند که ارتباط بین دو یا چند مجموعه و اعضاء آن مجموعه ها را نشان می دهند. ضرب المثل معروف "یک تصویر به اندازۀ هزار کلمه می ارزد" در مورد این نمودارها کاملاً صادق است. نمودارهای ون به شما کمک می کنند یک وضعیت را مرتب کنید و به یک نتیجه گیری برسید. بسیاری از مسأله هایی که شما با نمودارهای ون حل می کنید در پاراگراف ها آمده اند ـــ شامل کلمات و اعداد بسیار همراه با ارتباطات گیج کننده هستند. برچسب گذاری دایره ها در نمودار و پر کردن اعداد در آنها به شما کمک می کند مشخص سازید که چگونه همه چیز با هم کار می کنند ـــ و شما را قادر می سازد تا اگر چیزی را فراموش کرده باشید، آنرا ببینید.

به عنوان مثال، نمودار ون که در شکل 1-17 نشان داده شده است، مجموعۀ \(A\) را که شامل حروف کلمۀ encyclopedia می باشد، به شما نشان می دهد، و مجموعۀ \(B\) شامل حروف الفبایی می باشد که با کلمۀ see هم قافیه هستند. هر دوی این مجموعه ها با یک مجموعۀ مرجع محصور شده اند که شامل تمامی حروف الفبا است.
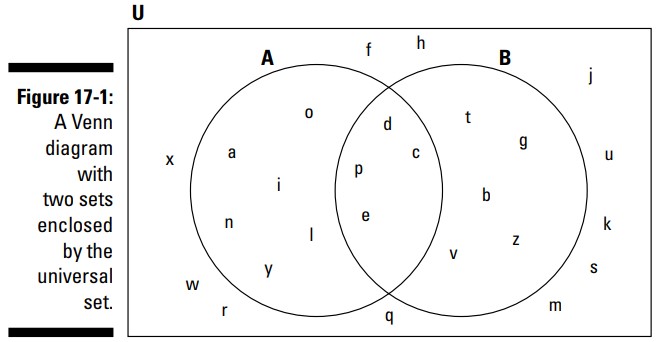
توجه داشته باشید که حروف c ، d ، e ، و p در هر دو مجموعه ظاهر شده اند. نمودار ون دانستن اینکه اعضا در کجا قرار دارند و دارای چه ویژگی هایی می باشند را ساده کرده است.
کار مرتب سازی حروف الفبا مبتنی بر محل قرار گیری آنها در یک کلمه یا اینکه این حروف با چه چیزی هم قافیه می باشند، که در مثال قبلی دیدید، ممکن است خیلی رضایتبخش نباشد. کاربردهای واقعی مجموعه ها اندکی پیچیده تر هستند، اما مثالهایی که در اینجا داریم، چیزهای اولیه و پایه ای را به شما نشان می دهند. برخی از کاربردهای واقعی نمودارهای ون در دنیای واقعی، شامل تبلیغات (نمودارهای انواع تبلیغات و نتایج آنها)، سیاست (فهمیدن اینکه چه کسی در مورد مسائل چه عقیده ای دارد و چگونه می خواهد از رأی هایش استفاده کند)، ژنتیک و پزشکی (بررسی ویژگیها و واکنش ها مبتنی بر علائم و نتایج)، و به همین ترتیب می باشند. مثال بعدی، در نسخه ای ساده سازی شده، چگونگی مفید بودن نمودارهای ون را نشان می دهد.
یک روزنامه محلی در شیکاگو با \(40\) نفر مصاحبه کرد تا تعیین کردن آیا آنها طرفدار تیم بیسیال Chicago White Sox هستند و/یا طرفدار تیم فوتبال Chicago Bears اند. از افراد مورد مصاحبه، \(25\) نفرشان طرفدار White Sox بودند، و \(9\) نفرشان هر دو تیم را دوست داشتند، و \(7\) نفر هم به هیچ کدام از این تیم ها اهمیتی نمی دادند. چند نفر طرفدار Bears هستند؟
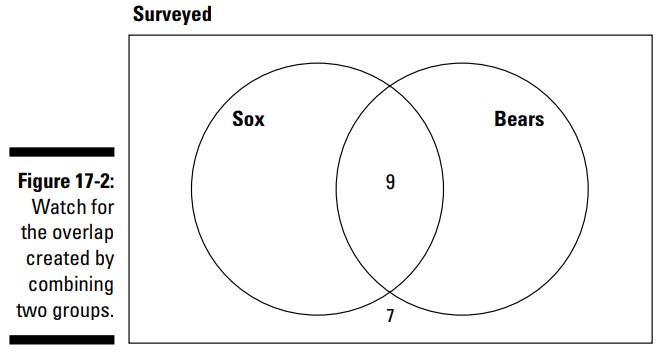
همانطور که می توانید ببینید، \(25+9+7=41\) ، که بیش از \(40\) فرد مصاحبه شونده می باشد. این فرآیند باید دارای برخی همپوشانی ها باشد. شما می توانید این همپوشانی ها را با یک نمودار ون نشان بدهید. شما یک دایره برای طرفداران White Sox ، یک دایره برای طرفداران Bears ، و یک مستطیل هم برای تمامی افراد مصاحبه شونده، می سازید. کار را با قرار دادن آن \(7\) نفر که هیچ کدام از تیم ها را دوست نداشتند، در قسمت بیرون دایره ها و در داخل مستطیل آغاز کنید. سپس آن \(9\) نفری را که هر دو تیم را دوست داشتند در قسمت مشترک دایره ها (محل تقاطعشان) قرار دهید. (شکل 2-17 را ببینید).
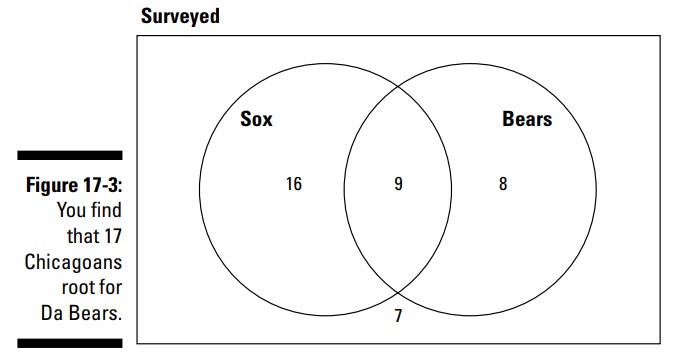
تعداد طرفدارن White Sox برابر با \(25\) نفر می باشد، بنابراین، اگر فقط \(16\) را در دایرۀ Sox قرار دهید، عدد موجود در کل دایره (شامل بخش همپوشانی شده) به \(25\) می رسد. تنها ناحیه باقیمانده در این دایره، جایی است که طرفدارن تیم Bears که طرفدار Sox نمی باشند، قرار دارند. تا اینجا، شما به مجموع \(25+7=32\) رسیده اید. بنابراین، شما می توانید بگویید که \(8\) نفر هستند که علاقمند Bears هستند و علاقه ای هم به Sox ندارند. شما \(8\) را در آن ناحیه قرار می دهید، و خواهید دید که مجموع طرفداران تیم Bears به \(17\) نفر می رسد (شکل 3-17 را ببینید).
هنگام حل کردن مسائل جبر، معمولاً مجبور می شوید تا از عملیات مجموعه ها شامل اجتماع، اشتراک، و متمم در ترکیبات مختلف استفاده کنید. در اینگونه وضعیتها، نمودارهای ون برای مرتب سازی برخی از انواع گزاره های پیچیده، سودمند می باشند.
به عنوان مثال، آیا این گزاره صحیح است: \((C \cup D)' = C' \cap D'\) (به این شکل خوانده می شود که متمم اجتماعِ \(C\) و \(D\) برابر است با اشتراک متمم \(C\) و متمم \(D\) ) ؟ شما می توانید هر کدام از این وضعیتها را ترسیم کنید تا آنها را با استفاده از نمودارهای ون مقایسه کنید. شما از سایه گذاری برای تعیین بخشهای مختلف گزاره استفاده می کنید.
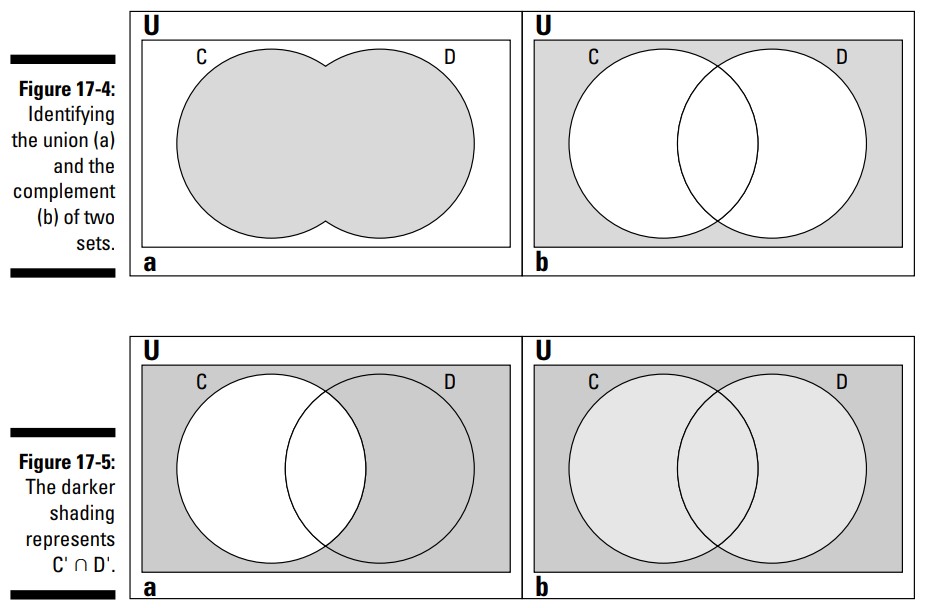
در بخش a از شکل 4-17 شما \(C \cup D\) را می بینید که سایه گذاری شده است ـــ تمامی اعضائی که هم در \(C\) و هم در \(D\) ظاهر شده اند. در بخش b از شکل 4-17 شما \((C \cup D)'\) را می بینید که سایه دار شده است. متمم نشان دهندۀ تمامی اعضائی است که در این مجموعه مشخص نشده اند (اما در مجموعۀ مرجع وجود دارند)، بنابراین مشابه نگاتیو یک عکس می باشد ـــ تمامی نواحی متضاد آن سایه دار شده اند.
اکنون می توانید با نیمۀ دیگر معادله درگیر شوید. ابتدا، در بخش a از شکل 5-17 شما \(C'\) را می بینید که سایه خورده است. ناحیۀ سایه دار شده نشان دهندۀ تمامی اعضایی می باشد که در \(C\) نیستند. در بخش b از شکل 5-17 هم \(C'\) و هم \(D'\) را می بینید که سایه خورده اند، و اشتراک آنها (اعضاء مشترک بین این دو) با سایۀ تیره تری مشخص شده است تا محل همپوشانی آنها را نشان دهد. آیا این همپوشانی با طرح \((C \cup D)'\) مطابقت دارد؟ بله، بخش b از شکل 4-17 و بخش b از شکل 5-17 یکسان هستند ـــ ناحیه های یکسانی در آنها سایه دار شده اند، بنابراین شما این معادله را تصدیق می کنید.
این نمودار ون نشان می دهد که دو گزارۀ کاملاً متفاوت می توانند یکسان باشند. کار کردن با مجموعه ها و عملیات مجموعه ها به لحاظ جبری، مشکل می باشد، به همین دلیل هم هست که استفاده از یک رویکرد تصویری مانند نمودارهای ون، برای نشان دادن یا اثبات اینکه یک معادله یا گزارۀ دیگری صحیح می باشد، موفق عمل می کنند. استفاده از نمودارهای ون برای تفکیک گزاره های مرکب به شما یک تایید بصری و دقیق را می دهد.
نشان دادن ارتباط بین اعضای دو مجموعه با یک نمودار ون کاملاً سرراست است. اما، مانند بیشتر فرآیندهای ریاضی، شما می توانید نمودار را یک مرحله جلوتر ببرید تا ارتباط بین سه مجموعه را نشان دهید. شما همچنین می توانید چهار مجموعه را مدیریت کنید، اما نمودار کاملاً پیچیده می شود و بدلیل روشی که شما باید شکل را ترسیم کنید، آنقدرها مفید نخواهد بود.
هنگامی که دو مجموعه همپوشانی دارند، شما تصویر را به چهار ناحیۀ مجزا تقسیم می کنید: خارج از دو دایره، همپوشانی دایره ها، و دو بخشی که همپوشانی ندارند اما در یک دایره یا دایرۀ دیگر ظاهر شده اند. هنگامی که سه دایره را با همپوشانی در یک نمودار ون نشان می دهید، شما هشت ناحیۀ مجزا را می سازید. شکل 6-17 چگونگی تکمیل این فرآیند را به شما نشان می دهد.
شما می توانید این هشت ناحیه را که با تقاطع سه دایره با یکدیگر بوجود آمده اند، به شرح زیر، توصیف کنید:
شما ممکن است مجبور شوید از یک سازماندهی مشابه این استفاده کنید تا اطلاعات را مرتب سازی کرده و به سوالات پاسخ دهید. به عنوان مثال، فرض کنید یک باشگاه با \(25\) عضو تصمیم گرفته است تا برای ملاقات بعدیشان پیتزا سفارش بدهد؛ منشی یک نظرسنجی می گیرد تا بداند هر شخصی چه چیزی را دوست دارد:
سوال اصلی اینست: چندنفر هیچکدام از این سه مادۀ غذایی را بر روی پیتزایشان دوست ندارند؟
همانطور که می بینید، مجموع اولویتها بیش از \(25\) می شود، بنابراین شما قطعاً باید همپوشانی هایی داشته باشید. شما می توانید با ترسیم سه دایرۀ متقاطع، و برچسب گذاری آنها با اسامی سوسیس (Sausage)، پپرونی (Pepperoni)، و قارچ (Mushrooms)، و پر کردن اعداد در آنها، به این سوال پاسخ دهید. برای پر کردن اعداد از آخرین مورد موجود در لیست استفاده کنید. بخش a از شکل 7-17 نمودار ون اولیه را که می توانید مورد استفاده قرار دهید، به شما نشان می دهد.

شما آن \(4\) نفری را که همۀ این سه نوع مادۀ غذایی را دوست دارند در بخش میانی نمودار قرار می دهید. هفت نفر هم پپرونی و هم قارچ دوست دارند، اما در حال حاضر شما فقط چهار تا از آنها را در وسط آورده اید، بنابراین عدد \(3\) را در ناحیۀ پپرونی و قارچ قرار دهید، اما در ناحیۀ سوسیس نباشد. ده نفر هم سوسیس و هم قارچ دوست دارند، اما شما در حال حاضر فقط چهار تا از آنها را در ناحیۀ میانی ذکر کرده اید، بنابراین عدد \(6\) را در ناحیۀ سوسیس و قارچ قرار دهید، اما در ناحیۀ پپرونی نباشد. پنج نفر هم سوسیس و هم پپرونی دوست دارند، اما شما در حال حاضر چهار تا از آنها را به حساب آورده اید؛ در ناحیۀ سوسیس و پپرونی عدد \(1\) را قرار دهید، اما نه در ناحیۀ قارچ. بخش b از شکل 7-17 تمامی این مقادیر ورودی را به شما نشان می دهد.
اکنون می توانید بقیۀ نواحی دایره ها را پر کنید. سیزده نفر فقط قارچ دوست دارند، و شما هم اکنون در آن دایره \(13\) نفر را دارید، بنابراین در ناحیه افرادی که فقط قارچ دوست دارند \(0\) را قرار دهید. ده نفر فقط پپرونی دوست دارند؛ شما هم اکنون \(8\) نفر از آنها را در دایره دارید، بنابراین عدد \(2\) را برای ناحیۀ فقط پپرونی وارد کنید. چهارده نفر فقط سوسیس دوست دارند، بنابراین با احتساب بقیۀ موارد صرفاً عدد \(3\) را در ناحیۀ فقط سوسیس وارد کنید. در بخش c از شکل 7-17 می توانید تمامی این مقادیر وارد شده را ببینید.
شما با وارد کردن تمامی اعداد در بخش c از شکل 7-17 کار را تمام کرده اید. مجموع این اعداد \(19\) نفر می شود. این باشگاه \(25\) عضو دارد، بنابراین شما می توانید نتیجه بگیرید که \(6\) نفر از آنها نه سوسیس، نه قارچ، و نه پپرونی، هیچکدام از اینها را دوست ندارند. شما می توانید برای این افراد خاص و بدغذا فقط پیتزای پنیر ساده سفارش بدهید!

یادتان باشد: شما اغلب نمودارهای ون را با دایره های متقاطع ترسیم می کنید. شما این دایره ها را با اسامی مجموعه ها برچسب گذاری می کنید، و این دایره ها را با یک مجموعۀ مرجع محصور می کنید (یک مستطیل که دور همه دایره ها کشیده می شود). اعضای مشترک مجموعه ها در بخش های روی هم افتادۀ دایره های مربوطه با یکدیگر به اشتراک گذارده می شوند.
به عنوان مثال، نمودار ون که در شکل 1-17 نشان داده شده است، مجموعۀ \(A\) را که شامل حروف کلمۀ encyclopedia می باشد، به شما نشان می دهد، و مجموعۀ \(B\) شامل حروف الفبایی می باشد که با کلمۀ see هم قافیه هستند. هر دوی این مجموعه ها با یک مجموعۀ مرجع محصور شده اند که شامل تمامی حروف الفبا است.

توجه داشته باشید که حروف c ، d ، e ، و p در هر دو مجموعه ظاهر شده اند. نمودار ون دانستن اینکه اعضا در کجا قرار دارند و دارای چه ویژگی هایی می باشند را ساده کرده است.
به کار بردن نمودار ون
کار مرتب سازی حروف الفبا مبتنی بر محل قرار گیری آنها در یک کلمه یا اینکه این حروف با چه چیزی هم قافیه می باشند، که در مثال قبلی دیدید، ممکن است خیلی رضایتبخش نباشد. کاربردهای واقعی مجموعه ها اندکی پیچیده تر هستند، اما مثالهایی که در اینجا داریم، چیزهای اولیه و پایه ای را به شما نشان می دهند. برخی از کاربردهای واقعی نمودارهای ون در دنیای واقعی، شامل تبلیغات (نمودارهای انواع تبلیغات و نتایج آنها)، سیاست (فهمیدن اینکه چه کسی در مورد مسائل چه عقیده ای دارد و چگونه می خواهد از رأی هایش استفاده کند)، ژنتیک و پزشکی (بررسی ویژگیها و واکنش ها مبتنی بر علائم و نتایج)، و به همین ترتیب می باشند. مثال بعدی، در نسخه ای ساده سازی شده، چگونگی مفید بودن نمودارهای ون را نشان می دهد.
یک روزنامه محلی در شیکاگو با \(40\) نفر مصاحبه کرد تا تعیین کردن آیا آنها طرفدار تیم بیسیال Chicago White Sox هستند و/یا طرفدار تیم فوتبال Chicago Bears اند. از افراد مورد مصاحبه، \(25\) نفرشان طرفدار White Sox بودند، و \(9\) نفرشان هر دو تیم را دوست داشتند، و \(7\) نفر هم به هیچ کدام از این تیم ها اهمیتی نمی دادند. چند نفر طرفدار Bears هستند؟
همانطور که می توانید ببینید، \(25+9+7=41\) ، که بیش از \(40\) فرد مصاحبه شونده می باشد. این فرآیند باید دارای برخی همپوشانی ها باشد. شما می توانید این همپوشانی ها را با یک نمودار ون نشان بدهید. شما یک دایره برای طرفداران White Sox ، یک دایره برای طرفداران Bears ، و یک مستطیل هم برای تمامی افراد مصاحبه شونده، می سازید. کار را با قرار دادن آن \(7\) نفر که هیچ کدام از تیم ها را دوست نداشتند، در قسمت بیرون دایره ها و در داخل مستطیل آغاز کنید. سپس آن \(9\) نفری را که هر دو تیم را دوست داشتند در قسمت مشترک دایره ها (محل تقاطعشان) قرار دهید. (شکل 2-17 را ببینید).

تعداد طرفدارن White Sox برابر با \(25\) نفر می باشد، بنابراین، اگر فقط \(16\) را در دایرۀ Sox قرار دهید، عدد موجود در کل دایره (شامل بخش همپوشانی شده) به \(25\) می رسد. تنها ناحیه باقیمانده در این دایره، جایی است که طرفدارن تیم Bears که طرفدار Sox نمی باشند، قرار دارند. تا اینجا، شما به مجموع \(25+7=32\) رسیده اید. بنابراین، شما می توانید بگویید که \(8\) نفر هستند که علاقمند Bears هستند و علاقه ای هم به Sox ندارند. شما \(8\) را در آن ناحیه قرار می دهید، و خواهید دید که مجموع طرفداران تیم Bears به \(17\) نفر می رسد (شکل 3-17 را ببینید).

استفاده از نمودارهای ون همراه با عملیات مجموعه ها
هنگام حل کردن مسائل جبر، معمولاً مجبور می شوید تا از عملیات مجموعه ها شامل اجتماع، اشتراک، و متمم در ترکیبات مختلف استفاده کنید. در اینگونه وضعیتها، نمودارهای ون برای مرتب سازی برخی از انواع گزاره های پیچیده، سودمند می باشند.
به عنوان مثال، آیا این گزاره صحیح است: \((C \cup D)' = C' \cap D'\) (به این شکل خوانده می شود که متمم اجتماعِ \(C\) و \(D\) برابر است با اشتراک متمم \(C\) و متمم \(D\) ) ؟ شما می توانید هر کدام از این وضعیتها را ترسیم کنید تا آنها را با استفاده از نمودارهای ون مقایسه کنید. شما از سایه گذاری برای تعیین بخشهای مختلف گزاره استفاده می کنید.
در بخش a از شکل 4-17 شما \(C \cup D\) را می بینید که سایه گذاری شده است ـــ تمامی اعضائی که هم در \(C\) و هم در \(D\) ظاهر شده اند. در بخش b از شکل 4-17 شما \((C \cup D)'\) را می بینید که سایه دار شده است. متمم نشان دهندۀ تمامی اعضائی است که در این مجموعه مشخص نشده اند (اما در مجموعۀ مرجع وجود دارند)، بنابراین مشابه نگاتیو یک عکس می باشد ـــ تمامی نواحی متضاد آن سایه دار شده اند.
اکنون می توانید با نیمۀ دیگر معادله درگیر شوید. ابتدا، در بخش a از شکل 5-17 شما \(C'\) را می بینید که سایه خورده است. ناحیۀ سایه دار شده نشان دهندۀ تمامی اعضایی می باشد که در \(C\) نیستند. در بخش b از شکل 5-17 هم \(C'\) و هم \(D'\) را می بینید که سایه خورده اند، و اشتراک آنها (اعضاء مشترک بین این دو) با سایۀ تیره تری مشخص شده است تا محل همپوشانی آنها را نشان دهد. آیا این همپوشانی با طرح \((C \cup D)'\) مطابقت دارد؟ بله، بخش b از شکل 4-17 و بخش b از شکل 5-17 یکسان هستند ـــ ناحیه های یکسانی در آنها سایه دار شده اند، بنابراین شما این معادله را تصدیق می کنید.

این نمودار ون نشان می دهد که دو گزارۀ کاملاً متفاوت می توانند یکسان باشند. کار کردن با مجموعه ها و عملیات مجموعه ها به لحاظ جبری، مشکل می باشد، به همین دلیل هم هست که استفاده از یک رویکرد تصویری مانند نمودارهای ون، برای نشان دادن یا اثبات اینکه یک معادله یا گزارۀ دیگری صحیح می باشد، موفق عمل می کنند. استفاده از نمودارهای ون برای تفکیک گزاره های مرکب به شما یک تایید بصری و دقیق را می دهد.
نمایش بیش از دو مجموعه با نمودار ون
نشان دادن ارتباط بین اعضای دو مجموعه با یک نمودار ون کاملاً سرراست است. اما، مانند بیشتر فرآیندهای ریاضی، شما می توانید نمودار را یک مرحله جلوتر ببرید تا ارتباط بین سه مجموعه را نشان دهید. شما همچنین می توانید چهار مجموعه را مدیریت کنید، اما نمودار کاملاً پیچیده می شود و بدلیل روشی که شما باید شکل را ترسیم کنید، آنقدرها مفید نخواهد بود.
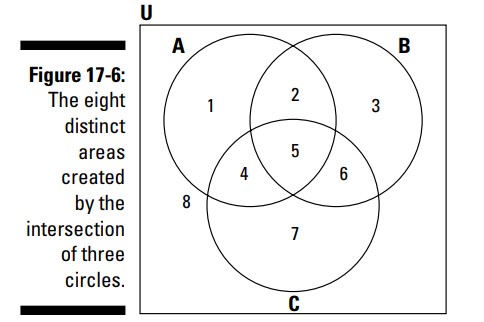
هنگامی که دو مجموعه همپوشانی دارند، شما تصویر را به چهار ناحیۀ مجزا تقسیم می کنید: خارج از دو دایره، همپوشانی دایره ها، و دو بخشی که همپوشانی ندارند اما در یک دایره یا دایرۀ دیگر ظاهر شده اند. هنگامی که سه دایره را با همپوشانی در یک نمودار ون نشان می دهید، شما هشت ناحیۀ مجزا را می سازید. شکل 6-17 چگونگی تکمیل این فرآیند را به شما نشان می دهد.

شما می توانید این هشت ناحیه را که با تقاطع سه دایره با یکدیگر بوجود آمده اند، به شرح زیر، توصیف کنید:
-
تمامی اعضایی که فقط در \(A\) هستند.
-
تمامی اعضای مشترک بین \(A\) و \(B\) که در \(C\) نیستند.
-
تمامی اعضایی که فقط در \(B\) هستند.
-
تمامی اعضای مشترک بین \(A\) و \(C\) که در \(B\) نیستند.
-
تمامی اعضای مشترک بین \(A\) ، \(B\) ، و \(C\) .
-
تمامی اعضای مشترک بین \(B\) و \(C\) که در \(A\) نیستند.
-
تمامی اعضایی که فقط در \(C\) هستند.
-
تمامی اعضایی که در \(A\) ، \(B\) ، و \(C\) قرار ندارند.
شما ممکن است مجبور شوید از یک سازماندهی مشابه این استفاده کنید تا اطلاعات را مرتب سازی کرده و به سوالات پاسخ دهید. به عنوان مثال، فرض کنید یک باشگاه با \(25\) عضو تصمیم گرفته است تا برای ملاقات بعدیشان پیتزا سفارش بدهد؛ منشی یک نظرسنجی می گیرد تا بداند هر شخصی چه چیزی را دوست دارد:
-
\(14\) نفر سوسیس دوست دارند.
-
\(10\) نفر پپرونی دوست دارند.
-
\(13\) نفر قارچ دوست دارند.
-
\(5\) نفر هم سوسیس و هم پپرونی دوست دارند.
-
\(10\) نفر هم سوسیس و هم قارچ دوست دارند.
-
\(7\) نفر هم پپرونی و هم قارچ دوست دارند.
-
\(4\) نفر هر سۀ این مواد غذایی را دوست دارند.
سوال اصلی اینست: چندنفر هیچکدام از این سه مادۀ غذایی را بر روی پیتزایشان دوست ندارند؟
همانطور که می بینید، مجموع اولویتها بیش از \(25\) می شود، بنابراین شما قطعاً باید همپوشانی هایی داشته باشید. شما می توانید با ترسیم سه دایرۀ متقاطع، و برچسب گذاری آنها با اسامی سوسیس (Sausage)، پپرونی (Pepperoni)، و قارچ (Mushrooms)، و پر کردن اعداد در آنها، به این سوال پاسخ دهید. برای پر کردن اعداد از آخرین مورد موجود در لیست استفاده کنید. بخش a از شکل 7-17 نمودار ون اولیه را که می توانید مورد استفاده قرار دهید، به شما نشان می دهد.

شما آن \(4\) نفری را که همۀ این سه نوع مادۀ غذایی را دوست دارند در بخش میانی نمودار قرار می دهید. هفت نفر هم پپرونی و هم قارچ دوست دارند، اما در حال حاضر شما فقط چهار تا از آنها را در وسط آورده اید، بنابراین عدد \(3\) را در ناحیۀ پپرونی و قارچ قرار دهید، اما در ناحیۀ سوسیس نباشد. ده نفر هم سوسیس و هم قارچ دوست دارند، اما شما در حال حاضر فقط چهار تا از آنها را در ناحیۀ میانی ذکر کرده اید، بنابراین عدد \(6\) را در ناحیۀ سوسیس و قارچ قرار دهید، اما در ناحیۀ پپرونی نباشد. پنج نفر هم سوسیس و هم پپرونی دوست دارند، اما شما در حال حاضر چهار تا از آنها را به حساب آورده اید؛ در ناحیۀ سوسیس و پپرونی عدد \(1\) را قرار دهید، اما نه در ناحیۀ قارچ. بخش b از شکل 7-17 تمامی این مقادیر ورودی را به شما نشان می دهد.
اکنون می توانید بقیۀ نواحی دایره ها را پر کنید. سیزده نفر فقط قارچ دوست دارند، و شما هم اکنون در آن دایره \(13\) نفر را دارید، بنابراین در ناحیه افرادی که فقط قارچ دوست دارند \(0\) را قرار دهید. ده نفر فقط پپرونی دوست دارند؛ شما هم اکنون \(8\) نفر از آنها را در دایره دارید، بنابراین عدد \(2\) را برای ناحیۀ فقط پپرونی وارد کنید. چهارده نفر فقط سوسیس دوست دارند، بنابراین با احتساب بقیۀ موارد صرفاً عدد \(3\) را در ناحیۀ فقط سوسیس وارد کنید. در بخش c از شکل 7-17 می توانید تمامی این مقادیر وارد شده را ببینید.
شما با وارد کردن تمامی اعداد در بخش c از شکل 7-17 کار را تمام کرده اید. مجموع این اعداد \(19\) نفر می شود. این باشگاه \(25\) عضو دارد، بنابراین شما می توانید نتیجه بگیرید که \(6\) نفر از آنها نه سوسیس، نه قارچ، و نه پپرونی، هیچکدام از اینها را دوست ندارند. شما می توانید برای این افراد خاص و بدغذا فقط پیتزای پنیر ساده سفارش بدهید!
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: