خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
نمودار درختی (tree diagram)
ترکیبات و جایگشت ها به شما می گویند که در داخل مجموعه های تعیین شده، انتظار چند زیرمجموعه یا گروه بندی را داشته باشیم، اما در مورد اینکه در آن گروه بندی ها یا زیرمجموعه ها، چه اعضایی قرار دارند، شما را راهنمایی نمی کنند. یک روش زیبا و منظم برای نوشتن تمامی ترکیبات یا جایگشت ها اینست که از یک نمودار درختی (tree diagram) استفاده کنید. نام نمودار درختی از این واقعیت می آید که طرح آن چیزی شبیه شجره نامه می باشد ـــ از سمت چپ به راست شاخه می زند. ورودیهایی که در منتهی الیه سمت چپ قرار دارند، اولین انتخابهای شما می باشند، ورودیهای ستون بعدی، چیزهایی هستند که بعد از آنها می توانید انتخاب کنید، و به همین ترتیب.

شما نمی توانید از نمودار درختی در تمامی وضعیتهایی که با جایگشت ها و ترکیبات درگیر هستند، استفاده کنید ـــ نمودارها بسیار بزرگ می شوند و همه جا گسترش می یابند ـــ اما در بسیاری از موقعیتها که با شمارش آیتم ها درگیر هستند، می توانند از آنها استفاده کنید. همچنین، نمودارهای درختی در دنیای آمار (statistics)، ژنتیک (genetics)، و سایر مطالعات، ظاهر می شوند.
هنگامی که دو حرف الفبای مختلف را از یک مجموعۀ چهار حرفی انتخاب می کنید، تا کلمات مختلفی را شکل دهید، می توانید تعداد کلمات ممکنِ مختلف را با جایگشت بیابید:
$$
\require{cancel}
_4P_2=\frac{4!}{(4-2)!}=\frac{4 \cdot 3 \cdot \cancel{2} \cdot \cancel{1}}{\cancel{2} \cdot \cancel{1}}=12 $$
شما می توانید \(12\) کلمۀ دو حرفی مختلف را بسازید. برای ایجاد لیستی از کلمات ـــ و جلوگیری از ذکر موارد تکراری یا از قلم انداختن موارد ـــ شما باید یک نمودار درختی بسازید.
این مراحل ساده را دنبال کنید:
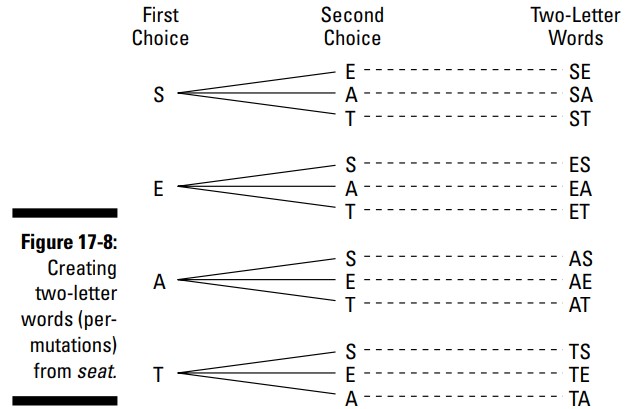
به عنوان مثال، فرض کنید که می خواهید با حروف کلمۀ seat جایگشت هایی را بسازید. شکل 8-17 نمودار درختی که این جایگشت ها را سازماندهی می کند، به شما نشان می دهد.
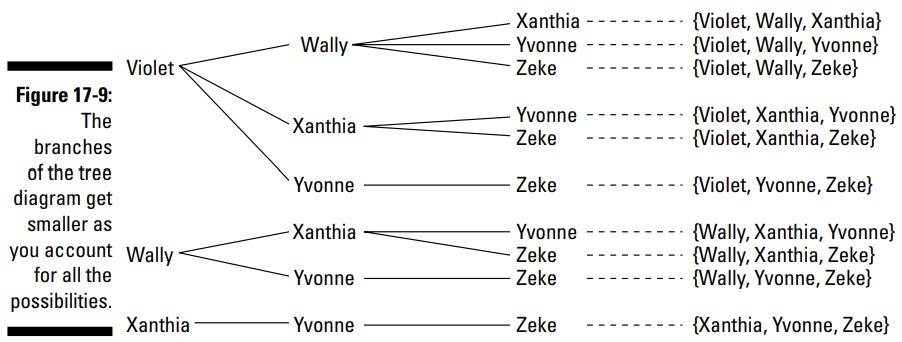
در بخش مربوط به آموزش ترکیب در همین فصل، مثالی برای شما زدیم که در آن سه دوست را از بین پنج دوست جهت همراهی شما در تئاتر انتخاب می کردید، و شما دریافتید که ده روش مختلف برای انتخاب آنها دارید. ترتیب این انتخابها مهم نیستند؛ آنها می توانند بیایند یا نه. نمودار درختی موجود در شکل 9-17 به شما نشان می دهد که چگونه تمام این سازماندهیها را بدون تکرار خودتان تعیین می کنید.
از آنجا که ترتیب اهمیتی ندارد، شما ابتدا تمامی چینش ها را با Violet و Wally می یابید، و سپس Violet و Xanthia ، و سپس Violet و Yvonne . تعداد شاخه ها مدام کاهش می یابند، زیرا شما گروه های تکراری را ذکر نمی کنید. سپس به سراغ Wally و Xanthia و سپس Wally و Yvonne می روید. در نهایت به سراغ Xanthia و می روید و همانجا متوقف می شوید، زیرا شما همۀ گروه بندی ها را لحاظ کرده اید.
شما ممکن است با خودتان بیندیشید که Violet شانس بیشتری برای انتخاب شدن داشته باشد، اما اینطور نیست. اگر هر ده مجموعه را با دقت بررسی کنید خواهید دید که هر شخص شش مرتبه در گروه بندیها ظاهر شده است.

شما نمی توانید از نمودار درختی در تمامی وضعیتهایی که با جایگشت ها و ترکیبات درگیر هستند، استفاده کنید ـــ نمودارها بسیار بزرگ می شوند و همه جا گسترش می یابند ـــ اما در بسیاری از موقعیتها که با شمارش آیتم ها درگیر هستند، می توانند از آنها استفاده کنید. همچنین، نمودارهای درختی در دنیای آمار (statistics)، ژنتیک (genetics)، و سایر مطالعات، ظاهر می شوند.
کشیدن نمودار درختی برای یک جایگشت
هنگامی که دو حرف الفبای مختلف را از یک مجموعۀ چهار حرفی انتخاب می کنید، تا کلمات مختلفی را شکل دهید، می توانید تعداد کلمات ممکنِ مختلف را با جایگشت بیابید:
$$
\require{cancel}
_4P_2=\frac{4!}{(4-2)!}=\frac{4 \cdot 3 \cdot \cancel{2} \cdot \cancel{1}}{\cancel{2} \cdot \cancel{1}}=12 $$
شما می توانید \(12\) کلمۀ دو حرفی مختلف را بسازید. برای ایجاد لیستی از کلمات ـــ و جلوگیری از ذکر موارد تکراری یا از قلم انداختن موارد ـــ شما باید یک نمودار درختی بسازید.
این مراحل ساده را دنبال کنید:
-
با تعدادی از آیتم های تعیین شده و لیست کردن آنها به صورت عمودی، کار را آغاز کنید ـــ یکی زیر دیگری ـــ فضایی را برای رشد درختتان در سمت راست خالی نگهدارید.
-
با کشیدن پاره خط های کوتاه، مجموعۀ ورودیهای بعدی را به مجموعۀ اول متصل سازید ـــ شاخه ها.
-
تا زمانیکه کار را تکمیل کنید به متصل کردن ورودیهای بیشتر به هر تعداد که مورد نیاز باشد، ادامه بدهید.
به عنوان مثال، فرض کنید که می خواهید با حروف کلمۀ seat جایگشت هایی را بسازید. شکل 8-17 نمودار درختی که این جایگشت ها را سازماندهی می کند، به شما نشان می دهد.

کشیدن نمودار درختی برای یک ترکیب
در بخش مربوط به آموزش ترکیب در همین فصل، مثالی برای شما زدیم که در آن سه دوست را از بین پنج دوست جهت همراهی شما در تئاتر انتخاب می کردید، و شما دریافتید که ده روش مختلف برای انتخاب آنها دارید. ترتیب این انتخابها مهم نیستند؛ آنها می توانند بیایند یا نه. نمودار درختی موجود در شکل 9-17 به شما نشان می دهد که چگونه تمام این سازماندهیها را بدون تکرار خودتان تعیین می کنید.
یادتان باشد: شما سازماندهی های (چینش ها) مختلف را با هر سه شخصی که بخواهید آغاز می کنید. اگر نمودار درختی تان را به درستی ترسیم کنید، مهم نیست که با چه اشخاصی شروع کرده اید ـــ شما به تعداد یکسانی گروه بندی همراه با ترکیبات یکسانی از اشخاص در گروه بندی ها می رسید.
از آنجا که ترتیب اهمیتی ندارد، شما ابتدا تمامی چینش ها را با Violet و Wally می یابید، و سپس Violet و Xanthia ، و سپس Violet و Yvonne . تعداد شاخه ها مدام کاهش می یابند، زیرا شما گروه های تکراری را ذکر نمی کنید. سپس به سراغ Wally و Xanthia و سپس Wally و Yvonne می روید. در نهایت به سراغ Xanthia و می روید و همانجا متوقف می شوید، زیرا شما همۀ گروه بندی ها را لحاظ کرده اید.

شما ممکن است با خودتان بیندیشید که Violet شانس بیشتری برای انتخاب شدن داشته باشد، اما اینطور نیست. اگر هر ده مجموعه را با دقت بررسی کنید خواهید دید که هر شخص شش مرتبه در گروه بندیها ظاهر شده است.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: