خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ده نوع خاص از اعداد
ریاضیدانان اعداد را به روش های بسیاری دسته بندی می کنند، درست شبیه روانشناسان (و خبرچین ها) که مردم را دسته بندی می کنند: زوج یا فرد، مثبت یا منفی، گویا یا اصم، و به همین ترتیب. در این فصل، شما با قرار دادن اعداد در گروههای جذاب که منجر می شود خاص گردند، روش های بیشتری را برای دسته بندی اعداد خواهید یافت.

اعداد مثلثی (Triangular numbers) اعدادی هستند که در دنبالۀ \(1, 3, 6, 10, 15, 21, 28, ...\) قرار دارند (برای اطلاعات بیشتر در مورد دنباله ها فصل 16 را ببینید). شما ممکن است متوجه شده باشید که هر جمله در این دنباله به اندازۀ یکی بیشتر از تفاضل بین آن عدد و عدد قبلی اش می باشد. چی شد؟ اوکی، اجازه دهید آن را به روش دیگری توضیح دهم: برای یافتن هر جمله، به جملۀ قبلی آن \(2\) را اضافه می کنید، سپس \(3\) را اضافه می کنید، سپس \(4\) ، سپس \(5\) ، و به همین ترتیب ادامه می دهید.
فرمول یافتن \(n\)امین عدد مثلثی برابر است با \(\frac{n^2+n}{2}\) . در اینجا چگونگی استفاده از این فرمول برای یافتن هشتمین عدد مثلثی را می بینید (یک عدد بعد از عدد \(28\) که در لیست پیشین دیدید):
$$ \frac{8^2+8}{2}=\frac{64+8}{2}=\frac{72}{2}=36 $$
عدد \(36\) تعداد \(8\) واحد بزرگتر از عدد \(28\) می باشد، که خود آن هم \(7\) واحد بزرگتر از \(21\) است، و به همین ترتیب. شما همچنین می توانید اعداد مثلثی را با شمارش نقطه های متصل در یک آرایش مثلثی شکل، نشان دهید:

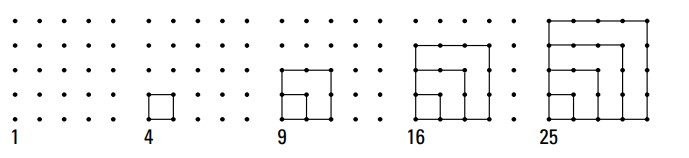
مربع (squares) اعداد باید برای شما آشنا باشد: \(1, 4, 9, 16, 25, 36, ...\) . همانطور که در شکل بعدی می بینید، نقطه های متصل در آرایش می تواند اعداد مربع را نشان بدهد. مربع های کامل در جبر و هندسه همواره نشان داده می شوند. هنگام کار با معادلات درجه دوم و مخروطی ها، مربع ها را می بینید. در هندسه، قضیۀ معروف فیثاغورث به مربع ها وابسته است (مجموع مربع دو ضلع کوچکتر یک مثلث قائم الزاویه برابر است با مربع ضلع بزرگترِ آن).
اعداد شش ضلعی (Hexagonal numbers) در دنبالۀ \(1, 7, 19, 37, 61, 91, ...\) ظاهر می شوند. شما می توانید این اعداد را با ترسیم شش ضلعی ها، و سپس ترسیم شش ضلعی ها در اطراف شش ضلعی ها، نشان دهید، و به همین ترتیب؛ سپس مشابه آنچه در تصویر زیر می بینید، شمارش می کنید که چندتا شش ضلعی دارید:
اگر به ترسیم شش ضلعی ها علاقه مند نباشید، روش دیگری که با استفاده از آن می توانید اعداد شش ضلعی را لیست کنید، فرمول یافتن \(n\)امین عدد شش ضلعی می باشد: \(n^3-(n-1)^3\) یا \(3n^2-3n+1\) . شما ممکن استاز روی این الگو متوجه شده باشید که عدد شش ضلعی بعدی را با اضافه کردن شش به تفاضل بین آن عدد با عدد قبلی اش، ایجاد می کنید. از آنجا که، این اعداد خیلی سریع، بسیار بزرگ می شوند، بنابراین این فرمول می تواند خیلی کمک کند. به عنوان مثال، برای یافتن دهمین عدد دنباله با استفاده از این فرمول خواهید داشت:
$$ 10^3-(10-1)^3=10^3-9^3=1,000-729=271 $$
یک عدد کامل (perfect number) عددی است که برابر با مجموع مقسوم علیه های واقعی (proper divisors) خودش باشد. به عنوان مثال، عدد \(6\) یک عدد کامل می باشد، زیرا \(1+2+3=6\) . چند عدد کامل بعدی عبارتند از \(28 (1 + 2 + 4 + 7 + 14)\) ، \(496 (1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248)\) ، و \(8,128\) . توجه داشته باشید که چگونه تمامی این اعداد کامل (به جز \(1\)) با یکدیگر جفت هستند. این جفتها در یکدیگر ضرب می شوند تا عدد موجود در سوال را به شما بدهند: در مورد \(28\)، داریم \(2\) ضربدر \(14\) ، \(4\) ضربدر \(7\). آیا می توانید تمامی مقسوم علیه های واقعی عدد \(8,128\) را بیابید؟ خوش بگذرانید! هیچ فرمول جادویی برای یافتن این اعداد وجود ندارد. صرفاً ماشین حسابتان را بیرون آورید!
دو عدد متحابه (amicable) هستند، اگر هر کدام از این اعداد برابر با مجموع مقسوم علیه های واقعی عدد دیگر باشد. به عنوان مثال، اعداد \(284\) و \(220\) متحابه می باشند، زیرا مجموع مقسوم علیه های واقعی \(284\) برابر با \(220 (1 + 2 + 4 + 71 + 142)\) می باشد، و مجموع مقسوم علیه های واقعیِ \(220\) برابر با \(284 (1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 +110)\) می باشد. سایر مجموعه های اعداد متحابه عبارت از \(1,184-1,210\) و \(17,296-18,416\) می باشند. آیا به دنبال اعداد متحابه بیشتری هستید؟ به دنبالش بروید، اما انتظار یک فرمول جادویی را نداشته باشید که به شما کمک کند.
عددی خوشحال (happy) در نظر گرفته می شود که مجموع مربع ارقام آن، یا مجموع مربعِ مجموع مربع های آن، برابر با یک باشد.
به عنوان مثال، عدد \(203\) یک عدد خوشحال می باشد، زیرا مجموع مربع های ارقام آن برابر است با \(2^2 + 0^2 + 3^2 = 4 + 9 = 13\) ؛ مجموع مربع های ارقام \(13\) برابر است با \(1^2 + 3^2 = 1 + 9 = 10\) ؛ و مجموع مربع های \(10\) برابر است با \(1^2 + 0^2 = 1\) . شما ممکن است از این موضوع سورپرایز شوید که عدد خوشحال بزرگتری همچون \(2,211\) مراحل کمتری دارد! \(2^2 + 2^2 + 1^2 + 1^2 = 4 + 4 + 1 + 1 = 10\) ، و \(1^2 + 0^2 = 1\) .
یک عدد زائد (abundant number) عددی می باشد که دارای یک قاعده است: مجموع مقسوم علیه های آن باید بزرگتر از دوبرابر عدد باشند. به عنوان مثال، عدد \(12\) زائد می باشد، زیرا \(1 + 2 + 3 + 4 + 6 + 12 = 28\) و \(28\) بزرگتر از دوبرابر \(12\) می باشد. برخی از اعداد زائد دیگر عبارت از \( 18, 20, 24, 30, 36, 100\) می باشند.
یک عدد ناقص (deficient number) قانونی تقریباً مشابه قانون یک عدد زائد دارد. اگر مجموع مقسوم علیه های واقعیِ یک عدد کوچکتر از عدد اصلی باشد، آن عدد، عددی ناقص می باشد. یک مثال از اعداد ناقص \(15\) است، زیرا مجموع مقسوم علیه های واقعیِ آن \(1 + 3 + 5 = 9\)، و \(9\) کوچکتر از \(15\) است. در مورد عدد \(32\) چطور؟ آیا عددی ناقص است؟ مجموع مقسوم علیه های واقعی آن برابر است با \(1 + 2 + 4 + 8 + 16 = 31\) ، بنابراین \(32\) نیز یک عدد ناقص است.
یک عدد خودشیفته (narcissistic number) عددی است که شما می توانید آن را با استفاده از عملیاتی که شامل تمامی ارقام آن عدد می گردد، بنویسید. به عنوان مثال، عدد \(371\) یک عدد خودشیفته می باشد، زیرا اگر ارقام آن ـــ \(3\) ، \(7\) ، و \(1\) ـــ را بگیرید و هر کدام را به توان سوم برسانید، و این توانها را با یکدیگر جمع بزنید، به عدد اصلی می رسید: \(3^3 + 7^3 + 1^3 = 27 + 343 + 1= 371\) . عدد خودشیفتۀ دیگر \(2,427\) می باشد، زیرا شما می توانید ارقام آن را به توانهایی متوالی برسانید، و توانها را با یکدیگر جمع بزنید، و به عدد اصلی برسید: \(2^1 + 4^2 + 2^3 + 7^4 = 2 + 16 + 8 + 2,401 = 2,427\) . احتمالات ممکن برای اعداد خودشیفته بی نهایت می باشند.
یک عدد اول (prime number) فقط بر عدد \(1\) و خودش بخش پذیر می باشد. \(15\) عدد اول آغازین عبارتند از: \(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47\) . با وجود اینکه ریاضیدانان برای قرنها بر روی اعداد اول کار کرده اند، اما هنوز نتوانسته اند فرمول یا الگویی پیدا کنند که تمامی اعداد اول را پیش بینی کند.
یک حدس (conjecture) مشهور، شامل حدس گلدباخ (Goldbach’s Conjecture) می باشد. گلدباخ استدلال نظری کرده است که شما می توانید هر عدد بزرگتر از دو را به صورت مجموع دو عدد اول بنویسید. به عنوان مثال، \(8 = 3 + 5, 20 = 7 + 13\) و به همین ترتیب.
افرادیکه به کامپیوترهای قوی و زمانهای زیاد برای محاسبه مجهز هستند، همواره اعداد اول جدیدی را شناسایی می کنند، اما این اتفاق به وفور رخ نمی دهد. اگر به دنبال این هستید که با یافتن اعداد اول، کسب درآمد کنید عبارت Mersenne Primes را در اینترنت جستجو کنید. به کسانی که بتوانند این اعداد اول را بیابند جوایزی تا سقف \($150,000\) تعلق می گیرد.

اعداد مثلثی
اعداد مثلثی (Triangular numbers) اعدادی هستند که در دنبالۀ \(1, 3, 6, 10, 15, 21, 28, ...\) قرار دارند (برای اطلاعات بیشتر در مورد دنباله ها فصل 16 را ببینید). شما ممکن است متوجه شده باشید که هر جمله در این دنباله به اندازۀ یکی بیشتر از تفاضل بین آن عدد و عدد قبلی اش می باشد. چی شد؟ اوکی، اجازه دهید آن را به روش دیگری توضیح دهم: برای یافتن هر جمله، به جملۀ قبلی آن \(2\) را اضافه می کنید، سپس \(3\) را اضافه می کنید، سپس \(4\) ، سپس \(5\) ، و به همین ترتیب ادامه می دهید.
فرمول یافتن \(n\)امین عدد مثلثی برابر است با \(\frac{n^2+n}{2}\) . در اینجا چگونگی استفاده از این فرمول برای یافتن هشتمین عدد مثلثی را می بینید (یک عدد بعد از عدد \(28\) که در لیست پیشین دیدید):
$$ \frac{8^2+8}{2}=\frac{64+8}{2}=\frac{72}{2}=36 $$
عدد \(36\) تعداد \(8\) واحد بزرگتر از عدد \(28\) می باشد، که خود آن هم \(7\) واحد بزرگتر از \(21\) است، و به همین ترتیب. شما همچنین می توانید اعداد مثلثی را با شمارش نقطه های متصل در یک آرایش مثلثی شکل، نشان دهید:

اعداد مربع
مربع (squares) اعداد باید برای شما آشنا باشد: \(1, 4, 9, 16, 25, 36, ...\) . همانطور که در شکل بعدی می بینید، نقطه های متصل در آرایش می تواند اعداد مربع را نشان بدهد. مربع های کامل در جبر و هندسه همواره نشان داده می شوند. هنگام کار با معادلات درجه دوم و مخروطی ها، مربع ها را می بینید. در هندسه، قضیۀ معروف فیثاغورث به مربع ها وابسته است (مجموع مربع دو ضلع کوچکتر یک مثلث قائم الزاویه برابر است با مربع ضلع بزرگترِ آن).

اعداد شش ضلعی
اعداد شش ضلعی (Hexagonal numbers) در دنبالۀ \(1, 7, 19, 37, 61, 91, ...\) ظاهر می شوند. شما می توانید این اعداد را با ترسیم شش ضلعی ها، و سپس ترسیم شش ضلعی ها در اطراف شش ضلعی ها، نشان دهید، و به همین ترتیب؛ سپس مشابه آنچه در تصویر زیر می بینید، شمارش می کنید که چندتا شش ضلعی دارید:
اگر به ترسیم شش ضلعی ها علاقه مند نباشید، روش دیگری که با استفاده از آن می توانید اعداد شش ضلعی را لیست کنید، فرمول یافتن \(n\)امین عدد شش ضلعی می باشد: \(n^3-(n-1)^3\) یا \(3n^2-3n+1\) . شما ممکن استاز روی این الگو متوجه شده باشید که عدد شش ضلعی بعدی را با اضافه کردن شش به تفاضل بین آن عدد با عدد قبلی اش، ایجاد می کنید. از آنجا که، این اعداد خیلی سریع، بسیار بزرگ می شوند، بنابراین این فرمول می تواند خیلی کمک کند. به عنوان مثال، برای یافتن دهمین عدد دنباله با استفاده از این فرمول خواهید داشت:
$$ 10^3-(10-1)^3=10^3-9^3=1,000-729=271 $$
اعداد کامل
یک عدد کامل (perfect number) عددی است که برابر با مجموع مقسوم علیه های واقعی (proper divisors) خودش باشد. به عنوان مثال، عدد \(6\) یک عدد کامل می باشد، زیرا \(1+2+3=6\) . چند عدد کامل بعدی عبارتند از \(28 (1 + 2 + 4 + 7 + 14)\) ، \(496 (1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248)\) ، و \(8,128\) . توجه داشته باشید که چگونه تمامی این اعداد کامل (به جز \(1\)) با یکدیگر جفت هستند. این جفتها در یکدیگر ضرب می شوند تا عدد موجود در سوال را به شما بدهند: در مورد \(28\)، داریم \(2\) ضربدر \(14\) ، \(4\) ضربدر \(7\). آیا می توانید تمامی مقسوم علیه های واقعی عدد \(8,128\) را بیابید؟ خوش بگذرانید! هیچ فرمول جادویی برای یافتن این اعداد وجود ندارد. صرفاً ماشین حسابتان را بیرون آورید!
اعداد متحابه
دو عدد متحابه (amicable) هستند، اگر هر کدام از این اعداد برابر با مجموع مقسوم علیه های واقعی عدد دیگر باشد. به عنوان مثال، اعداد \(284\) و \(220\) متحابه می باشند، زیرا مجموع مقسوم علیه های واقعی \(284\) برابر با \(220 (1 + 2 + 4 + 71 + 142)\) می باشد، و مجموع مقسوم علیه های واقعیِ \(220\) برابر با \(284 (1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 +110)\) می باشد. سایر مجموعه های اعداد متحابه عبارت از \(1,184-1,210\) و \(17,296-18,416\) می باشند. آیا به دنبال اعداد متحابه بیشتری هستید؟ به دنبالش بروید، اما انتظار یک فرمول جادویی را نداشته باشید که به شما کمک کند.
اعداد خوشحال
عددی خوشحال (happy) در نظر گرفته می شود که مجموع مربع ارقام آن، یا مجموع مربعِ مجموع مربع های آن، برابر با یک باشد.
به عنوان مثال، عدد \(203\) یک عدد خوشحال می باشد، زیرا مجموع مربع های ارقام آن برابر است با \(2^2 + 0^2 + 3^2 = 4 + 9 = 13\) ؛ مجموع مربع های ارقام \(13\) برابر است با \(1^2 + 3^2 = 1 + 9 = 10\) ؛ و مجموع مربع های \(10\) برابر است با \(1^2 + 0^2 = 1\) . شما ممکن است از این موضوع سورپرایز شوید که عدد خوشحال بزرگتری همچون \(2,211\) مراحل کمتری دارد! \(2^2 + 2^2 + 1^2 + 1^2 = 4 + 4 + 1 + 1 = 10\) ، و \(1^2 + 0^2 = 1\) .
اعداد زائد
یک عدد زائد (abundant number) عددی می باشد که دارای یک قاعده است: مجموع مقسوم علیه های آن باید بزرگتر از دوبرابر عدد باشند. به عنوان مثال، عدد \(12\) زائد می باشد، زیرا \(1 + 2 + 3 + 4 + 6 + 12 = 28\) و \(28\) بزرگتر از دوبرابر \(12\) می باشد. برخی از اعداد زائد دیگر عبارت از \( 18, 20, 24, 30, 36, 100\) می باشند.
اعداد ناقص
یک عدد ناقص (deficient number) قانونی تقریباً مشابه قانون یک عدد زائد دارد. اگر مجموع مقسوم علیه های واقعیِ یک عدد کوچکتر از عدد اصلی باشد، آن عدد، عددی ناقص می باشد. یک مثال از اعداد ناقص \(15\) است، زیرا مجموع مقسوم علیه های واقعیِ آن \(1 + 3 + 5 = 9\)، و \(9\) کوچکتر از \(15\) است. در مورد عدد \(32\) چطور؟ آیا عددی ناقص است؟ مجموع مقسوم علیه های واقعی آن برابر است با \(1 + 2 + 4 + 8 + 16 = 31\) ، بنابراین \(32\) نیز یک عدد ناقص است.
اعداد خود شیفته
یک عدد خودشیفته (narcissistic number) عددی است که شما می توانید آن را با استفاده از عملیاتی که شامل تمامی ارقام آن عدد می گردد، بنویسید. به عنوان مثال، عدد \(371\) یک عدد خودشیفته می باشد، زیرا اگر ارقام آن ـــ \(3\) ، \(7\) ، و \(1\) ـــ را بگیرید و هر کدام را به توان سوم برسانید، و این توانها را با یکدیگر جمع بزنید، به عدد اصلی می رسید: \(3^3 + 7^3 + 1^3 = 27 + 343 + 1= 371\) . عدد خودشیفتۀ دیگر \(2,427\) می باشد، زیرا شما می توانید ارقام آن را به توانهایی متوالی برسانید، و توانها را با یکدیگر جمع بزنید، و به عدد اصلی برسید: \(2^1 + 4^2 + 2^3 + 7^4 = 2 + 16 + 8 + 2,401 = 2,427\) . احتمالات ممکن برای اعداد خودشیفته بی نهایت می باشند.
اعداد اول
یک عدد اول (prime number) فقط بر عدد \(1\) و خودش بخش پذیر می باشد. \(15\) عدد اول آغازین عبارتند از: \(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47\) . با وجود اینکه ریاضیدانان برای قرنها بر روی اعداد اول کار کرده اند، اما هنوز نتوانسته اند فرمول یا الگویی پیدا کنند که تمامی اعداد اول را پیش بینی کند.
یک حدس (conjecture) مشهور، شامل حدس گلدباخ (Goldbach’s Conjecture) می باشد. گلدباخ استدلال نظری کرده است که شما می توانید هر عدد بزرگتر از دو را به صورت مجموع دو عدد اول بنویسید. به عنوان مثال، \(8 = 3 + 5, 20 = 7 + 13\) و به همین ترتیب.
افرادیکه به کامپیوترهای قوی و زمانهای زیاد برای محاسبه مجهز هستند، همواره اعداد اول جدیدی را شناسایی می کنند، اما این اتفاق به وفور رخ نمی دهد. اگر به دنبال این هستید که با یافتن اعداد اول، کسب درآمد کنید عبارت Mersenne Primes را در اینترنت جستجو کنید. به کسانی که بتوانند این اعداد اول را بیابند جوایزی تا سقف \($150,000\) تعلق می گیرد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: