خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
نقاط هم راستا، نقاط هم صفحه

چیز زیادی در مورد نقاط نمی توان گفت. آنها هیچ ویژگی ندارند، و هر کدام از آنها دقیقاً مشابه دیگری می باشد. هرچند، گروه های متنوعی از نقاط، شایستگی یک توصیف را دارند:

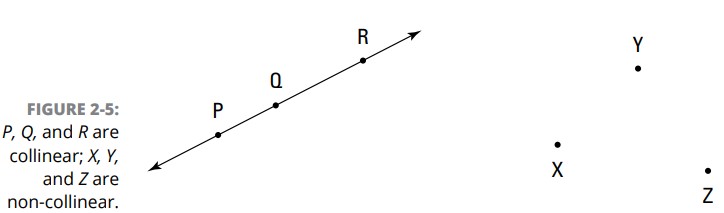
نقاط هم راستا نقاطی هستند که روی یک خط راست قرار گرفته اند. هر دو نقطه ای با یکدیگر هم راستا هستند، زیرا شما می توانید همیشه با یک خط راست آنها را به هم متصل کنید. سه یا چند نقطه می توانند هم راستا باشند، اما الزامی هم نیست که هم راستا باشند. شکل 5-2 را ببینید.
نقاطی همچون نقاط \(X\) ، \(Y\) ، و \(Z\) در شکل 5-2 که همگی آنها بر روی یک خط راست قرار نگرفته اند، نقاط غیر هم راستا نامیده می شوند.
یک گروه از نقاط که در صفحۀ یکسانی قرار گرفته باشند، نقاط هم صفحه نامیده می شوند. هر دو یا سه نقطه، همواره هم صفحه هستند. چهار یا تعداد بیشتری نقطه، ممکن است هم صفحه باشند و یا اینکه نباشند.
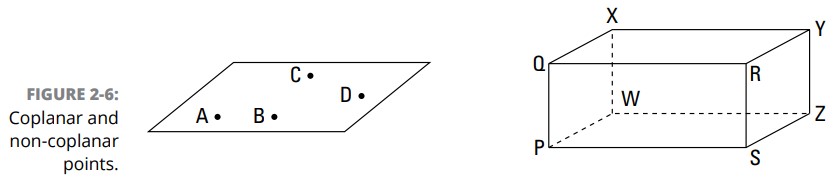
به شکل 6-2 نگاه کنید، که نقاط هم صفحۀ \(A\) ، \(B\) ، \(C\) ، و \(D\) را به شما نشان می دهد. در جعبۀ سمت راست مجموعه های زیادی از نقاط هم صفحه وجود دارند. به عنوان مثال، نقاط \(P\)، \(Q\)، \(X\)، و \(W\) هم صفحه هستند؛ صفحه موجود در سمت چپ مکعب، شامل این نقاط می باشد. توجه داشته باشید که نقاط \(Q\)، \(X\)، \(S\)، و \(Z\) نیز هم صفحه هستند، هرچند صفحه ای که شامل آنها می باشد، نشان داده نشده است؛ این صفحه جعبه را به صورت مورب قطع می کند.
یک گروه از نقاط که همگی در یک صفحه قرار نگرفته اند را نقاط غیر هم صفحه می نامند.
شکل 6-2 را ببینید. نقاط \(P\)، \(Q\)، \(X\)، و \(Y\) غیر هم صفحه هستند. بالای مکعب شامل نقاط \(Q\)، \(X\)، و \(Y\) می باشد و سمت چپ شامل نقاط \(P\)، \(Q\)، و \(X\) هستند، اما هیچ سطح صافی شامل هر چهار تایِ این نقاط نمی گردد.

نقاط هم راستا (Collinear points)
نقاط هم راستا نقاطی هستند که روی یک خط راست قرار گرفته اند. هر دو نقطه ای با یکدیگر هم راستا هستند، زیرا شما می توانید همیشه با یک خط راست آنها را به هم متصل کنید. سه یا چند نقطه می توانند هم راستا باشند، اما الزامی هم نیست که هم راستا باشند. شکل 5-2 را ببینید.
نقاط غیر هم راستا (Non-collinear points)
نقاطی همچون نقاط \(X\) ، \(Y\) ، و \(Z\) در شکل 5-2 که همگی آنها بر روی یک خط راست قرار نگرفته اند، نقاط غیر هم راستا نامیده می شوند.

نقاط هم صفحه (Coplanar points)
یک گروه از نقاط که در صفحۀ یکسانی قرار گرفته باشند، نقاط هم صفحه نامیده می شوند. هر دو یا سه نقطه، همواره هم صفحه هستند. چهار یا تعداد بیشتری نقطه، ممکن است هم صفحه باشند و یا اینکه نباشند.
به شکل 6-2 نگاه کنید، که نقاط هم صفحۀ \(A\) ، \(B\) ، \(C\) ، و \(D\) را به شما نشان می دهد. در جعبۀ سمت راست مجموعه های زیادی از نقاط هم صفحه وجود دارند. به عنوان مثال، نقاط \(P\)، \(Q\)، \(X\)، و \(W\) هم صفحه هستند؛ صفحه موجود در سمت چپ مکعب، شامل این نقاط می باشد. توجه داشته باشید که نقاط \(Q\)، \(X\)، \(S\)، و \(Z\) نیز هم صفحه هستند، هرچند صفحه ای که شامل آنها می باشد، نشان داده نشده است؛ این صفحه جعبه را به صورت مورب قطع می کند.
نقاط غیر هم صفحه (Non-coplanar points)
یک گروه از نقاط که همگی در یک صفحه قرار نگرفته اند را نقاط غیر هم صفحه می نامند.
شکل 6-2 را ببینید. نقاط \(P\)، \(Q\)، \(X\)، و \(Y\) غیر هم صفحه هستند. بالای مکعب شامل نقاط \(Q\)، \(X\)، و \(Y\) می باشد و سمت چپ شامل نقاط \(P\)، \(Q\)، و \(X\) هستند، اما هیچ سطح صافی شامل هر چهار تایِ این نقاط نمی گردد.

لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: