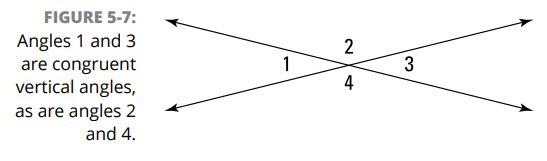
هنگامی که دو خط یکدیگر را قطع می کنند و یک X می سازند، زوایه های روبروی یکدیگر در این X زوایای متقابل به رأس (vertical angles) نامیده می شوند (در فصل 2 این زوایا را معرفی کردیم). این زاویه ها برابر هستند، و در اینجا قضیۀ رسمی که این موضوع را به شما می گوید، داریم.








در اینجا یک مسألۀ جبری هندسی داریم که این مفهوم ساده را توصیف می کند: اندازۀ این شش زاویۀ موجود در شکل زیر را تعیین کنید.


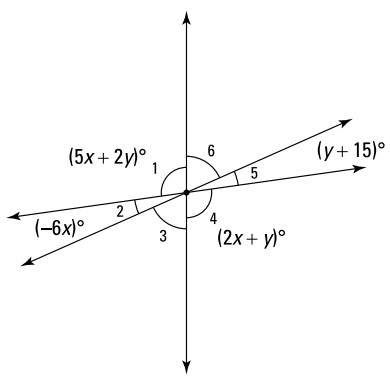
زاویه های متقابل به رأس با یکدیگر همنهشت هستند، بنابراین \(\angle{1} \cong \angle{4}\) و \(\angle{2} \cong \angle{5}\) ؛ و از این رو شما می توانید اندازه های آنها را برابر با یکدیگر قرار دهید:
$$
\begin{array}{c c c}
\angle{1} \cong \angle{4} & \text{ and } & \angle{2} \cong \angle{5} \\[2ex]
5x+2y=2x+y & & -6x=y+15
\end{array}
$$
اکنون دستگاهی متشکل از دو معادله و دو مجهول دارید. برای حل کردن این دستگاه، ابتدا هر معادله را برای بدست آوردن \(y\) حل کنید:
$$
\begin{array}{c c c}
y=-3x & & y=-6x-15
\end{array}
$$
سپس، از آنجا که هر دوی این معادلات برای \(y\) حل شده اند، شما می توانید دو عبارت \(x\) را برابر با یکدیگر قرار بدهید و آن را برای \(x\) حل کنید:
$$
-3x=-6x-15 \\[2ex]
3x=-15 \\[2ex]
x=-5
$$
برای بدست آوردن \(y\)، عدد \(-5\) را برای \(x\) در معادلۀ ساده شدۀ اول جایگذاری کنید:
$$
y=-3x \\[2ex]
y=-3(-5) \\[2ex]
y=15
$$
اکنون \(-5\) و \(15\) را در عبارات زاویه ها جایگذاری کنید تا مقادیر چهار تا از این شش زاویه را بدست آورید:
$$
\angle{4} \cong \angle{1}=5x+2y=5(-5)+2(15)=5^{\circ} \\[2ex]
\angle{5} \cong \angle{2} = -6x=-6(-5)=30^{\circ}
$$
برای بدست آوردن \(\angle{3}\) ، توجه داشته باشید که \(\angle{1}\) ، \(\angle{2}\) ، و \(\angle{3}\) یک زاویۀ نیم صفحه را تشکیل می دهند، بنابراین مجموع آنها \(180^{\circ}\) می باشد:
$$
\angle{1} + \angle{2}+\angle{3}=180^{\circ} \\[2ex]
5^{\circ}+30^{\circ}+\angle{3}=180^{\circ}\\[2ex]
\angle{3}=145^{\circ}
$$
در پایان، \(\angle{3}\) و \(\angle{6}\) زاویه های متقابل به رأس همنهشت می باشند، بنابراین \(\angle{6}\) نیز باید برابر با \(145^{\circ}\) باشد. آیا متوجه شدید که زاویه های موجود در شکل خارج از مقیاس می باشند؟ فراموش نکنید که شما نمی توانید چیزی را در مورد اندازه های مرتبط زاویه ها یا پاره خطها از روی شکل هندسی فرض بگیرید (فصل 3 را ببینید).