خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
اثبات های طولانی تر در هندسه

فصل های 4 و 5 شما را با اثبات های کوتاه و چندین قضیۀ ساده در هندسه آشنا کردند. در اینجا، یک اثبات طولانی تر و مشکل تر را با جزئیات کامل آن بررسی خواهید کرد، هر مرحله از این اثبات به دقت تجزیه و تحلیل گردیده است. در طول این فصل، من شما را به صورت گام به گام با فرآیند کلی تفکر، که وارد فعالیت های حل کردن یک اثبات، مرور و توسعۀ استراتژی های فصل های 4 و 5 می گردد، پیش می برم. هنگامی که شما بر روی یک اثبات کار می کنید و جایی از آن گیر می کنید، این فصل محل خوبی است که به آن مراجعۀ دوباره ای داشته باشید و نکاتی را برای از سرگیری دوبارۀ حرکت بیاموزید.

اثباتی که برای این فصل ایجاد کرده ام، خیلی مشکل نیست؛ فقط از اثبات هایی که در فصل 5 دیدید، طولانی تر می باشد.
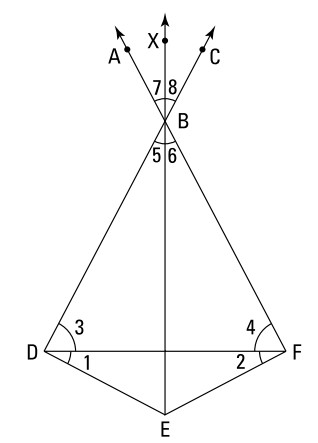
داده ها:
\(\overline{BD} \bot \overline{DE}\)
\(\overline{BF} \bot \overline{EF}\)
\(\angle{1} \cong \angle{2}\)
\(\angle{5}\) متمم \(\angle{3}\) می باشد
\(\angle{6}\) متمم \(\angle{4}\) می باشد
اثبات کنید:
\(\overrightarrow{BX}\) ، \(\angle{ABC}\) را تنصیف می کند
یک روش خوب برای آغاز هر اثباتی اینست که یک استراتژی بازی (game plan)، یا طرح کلی حدسی، از چگونگی انجام اثبات بسازید. روش رسمی نوشتن یک اثبات دو ستونی، مخصوصاً در ابتدا می تواند مشکل باشد ـــ تقریباً شبیه یادگیری یک زبان خارجی می باشد. اگر یک اثبات را به دو یا چند بخش کوتاه تر و قابلیت مدیریت تر بشکنید، نوشتن آن ساده تر می شود.
در ابتدا، شما یک استراتژی بازی را می نویسید یا به سادگی آن را در نظر می گیرید، که در آن شما با عقل و درایت خودتان، و بدون اینکه با نگارش صحیح زبان فنی درگیر گردید، وارد منطق اثبات می شوید. هنگامی که این کار را انجام دادید، گام دوم یعنی ترجمۀ این منطق به شکل دو ستونی زیاد سخت نخواهد بود.
در اینجا یک استراتژی بازیِ ممکن برای اثباتی که مشغول کار با آن هستیم را می بینید: داده های این اثبات برای شما دو جفت از پاره خطهای متعامد را تدارک دیده اند؛ که به شما \(90^{\circ}\) برای \(\angle{BDE}\) و \(\angle{BFE}\) را می دهد. سپس، فرض کنید زوایای همنهشت \(\angle{1}\) و \(\angle{2}\) هر دو برابر با \(30^{\circ}\) باشند. این منجر می شود تا \(\angle{3}\) و \(\angle{4}\) هر دو برابر با \(90^{\circ} - 30^{\circ}\) یا \(60^{\circ}\) گردند. سپس، از آنجا که \(\angle{3}\) و \(\angle{5}\)، همچنین \(\angle{4}\) و \(\angle{6}\) متمم هستند، \(\angle{5}\) و \(\angle{6}\) هر دو باید \(30^{\circ}\) باشند. زاویه های \(5\) و \(8\) و همچنین \(\angle{6}\) و \(\angle{7}\)، زوایای متقابل به رأس می باشند، بنابراین \(\angle{7}\) و \(\angle{8}\) نیز باید \(30^{\circ}\) باشند ـــ و از این رو آنها همنهشت می باشند. در آخر، از آنجا که \(\angle{7} \cong \angle{8}\) ، در نتیجه \(\angle{ABC}\) تنصیف شده است. تمام شد.
هنگام انجام یک اثبات، با دقت در نظر گرفتن نتایج طرح اولیۀ استدلالهای اثبات، همانند استراتژی بازی پیشین، همیشه ایدۀ خوبی است. اگرچه، احتمالاً مواقعی باشد که شما نتوانید کل استدلال را فوراً متوجه شوید. اگر این اتفاق برای شما بیفتد، شما می توانید از استراتژی هایی که در بقیۀ این فصل ارائه شده اند تا به جنبه های مختلف اثبات فکر کنید. همچنین بخشهایی که به زودی خواهید دید، برخی نکات را برای شما فراهم آورده اند، که می توانند به شما کمک کنند اسکلت اصلیِ استراتژی بازی را به شکل یک اثبات دو ستونی تصحیح کنید.
شاید شما استراتژی بازی موجود در بخش قبل را دنبال نکنید ـــ یا شما آن را درک کرده اید اما فکر نمی کنید که خودتان قادر باشید به آن نتایج در نگاه اول برسید ـــ بنابراین شما به اثبات خیره شده اید و نمی دانید از کجا باید آغاز کنید. توصیۀ من: تمامی داده های اثبات را بررسی کنید و از خودتان بپرسید، چرا آنها هر داده ای را به شما داده اند.
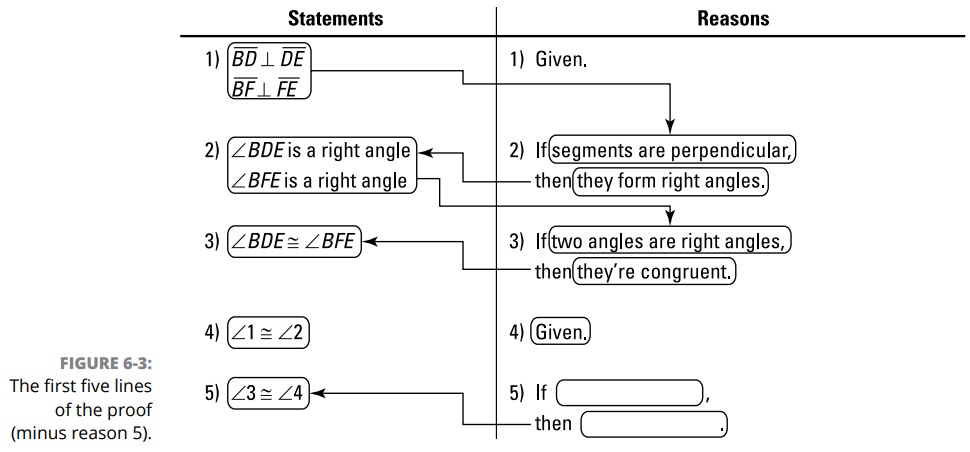
به پنج دادۀ این اثبات نگاه کنید. فوراً آشکار نمی شود که سومین، چهارمین، و پنجمین داده چگونه می توانند به شما کمک کنند، اما در مورد دو دادۀ اول، یعنی پاره خطهای متعامد، چطور؟ چرا آنها باید این داده ها را به شما بدهند؟ خطهای متعامد چه چیزی را به شما می دهند؟ قطعاً، زوایه های قائمه. اوکی، بنابراین شما مسیر حرکت خودتان را پیدا کرده اید ـــ اکنون دو خط اول از اثبات را می دانید (شکل 1-6 را ببینید).

توجه داشته باشید که اگر بدانید چگونه ساختار if-then در دلایل کار می کند، دومین دلیل تقریباً خودش را می نویسد (برای اطلاعات بیشتر در مورد منطق if-then بخش بعدی و همینطور فصل 4 را ببینید).
حرکت از داده ها به نتیجه گیریهای نهایی در یک اثبات دو ستونی به نوعی شبیه ضربه زدن به یک ردیف در دومینو می باشد. هر گزاره، مانند هر دومینو، به گزارۀ بعدی ضربه می زند (اگرچه، برخلاف دومینوها، یک گزاره همیشه به یکی بعد از خودش ضربه نمی زند). ساختار جملۀ if-then از هر دلیل در یک اثبات دو ستونی به شما نشان می دهد چگونه هر گزاره به گزارۀ بعدی ضربه می زند. به عنوان مثال، در شکل 1-6 دلیل "اگر دو پاره خط متعامد باشند، سپس آنها یک زاویۀ قائمه را تشکیل می دهند." را در نظر بگیرید، دومینوی متعامد (گزارۀ 1) به دومینوی زاویۀ قائمه ضربه می زند (گزارۀ 2). در شکل 2-6 ، یک خط دیگر به این اثبات اضافه می شود. دلیل 3 به شما توضیح می دهد که چگونه دومینوی زاویۀ قائمه (گزارۀ 2) به دومینویِ زاویه های همنهشت (گزارۀ 3)، ضربه می زند. این فرآیند در سراسر اثبات ادامه می یابد، اما، همانطور که پیشتر اشاره شد، همواره به این سادگی نیست که 1 به دو ضربه بزند، 2 به 3، 3 به 4، و به همین ترتیب. گاهی اوقات شما به دو گزاره نیاز دارید تا به گزارۀ دیگری ضربه بزنند، و گاهی اوقات شما گزاره ها را نادیده می گیرید؛ به عنوان مثال، در اثبات دیگری، گزارۀ 3 ممکن است به گزارۀ 5 ضربه بزند. تمرکز بر روی منطق if-then از یک اثبات، به شما کمک می کند تا ببینید چگونه کل اثبات به یکدیگر متصل می شوند.
یه شکل 1-6 بازگردید و نگاهی به آن بیندازید. از آنجا که تنها گزارۀ موجود در بالای دلیل 2، گزارۀ 1 می باشد، آنجا تنها جایی است که شما می توانید بدنبال مفاهیم موجود در جزء if از دلیل 2 بگردید. بنابراین، اگر شما این اثبات را با قرار دادن دو جفت از پاره خطهای متعامد در گزارۀ 1 آغاز کنید، سپس شما باید از آن اطلاعات در دلیل 2 استفاده نمایید، که باید اینطور آغاز شود "اگر پاره خطها متعامد باشند، سپس ...".
اکنون فرض کنید شما نمی دانید چه چیزی را باید در گزارۀ 2 قرار دهید. ساختار if-then از دلیل 2 به شما کمک می کند آن را بدانید. از آنجا که دلیل 2 اینگونه آغاز می شود "اگر دو پاره خط متعامد باشند ..." شما از خودتان می پرسید، "خوب، اگر دو خط متعامد باشند، چه اتفاقی می افتد؟" پاسخ، قطعاً، اینست که زاویه های قائمه تشکیل می شوند. بنابراین مفهوم زاویۀ قائمه باید در جزء then از دلیل 2 قرار گیرد و در گزارۀ دقیقاً مقابل آن یعنی گزارۀ 2 نیز قرار بگیرد.
اوکی، حالا چی؟ خوب، در مورد دلیل 3 فکر کنید. یک روش می تواند آغاز کردن با زاویه های قائمۀ موجود در گزارۀ 2 باشد. بخش if از دلیل 3 می تواند این باشد "اگر دو زاویه قائمه باشند ..." آیا می توانید این را تمام کنید؟ قطعاً: اگر دو زاویه قائمه باشند، سپس آنها همنهشت می باشند. بنابراین، انجام شد: شما دلیل 3 را یافتید، و گزارۀ 3 باید شامل مفهوم موجود در بخش then از دلیل 3 باشد، همنهشتی زاویه های قائمه. شکل 2-6 این اثبات را تا اینجایِ کار به شما نشان می دهد.

با آن مواجه شوید: شما ممکن است در جایی از اثبات گیر کنید، یا خدای ناکرده، در چندین نقطۀ یک اثبات متوقف شوید! با خودتان بیندیشید وقتی گیر کردید، چه کار باید کنید؟
تا اینجایِ اثبات این فصل، شما دو زاویۀ همنهشت در گزارۀ 3 دارید، اما شما نمی توانید به تنهایی با این مفهوم بیش از این پیش بروید. بنابراین، داده ها را مجدداً بررسی کنید. کدامیک از سه دادۀ استفاده نشده ممکن است گزارۀ 3 را بسازد؟ هیچ روشی وجود ندارد که با اطمینان این سوال را پاسخ دهید، بنابراین شما نیاز دارید تا به غرایزتان اطمینان کنید، داده ای را انتخاب کنید، و آن را امتحان کنید (یا اگر فکر می کنید غریزه ای برای این کار ندارید، سپس فقط چیزی را امتحان کنید، هر چیزی می تواند باشد).
سومین داده به شما میگوید \(\angle{1} \cong \angle{2}\) . این امیدوارکننده به نظر می رسد زیرا زاویه های \(1\) و \(2\) بخشی از زاویه های قائمۀ موجود در گزارۀ 3 می باشند. شما می توانید از خودتان بپرسید، "اگر \(\angle{1}\) و \(\angle{2}\) به عنوان مثال برابر با \(35^{\circ}\) باشند، به دنبال آن چه چیزی خواهد بود؟" شما می دانید که زاویه های قائمه \(90^{\circ}\) می باشند، بنابراین اگر \(\angle{1}\) و \(\angle{2}\) \(35^{\circ}\) باشند، \(\angle{3}\) و \(\angle{4}\) هر دو برابر با \(55^{\circ}\) خواهند بود و بنابراین، قطعاً، آنها همنهشت می باشند. درسته. شما در حال پیشرفت هستید. شما می توانید از آن دادۀ سوم در گزارۀ 4 استفاده کنید و سپس در گزارۀ 5 بیان کنید که \(\angle{3} \cong \angle{4}\) .
شکل 3-6 این اثبات را تا گزارۀ 5 نشان می دهد. حباب ها و فلش ها به شما نشان می دهند چگونه گزاره ها و دلایل به یکدیگر متصل هستند. شما می توانید ببینید که جزء if از هر دلیل به گزاره ای در بالای آن دلیل مرتبط است و جزء then به گزارۀ موجود در همان خط دلیل، مرتبط می باشد. از آنجا که من هنوز از دلیل 5 جلوتر نرفته ام، در شکل موجود نمی باشد. ببینید آیا می توانید قبل از اینکه توضیحاتی را که متعاقباً آمده است بخوانید، دلیل 5 را متوجه گردید. راهنما: بخش then از دلیل 5 باید با گزارۀ 5 که در شکل نشان داده شده است، مرتبط باشد.
خوب، آیا دلیل 5 را متوجه شدید؟ پاسخ آن تفریق زاویه ها می باشد، با استفاده از اندازۀ \(35^{\circ}\) برای \(\angle{1}\) و \(\angle{2}\) ، به اندازۀ \(55^{\circ}\) برای \(\angle{3}\) و \(\angle{4}\) در گزارۀ 5 می رسیم، و شما این پاسخ \(55^{\circ}\) را با انجام یک تفریق، یعنی \(90^{\circ} - 35^{\circ}=55^{\circ}\) بدست می آورید. (این اشتباه را نکنید که فکر کنید این یک جمع زاویه ها می باشد زیرا \(35^{\circ} + 55^{\circ} = 90^{\circ}\) .) شما دو زاویه را از دو زاویۀ دیگر تفریق می کنید، بنابراین از نسخۀ چهار زاویه ای از تفریق زاویه ها استفاده می کنید (فصل 5 را ببینید). بنابراین دلیل 5 می شود "اگر دو زاویۀ همنهشت (\(\angle{1}\) و \(\angle{2}\)) از دو زاویۀ همنهشت دیگر (زاویه های قائمه) تفریق گردند، سپس تفاضل آنها (\(\angle{3}\) و \(\angle{4}\)) همنهشت می باشند."
اگر ندانید این پنج خط شما را به کجا می برند یا اینکه آنها صحیح هستند یا خیر، ممکن است اندکی (یا بیش از اندکی) نگران و مردد شوید. شما ممکن است از خودتان بپرسید "هدف از انجام این کار چیست" ، "اینکه پنج خط را انجام بدهم و در عین حال ندانم که باید به کجا بروم؟". این یک پاسخ و عکس العمل قابل درک است. پاسخش اینست.
احساس نکنید مجبور هستید یک مرتبه به آخر کار برسید و ببنید که کل اثبات چگونه در کنار یکدیگر قرار می گیرد. در عوض، صرفاً به ایجاد یک گام رو به هدف خرسند و راضی باشید (یک گزارۀ بیشتر بدست آورید)، سپس گام بعدی، سپس بعدی، و به همین ترتیب. دیر یا زود به منطقۀ پایانی می رسید. یک بار در مورد دانش آموزی شنیدم که نمراتش در هندسه از C و D به نمرات A و B تغییر یافت، و تمامی این تغییرات فقط بخاطر تغییر تمرکز او از تمرکز بر روی رسیدن به پاسخ نهایی اثبات ها به تمرکز بر روی حرکت قدم به قدم برای حل اثبات بود.
فرض کنید در میانۀ یک اثبات هستید و نمی دانید چگونه باید از جایی که هستید به خط پایانی برسید. نگران نباشید ـــ فقط به آخر اثبات پرش کنید و از آنجا رو به عقب باز گردید.
اوکی، از جایی در اثبات این فصل که متوقف شده ایم دوباره از سر بگیرید: شما پنج خط از این اثبات را تکمیل کرده اید، و به \(\angle{3} \cong \angle{4}\) رسیده اید. حالا کجا باید بروید؟ پیش رفتن از اینجا ممکن است اندکی مهارت آمیز باشد، بنابراین رو به سمت عقب کار کنید. شما می دانید که در آخرین خط از این اثبات باید اثبات شود که: \(\overrightarrow{BX}\) ، \(\angle{ABC}\) را تنصیف می کند. اکنون اگر در مورد اینکه آخرین دلیل چه باید باشد، فکر کنید، یا در مورد اینکه گزارۀ یکی مانده به آخر چه باید باشد، مشکل نخواهد بود که بدانید نیاز به دو زاویۀ همنهشت دارید (دو زاویۀ نصف شده)، تا از روی آن استنتاج کنید که یک زاویۀ بزرگتر تنصیف شده است. شکل 4-6 به شما نشان می دهد آخر اثبات چگونه خواهد بود. به حباب های منطق if-then دقت کنید (جزء if در دلایل به گزارۀ بالای آن دلیل متصل است؛ جزء then در دلایل به گزارۀ موجود در همان خط دلیل متصل است).
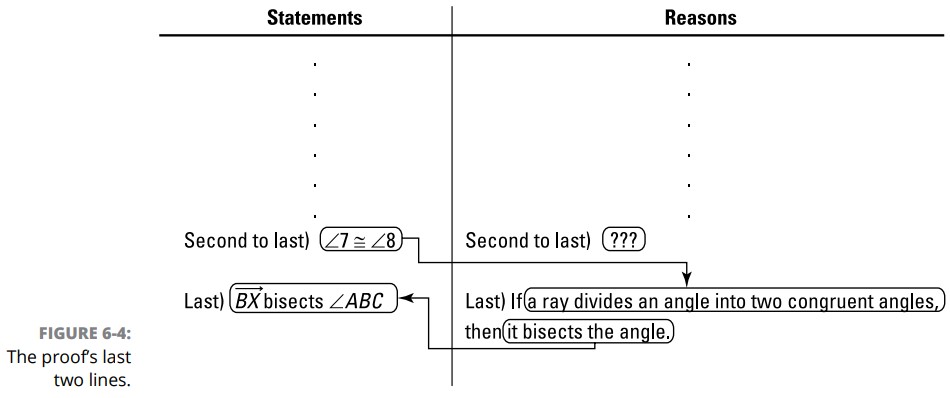
برای ادامه دادن حرکت رو به سمت عقب و رسیدن به گزارۀ دو تا مانده به آخر، سه تا مانده به آخر، و به همین ترتیب، تلاش کنید. (حرکت رو به سمت عقب از میان یک اثبات همواره شامل برخی حدس ها خواهد بود، اما اجازه ندهید این شما را متوقف کند.) چرا ممکن است \(\angle{7}\) با \(\angle{8}\) همنهشت باشد؟ خوب، احتمالاً نیازی ندارید خیلی سخت بررسی کنید تا جفتی از زوایای متقابل به رأس همنهشت را بیابید، \(\angle{5}\) و \(\angle{8}\) ، و جفتی دیگر، \(\angle{6}\) و \(\angle{7}\).
اوکی، شما نیاز دارید تا نشان دهید که \(\angle{7}\) با \(\angle{8}\) همنهشت می باشد، و شما می دانید که \(\angle{6}\) با \(\angle{7}\) برابر می باشد، و \(\angle{5}\) با \(\angle{8}\) برابر می باشد. بنابراین اگر شما بدانید که زوایای \(\angle{5}\) و \(\angle{6}\) همنهشت می باشند، موفقیتتان قطعی خواهد بود.
حالا که چند مرحله رو به سمت عقب حرکت کردید، در اینجا استدلالی رو به سمت جلو داریم: این اثبات می تواند در گزارۀ سه تا مانده به آخر بیان کند \(\angle{5} \cong \angle{6}\) ، سپس در دو تا مانده به آخرین گزاره بیان دارد که \(\angle{5} \cong \angle{8}\) و \(\angle{6} \cong \angle{7}\) (زیرا زوایای متقابل به رأس با یکدیگر همنهشت می باشند)، و سپس در گزارۀ یکی مانده به آخر بیان کند که \(\angle{7} \cong \angle{8}\) (با استفاده از ویژگی تراگذری برای چهار زاویه. فصل 5 را ببینید). شکل 5-6 نشان می دهد تمامی اینها در شکل دو ستونی چگونه نوشته می شوند.
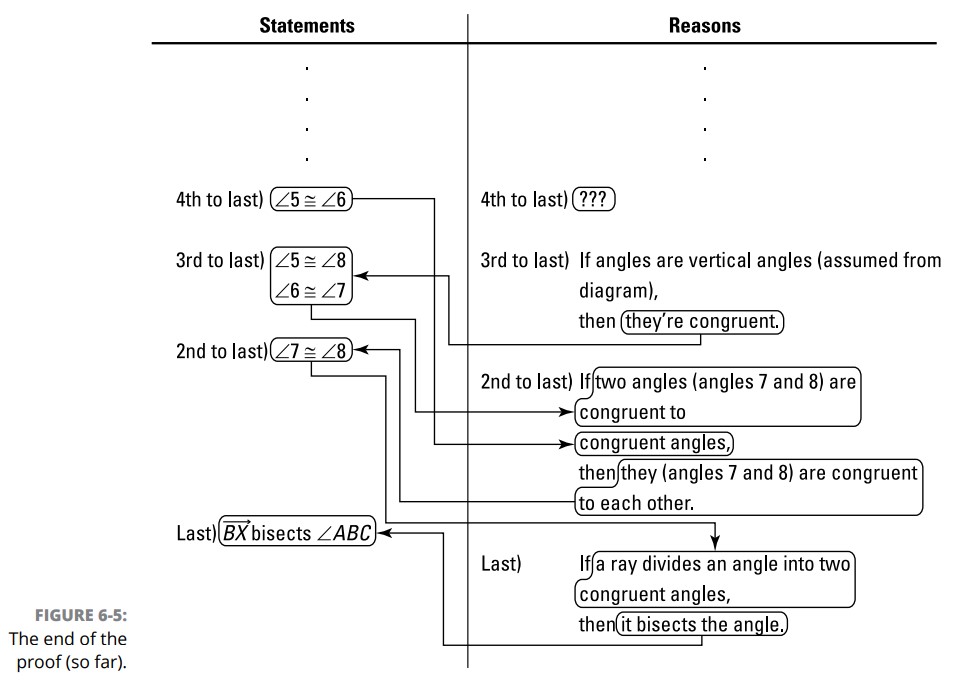
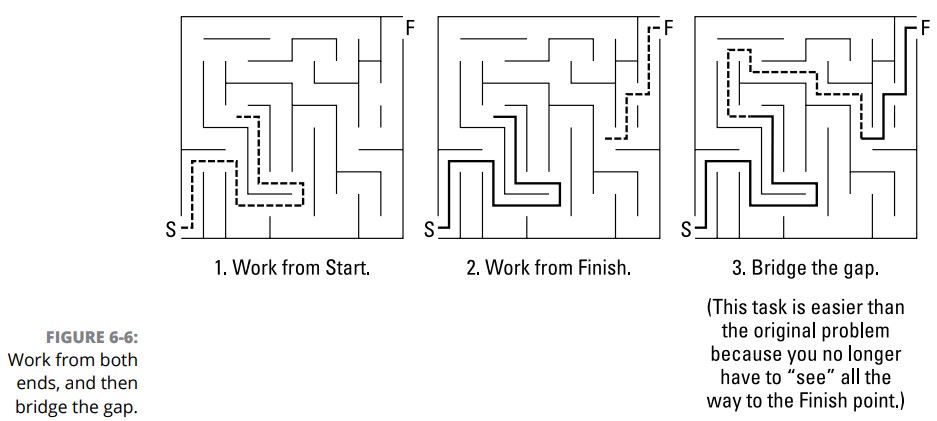
همانطور که در بخش قبلی توضیح دادم، کار کردن رو به سمت عقب از انتهای یک اثبات استراتژی خوبی است. شما همواره نمی توانید تا جایی که من در این اثبات رو به عقب کار کردم، کار کنید ـــ گاهی اوقات فقط می توانید تا گزارۀ یکی مانده به آخر برسید یا شاید دو تا مانده به آخر. اما اگر تنها یک یا دو گزاره (علاوه بر گزارۀ اتوماتیک آخر) را پر کنید، آن گزاره های افزوده شده می توانند بسیار سودمند باشند. بعد از ایجاد این اضافات، تمام کردن این اثبات ساده تر می شود زیرا مقصد نهایی جدیدِ شما (به عنوان مثال گزینۀ دو تا مانده به آخر)، مراحل کمتری تا آغاز اثبات دارد و از این رو هدف ساده تری برای دستیابی می باشد. به نوعی شبیه یکی از آن مسیرهای پر پیچ و خم می باشد که در مجلات و روزنامه ها می بینید: شما می توانید از شروع آن کار کنید؛ سپس، اگر گیر کردید، می توانید از آخر آن کار کنید. در پایان، شما می توانید به جایی در مسیر که از آنجا کار را متوقف کرده بودید باز گردید و به سادگی آن را به بخش پایانی متصل سازید. شکل 6-6 این فرآیند را به شما نشان می دهد.
اوکی، اگر این اثبات را تمام کنم، چه خواهید گفت؟ تمام چیزی که باقیمانده است، اینست که فاصلۀ بین گزارۀ 5 ، یعنی \(\angle{3} \cong \angle{4}\) ، و گزارۀ سه تا مانده به آخر، یعنی \(\angle{5} \cong \angle{6}\) را پر کنیم و آنها را به هم متصل سازیم. در اینجا دو داده داریم که هنوز از آنها استفاده نکرده اید، بنابراین آنها باید کلید تمام کردن این اثبات باشند.
چگونه می توانید از داده های مربوط به دو جفت از زاویه های متمم، استفاده کنید؟ شما ممکن است بخواهید دوباره سعی کنید از ایدۀ جایگذاری اعداد استفاده کنید. اعدادی مشابه اعداد قبلی را انتخاب کنید و فرض کنید که زاویه های همنهشتِ \(\angle{3}\) و \(\angle{4}\) هر دو \(55^{\circ}\) باشند. زاویۀ \(5\) متمم \(\angle{3}\) ، می باشد، بنابراین اگر \(\angle{3}\) \(55^{\circ}\) باشد، \(\angle{5}\) باید \(35^{\circ}\) باشد. زاویۀ \(6\) متمم \(\angle{4}\) می باشد، بنابراین \(\angle{6}\) نیز \(35^{\circ}\) می شود. درسته: \(\angle{5}\) و \(\angle{6}\) همنهشت هستند، و شما جزئیات تمام نشده را به یکدیگر متصل کردید. تنها چیز باقیمانده اینست که نوشتن اثبات رسمی را خاتمه دهید، که آن را در بخش بعدی برای شما انجامش داده ام.
راستی، استفاده از اندازۀ زاویه ها مانند این، یک استراتژی عالی می باشد، اما گاهی اوقات ضرورتی ندارد. اگر شما قضایا را بخوبی بدانید، ممکن است به سادگی بفهمید که از آنجا که \(\angle{3}\) و \(\angle{4}\) همنهشت هستند، متمم های آنها (\(\angle{5}\) و \(\angle{6}\)) باید همنهشت باشند.
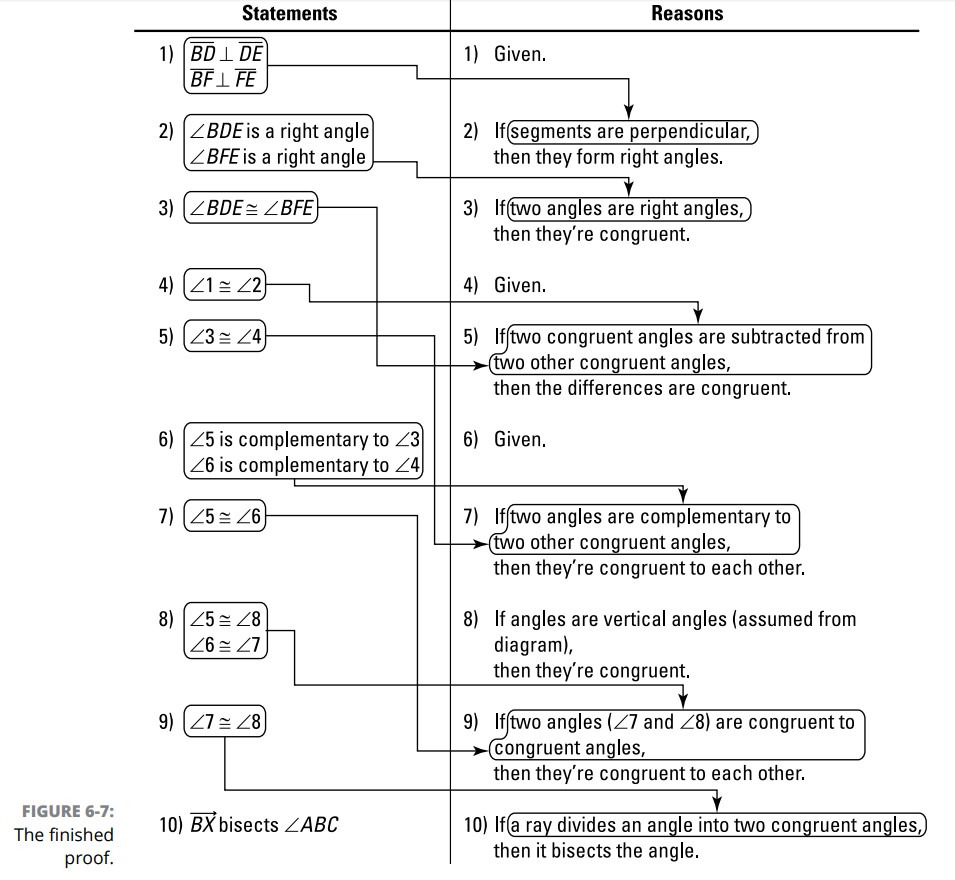
شیپورها را به صدا درآورید! در اینجا اثبات نهایی را با نشان دادن جریان منطق توسط حباب ها داریم (شکل 7-6 را ببینید). (این بار فلش ها را فقط برای متصل کردن جزء if به هر دلیل ترسیم کرده ام. شما می دانید که جزء then در هر دلیل باید به گزارۀ موجود در همان خط متصل گردد.) اگر شما تمامی استراتژیها و نکات پوشش داده شده در این فصل را درک کنید و بتوانید هر مرحله از این اثبات را دنبال کنید، باید قادر باشید تا تقریباً هر اثبات دیگری را که با آن مواجه می شوید، مدیریت کنید و از عهده اش بر بیایید.

اثباتی که برای این فصل ایجاد کرده ام، خیلی مشکل نیست؛ فقط از اثبات هایی که در فصل 5 دیدید، طولانی تر می باشد.

داده ها:
\(\overline{BD} \bot \overline{DE}\)
\(\overline{BF} \bot \overline{EF}\)
\(\angle{1} \cong \angle{2}\)
\(\angle{5}\) متمم \(\angle{3}\) می باشد
\(\angle{6}\) متمم \(\angle{4}\) می باشد
اثبات کنید:
\(\overrightarrow{BX}\) ، \(\angle{ABC}\) را تنصیف می کند
ایجاد یک استراتژی بازی
یک روش خوب برای آغاز هر اثباتی اینست که یک استراتژی بازی (game plan)، یا طرح کلی حدسی، از چگونگی انجام اثبات بسازید. روش رسمی نوشتن یک اثبات دو ستونی، مخصوصاً در ابتدا می تواند مشکل باشد ـــ تقریباً شبیه یادگیری یک زبان خارجی می باشد. اگر یک اثبات را به دو یا چند بخش کوتاه تر و قابلیت مدیریت تر بشکنید، نوشتن آن ساده تر می شود.
در ابتدا، شما یک استراتژی بازی را می نویسید یا به سادگی آن را در نظر می گیرید، که در آن شما با عقل و درایت خودتان، و بدون اینکه با نگارش صحیح زبان فنی درگیر گردید، وارد منطق اثبات می شوید. هنگامی که این کار را انجام دادید، گام دوم یعنی ترجمۀ این منطق به شکل دو ستونی زیاد سخت نخواهد بود.
همانطور که در فصل 5 دیدید، هنگامی که در مراحل استراتژی بازی هستید، گاهی اوقات ایدۀ خوبی است که اعداد دلخواهی را برای پاره خطها و زاویه ها در داده ها و برای پاره خطها و زاویه های نامبرده نشده، بسازید. با این حال، شما نباید برای پاره خطها و زاویه هایی که سعی بر همنهشت نشان دادن آنها دارید، اعدادی را بسازید. این مرحلۀ اختیاری شکل هندسی را مستحکم تر خواهد کرد و درک و توانایی مدیریت چگونگی اثبات را برای شما ساده تر خواهد ساخت.
در اینجا یک استراتژی بازیِ ممکن برای اثباتی که مشغول کار با آن هستیم را می بینید: داده های این اثبات برای شما دو جفت از پاره خطهای متعامد را تدارک دیده اند؛ که به شما \(90^{\circ}\) برای \(\angle{BDE}\) و \(\angle{BFE}\) را می دهد. سپس، فرض کنید زوایای همنهشت \(\angle{1}\) و \(\angle{2}\) هر دو برابر با \(30^{\circ}\) باشند. این منجر می شود تا \(\angle{3}\) و \(\angle{4}\) هر دو برابر با \(90^{\circ} - 30^{\circ}\) یا \(60^{\circ}\) گردند. سپس، از آنجا که \(\angle{3}\) و \(\angle{5}\)، همچنین \(\angle{4}\) و \(\angle{6}\) متمم هستند، \(\angle{5}\) و \(\angle{6}\) هر دو باید \(30^{\circ}\) باشند. زاویه های \(5\) و \(8\) و همچنین \(\angle{6}\) و \(\angle{7}\)، زوایای متقابل به رأس می باشند، بنابراین \(\angle{7}\) و \(\angle{8}\) نیز باید \(30^{\circ}\) باشند ـــ و از این رو آنها همنهشت می باشند. در آخر، از آنجا که \(\angle{7} \cong \angle{8}\) ، در نتیجه \(\angle{ABC}\) تنصیف شده است. تمام شد.
اگر همانطور که در مراحل استراتژی بازی پیش می روید، در دنبال کردن زنجیرۀ منطق ها مشکل دارید، همینطور که در هر مرحلۀ منطقی پیش می روید، شاید بخواهید علامتهایی رار بر روی شکل هندسی اثبات قرار دهید. به عنوان مثال، هرگاه که نتیجه گرفتید یک جفت پاره خط یا زاویه همنهشت می باشند، می توانید این همنهشتی را با قرار دادن علامت تیک بر روی شکل هندسی نشان بدهید. نشان دار کردن شکل هندسی به شما یک روش بصری سریع برای دنبال کردن دلایلتان می دهد.
هنگام انجام یک اثبات، با دقت در نظر گرفتن نتایج طرح اولیۀ استدلالهای اثبات، همانند استراتژی بازی پیشین، همیشه ایدۀ خوبی است. اگرچه، احتمالاً مواقعی باشد که شما نتوانید کل استدلال را فوراً متوجه شوید. اگر این اتفاق برای شما بیفتد، شما می توانید از استراتژی هایی که در بقیۀ این فصل ارائه شده اند تا به جنبه های مختلف اثبات فکر کنید. همچنین بخشهایی که به زودی خواهید دید، برخی نکات را برای شما فراهم آورده اند، که می توانند به شما کمک کنند اسکلت اصلیِ استراتژی بازی را به شکل یک اثبات دو ستونی تصحیح کنید.
استفاده از همۀ داده ها
شاید شما استراتژی بازی موجود در بخش قبل را دنبال نکنید ـــ یا شما آن را درک کرده اید اما فکر نمی کنید که خودتان قادر باشید به آن نتایج در نگاه اول برسید ـــ بنابراین شما به اثبات خیره شده اید و نمی دانید از کجا باید آغاز کنید. توصیۀ من: تمامی داده های اثبات را بررسی کنید و از خودتان بپرسید، چرا آنها هر داده ای را به شما داده اند.
هر داده ای یک راهنمای جاسازی شده می باشد.
به پنج دادۀ این اثبات نگاه کنید. فوراً آشکار نمی شود که سومین، چهارمین، و پنجمین داده چگونه می توانند به شما کمک کنند، اما در مورد دو دادۀ اول، یعنی پاره خطهای متعامد، چطور؟ چرا آنها باید این داده ها را به شما بدهند؟ خطهای متعامد چه چیزی را به شما می دهند؟ قطعاً، زوایه های قائمه. اوکی، بنابراین شما مسیر حرکت خودتان را پیدا کرده اید ـــ اکنون دو خط اول از اثبات را می دانید (شکل 1-6 را ببینید).

ترجمۀ شکل:
-
\(\overline{BD} \bot \overline{DE}\)
\(\overline{BF} \bot \overline{FE}\)
داده ها.
-
\(\angle{BDE}\) یک زاویۀ قائمه می باشد.
\(\angle{BFE}\) یک زاویۀ قائمه می باشد.
اگر پاره خطها متعامد باشند، سپس آنها یک زاویۀ قائمه را شکل می دهند.
توجه داشته باشید که اگر بدانید چگونه ساختار if-then در دلایل کار می کند، دومین دلیل تقریباً خودش را می نویسد (برای اطلاعات بیشتر در مورد منطق if-then بخش بعدی و همینطور فصل 4 را ببینید).
مطمئن شوید که از منطق If-Then استفاده می کنید
حرکت از داده ها به نتیجه گیریهای نهایی در یک اثبات دو ستونی به نوعی شبیه ضربه زدن به یک ردیف در دومینو می باشد. هر گزاره، مانند هر دومینو، به گزارۀ بعدی ضربه می زند (اگرچه، برخلاف دومینوها، یک گزاره همیشه به یکی بعد از خودش ضربه نمی زند). ساختار جملۀ if-then از هر دلیل در یک اثبات دو ستونی به شما نشان می دهد چگونه هر گزاره به گزارۀ بعدی ضربه می زند. به عنوان مثال، در شکل 1-6 دلیل "اگر دو پاره خط متعامد باشند، سپس آنها یک زاویۀ قائمه را تشکیل می دهند." را در نظر بگیرید، دومینوی متعامد (گزارۀ 1) به دومینوی زاویۀ قائمه ضربه می زند (گزارۀ 2). در شکل 2-6 ، یک خط دیگر به این اثبات اضافه می شود. دلیل 3 به شما توضیح می دهد که چگونه دومینوی زاویۀ قائمه (گزارۀ 2) به دومینویِ زاویه های همنهشت (گزارۀ 3)، ضربه می زند. این فرآیند در سراسر اثبات ادامه می یابد، اما، همانطور که پیشتر اشاره شد، همواره به این سادگی نیست که 1 به دو ضربه بزند، 2 به 3، 3 به 4، و به همین ترتیب. گاهی اوقات شما به دو گزاره نیاز دارید تا به گزارۀ دیگری ضربه بزنند، و گاهی اوقات شما گزاره ها را نادیده می گیرید؛ به عنوان مثال، در اثبات دیگری، گزارۀ 3 ممکن است به گزارۀ 5 ضربه بزند. تمرکز بر روی منطق if-then از یک اثبات، به شما کمک می کند تا ببینید چگونه کل اثبات به یکدیگر متصل می شوند.
مطمئن شوید که ساختار if-then در دلایل شما صحیح باشند (در مورد ساختار if-then در فصل 4 جزئیات بیشتری را پوشش داده ام):
-
مفهوم یا مفاهیم موجود در جزء If از یک دلیل باید در ستون گزاره جایی بالای آن خط از دلیل ظاهر شده باشد.
-
مفهوم موجود در جزء then از یک دلیل باید همان مفهوم موجود در گزاره ای باشد که مستقیماً در سمت مقابل دلیل قرار دارد.
یه شکل 1-6 بازگردید و نگاهی به آن بیندازید. از آنجا که تنها گزارۀ موجود در بالای دلیل 2، گزارۀ 1 می باشد، آنجا تنها جایی است که شما می توانید بدنبال مفاهیم موجود در جزء if از دلیل 2 بگردید. بنابراین، اگر شما این اثبات را با قرار دادن دو جفت از پاره خطهای متعامد در گزارۀ 1 آغاز کنید، سپس شما باید از آن اطلاعات در دلیل 2 استفاده نمایید، که باید اینطور آغاز شود "اگر پاره خطها متعامد باشند، سپس ...".
اکنون فرض کنید شما نمی دانید چه چیزی را باید در گزارۀ 2 قرار دهید. ساختار if-then از دلیل 2 به شما کمک می کند آن را بدانید. از آنجا که دلیل 2 اینگونه آغاز می شود "اگر دو پاره خط متعامد باشند ..." شما از خودتان می پرسید، "خوب، اگر دو خط متعامد باشند، چه اتفاقی می افتد؟" پاسخ، قطعاً، اینست که زاویه های قائمه تشکیل می شوند. بنابراین مفهوم زاویۀ قائمه باید در جزء then از دلیل 2 قرار گیرد و در گزارۀ دقیقاً مقابل آن یعنی گزارۀ 2 نیز قرار بگیرد.
اوکی، حالا چی؟ خوب، در مورد دلیل 3 فکر کنید. یک روش می تواند آغاز کردن با زاویه های قائمۀ موجود در گزارۀ 2 باشد. بخش if از دلیل 3 می تواند این باشد "اگر دو زاویه قائمه باشند ..." آیا می توانید این را تمام کنید؟ قطعاً: اگر دو زاویه قائمه باشند، سپس آنها همنهشت می باشند. بنابراین، انجام شد: شما دلیل 3 را یافتید، و گزارۀ 3 باید شامل مفهوم موجود در بخش then از دلیل 3 باشد، همنهشتی زاویه های قائمه. شکل 2-6 این اثبات را تا اینجایِ کار به شما نشان می دهد.

ترجمۀ شکل:
-
\(\overline{BD} \bot \overline{DE}\)
\(\overline{BF} \bot \overline{FE}\)
داده ها.
-
\(\angle{BDE}\) یک زاویۀ قائمه می باشد.
\(\angle{BFE}\) یک زاویۀ قائمه می باشد.
اگر پاره خطها متعامد باشند، سپس آنها یک زاویۀ قائمه را شکل می دهند.
-
\(\angle{BDE} \cong \angle{BFE}\)
اگر دو زاویه قائمه باشند، سپس با هم همنهشت می باشند.
هنگام نوشتن اثبات ها، شما نیاز دارید تا هر مرحلۀ کوچک را ساده کنید مانند اینکه مجبور باشید این منطق را برای یک کامپیوتر شفاف سازی کنید. به عنوان مثال، ممکن است بدیهی به نظر آید که اگر شما دو جفت خطهای متعامد داشته باشید، زاویه های همنهشت قائمه خواهید داشت، اما این نتیجه گیریِ ساده سه مرحله از یک اثبات دو ستونی را در بر می گیرد. شما باید از پاره خطهای متعامد به زاویه های قائمه و سپس به زاویه های قائمۀ همنهشت بروید ـــ شما نمی توانید سرراست به زاویه های قائمۀ همنهشت بپرید. این شیوه ای است که کامپیوتر تفکر می کند: \(A\) منجر به \(B\) می شود، \(B\) منجر به \(C\)، \(C\) منجر به \(D\)، و به همین ترتیب. شما باید هر حلقه در زنجیرۀ منطق را صراحتاً آشکار سازید.
خُرد کردن مسأله
با آن مواجه شوید: شما ممکن است در جایی از اثبات گیر کنید، یا خدای ناکرده، در چندین نقطۀ یک اثبات متوقف شوید! با خودتان بیندیشید وقتی گیر کردید، چه کار باید کنید؟
چیزی را امتحان کنید. هنگام انجام اثبات های هندسی، شما نیاز دارید تا ایده هایی را با آزمون و خطا امتحان کنید. انجام دادن اثبات به اندازه کارهای ریاضی که تا کنون انجام داده اید، سیاه و سفید نمی باشد. شما معمولاً به یقین نمی دانید چه چیزی درست کار خواهد کرد. فقط چیزی را امتحان کنید، و اگر درست کار نکرد، چیز دیگری را امتحان کنید. دیر یا زود، کلیت اثبات باید قابل درک گردد.
تا اینجایِ اثبات این فصل، شما دو زاویۀ همنهشت در گزارۀ 3 دارید، اما شما نمی توانید به تنهایی با این مفهوم بیش از این پیش بروید. بنابراین، داده ها را مجدداً بررسی کنید. کدامیک از سه دادۀ استفاده نشده ممکن است گزارۀ 3 را بسازد؟ هیچ روشی وجود ندارد که با اطمینان این سوال را پاسخ دهید، بنابراین شما نیاز دارید تا به غرایزتان اطمینان کنید، داده ای را انتخاب کنید، و آن را امتحان کنید (یا اگر فکر می کنید غریزه ای برای این کار ندارید، سپس فقط چیزی را امتحان کنید، هر چیزی می تواند باشد).
سومین داده به شما میگوید \(\angle{1} \cong \angle{2}\) . این امیدوارکننده به نظر می رسد زیرا زاویه های \(1\) و \(2\) بخشی از زاویه های قائمۀ موجود در گزارۀ 3 می باشند. شما می توانید از خودتان بپرسید، "اگر \(\angle{1}\) و \(\angle{2}\) به عنوان مثال برابر با \(35^{\circ}\) باشند، به دنبال آن چه چیزی خواهد بود؟" شما می دانید که زاویه های قائمه \(90^{\circ}\) می باشند، بنابراین اگر \(\angle{1}\) و \(\angle{2}\) \(35^{\circ}\) باشند، \(\angle{3}\) و \(\angle{4}\) هر دو برابر با \(55^{\circ}\) خواهند بود و بنابراین، قطعاً، آنها همنهشت می باشند. درسته. شما در حال پیشرفت هستید. شما می توانید از آن دادۀ سوم در گزارۀ 4 استفاده کنید و سپس در گزارۀ 5 بیان کنید که \(\angle{3} \cong \angle{4}\) .
شکل 3-6 این اثبات را تا گزارۀ 5 نشان می دهد. حباب ها و فلش ها به شما نشان می دهند چگونه گزاره ها و دلایل به یکدیگر متصل هستند. شما می توانید ببینید که جزء if از هر دلیل به گزاره ای در بالای آن دلیل مرتبط است و جزء then به گزارۀ موجود در همان خط دلیل، مرتبط می باشد. از آنجا که من هنوز از دلیل 5 جلوتر نرفته ام، در شکل موجود نمی باشد. ببینید آیا می توانید قبل از اینکه توضیحاتی را که متعاقباً آمده است بخوانید، دلیل 5 را متوجه گردید. راهنما: بخش then از دلیل 5 باید با گزارۀ 5 که در شکل نشان داده شده است، مرتبط باشد.

ترجمۀ شکل:
-
\(\overline{BD} \bot \overline{DE}\)
\(\overline{BF} \bot \overline{FE}\)
داده ها.
-
\(\angle{BDE}\) یک زاویۀ قائمه می باشد.
\(\angle{BFE}\) یک زاویۀ قائمه می باشد.
اگر پاره خطها متعامد باشند، سپس آنها یک زاویۀ قائمه را شکل می دهند.
-
\(\angle{BDE} \cong \angle{BFE}\)
اگر دو زاویه قائمه باشند، سپس با هم همنهشت می باشند.
-
\(\angle{1} \cong \angle{2}\)
داده ها.
-
\(\angle{3} \cong \angle{4}\)
اگر ...... ، سپس .......... .
خوب، آیا دلیل 5 را متوجه شدید؟ پاسخ آن تفریق زاویه ها می باشد، با استفاده از اندازۀ \(35^{\circ}\) برای \(\angle{1}\) و \(\angle{2}\) ، به اندازۀ \(55^{\circ}\) برای \(\angle{3}\) و \(\angle{4}\) در گزارۀ 5 می رسیم، و شما این پاسخ \(55^{\circ}\) را با انجام یک تفریق، یعنی \(90^{\circ} - 35^{\circ}=55^{\circ}\) بدست می آورید. (این اشتباه را نکنید که فکر کنید این یک جمع زاویه ها می باشد زیرا \(35^{\circ} + 55^{\circ} = 90^{\circ}\) .) شما دو زاویه را از دو زاویۀ دیگر تفریق می کنید، بنابراین از نسخۀ چهار زاویه ای از تفریق زاویه ها استفاده می کنید (فصل 5 را ببینید). بنابراین دلیل 5 می شود "اگر دو زاویۀ همنهشت (\(\angle{1}\) و \(\angle{2}\)) از دو زاویۀ همنهشت دیگر (زاویه های قائمه) تفریق گردند، سپس تفاضل آنها (\(\angle{3}\) و \(\angle{4}\)) همنهشت می باشند."
اگر ندانید این پنج خط شما را به کجا می برند یا اینکه آنها صحیح هستند یا خیر، ممکن است اندکی (یا بیش از اندکی) نگران و مردد شوید. شما ممکن است از خودتان بپرسید "هدف از انجام این کار چیست" ، "اینکه پنج خط را انجام بدهم و در عین حال ندانم که باید به کجا بروم؟". این یک پاسخ و عکس العمل قابل درک است. پاسخش اینست.
اگر در وسط مراحل حل کردن یک اثبات باشید و ندانید چگونه باید به انتهای آن برسید، یادتان باشد که دنبال کردن مراحل چیز خوبی است. اگر بتوانید حقایق بیشتر و بیشتری را نتیجه گیری کنید و بتوانید ستون گزاره ها را پر کنید، به احتمال زیاد در مسیر درستی قرار دارید. در مورد این احتمال که ممکن است مسیر را اشتباه بروید، نگران نباشید. (هرچند اینگونه بیراهه ها ممکن است هر از گاهی رخ بدهند، نگران آنها نباشید. اگر به بُن بست رسیدید، فقط بازگردید و روش دیگری را امتحان کنید).
احساس نکنید مجبور هستید یک مرتبه به آخر کار برسید و ببنید که کل اثبات چگونه در کنار یکدیگر قرار می گیرد. در عوض، صرفاً به ایجاد یک گام رو به هدف خرسند و راضی باشید (یک گزارۀ بیشتر بدست آورید)، سپس گام بعدی، سپس بعدی، و به همین ترتیب. دیر یا زود به منطقۀ پایانی می رسید. یک بار در مورد دانش آموزی شنیدم که نمراتش در هندسه از C و D به نمرات A و B تغییر یافت، و تمامی این تغییرات فقط بخاطر تغییر تمرکز او از تمرکز بر روی رسیدن به پاسخ نهایی اثبات ها به تمرکز بر روی حرکت قدم به قدم برای حل اثبات بود.
پرش رو به سمت جلو و کار کردن رو به سمت عقب
فرض کنید در میانۀ یک اثبات هستید و نمی دانید چگونه باید از جایی که هستید به خط پایانی برسید. نگران نباشید ـــ فقط به آخر اثبات پرش کنید و از آنجا رو به عقب باز گردید.
اوکی، از جایی در اثبات این فصل که متوقف شده ایم دوباره از سر بگیرید: شما پنج خط از این اثبات را تکمیل کرده اید، و به \(\angle{3} \cong \angle{4}\) رسیده اید. حالا کجا باید بروید؟ پیش رفتن از اینجا ممکن است اندکی مهارت آمیز باشد، بنابراین رو به سمت عقب کار کنید. شما می دانید که در آخرین خط از این اثبات باید اثبات شود که: \(\overrightarrow{BX}\) ، \(\angle{ABC}\) را تنصیف می کند. اکنون اگر در مورد اینکه آخرین دلیل چه باید باشد، فکر کنید، یا در مورد اینکه گزارۀ یکی مانده به آخر چه باید باشد، مشکل نخواهد بود که بدانید نیاز به دو زاویۀ همنهشت دارید (دو زاویۀ نصف شده)، تا از روی آن استنتاج کنید که یک زاویۀ بزرگتر تنصیف شده است. شکل 4-6 به شما نشان می دهد آخر اثبات چگونه خواهد بود. به حباب های منطق if-then دقت کنید (جزء if در دلایل به گزارۀ بالای آن دلیل متصل است؛ جزء then در دلایل به گزارۀ موجود در همان خط دلیل متصل است).

ترجمۀ شکل:
-
.......
-
یکی مانده به آخر) \(\angle{7} \cong \angle{8}\)
-
آخرین) \(\overrightarrow{BX}\) ، \(\angle{ABC}\) را تنصیف می کند
اگر یک نیمخط زاویه ای را به دو زاویۀ همنهشت تقسیم کند، سپس آن زاویه را تنصیف کرده است.
برای ادامه دادن حرکت رو به سمت عقب و رسیدن به گزارۀ دو تا مانده به آخر، سه تا مانده به آخر، و به همین ترتیب، تلاش کنید. (حرکت رو به سمت عقب از میان یک اثبات همواره شامل برخی حدس ها خواهد بود، اما اجازه ندهید این شما را متوقف کند.) چرا ممکن است \(\angle{7}\) با \(\angle{8}\) همنهشت باشد؟ خوب، احتمالاً نیازی ندارید خیلی سخت بررسی کنید تا جفتی از زوایای متقابل به رأس همنهشت را بیابید، \(\angle{5}\) و \(\angle{8}\) ، و جفتی دیگر، \(\angle{6}\) و \(\angle{7}\).
اوکی، شما نیاز دارید تا نشان دهید که \(\angle{7}\) با \(\angle{8}\) همنهشت می باشد، و شما می دانید که \(\angle{6}\) با \(\angle{7}\) برابر می باشد، و \(\angle{5}\) با \(\angle{8}\) برابر می باشد. بنابراین اگر شما بدانید که زوایای \(\angle{5}\) و \(\angle{6}\) همنهشت می باشند، موفقیتتان قطعی خواهد بود.
حالا که چند مرحله رو به سمت عقب حرکت کردید، در اینجا استدلالی رو به سمت جلو داریم: این اثبات می تواند در گزارۀ سه تا مانده به آخر بیان کند \(\angle{5} \cong \angle{6}\) ، سپس در دو تا مانده به آخرین گزاره بیان دارد که \(\angle{5} \cong \angle{8}\) و \(\angle{6} \cong \angle{7}\) (زیرا زوایای متقابل به رأس با یکدیگر همنهشت می باشند)، و سپس در گزارۀ یکی مانده به آخر بیان کند که \(\angle{7} \cong \angle{8}\) (با استفاده از ویژگی تراگذری برای چهار زاویه. فصل 5 را ببینید). شکل 5-6 نشان می دهد تمامی اینها در شکل دو ستونی چگونه نوشته می شوند.

ترجمۀ شکل:
-
.......
-
سه تا مانده به آخر) \(\angle{5} \cong \angle{6}\)
؟؟؟
-
دو تا مانده به آخر) \(\angle{5} \cong \angle{8}\)
\(\angle{6} \cong \angle{7}\)
اگر زاویه ها متقابل به رأس باشند (از روی شکل هندسی مفروض شده است)، سپس آنها همنهشت هستند.
-
یکی مانده به آخر) \(\angle{7} \cong \angle{8}\)
-
آخرین) \(\overrightarrow{BX}\) ، \(\angle{ABC}\) را تنصیف می کند
اگر یک نیمخط زاویه ای را به دو زاویۀ همنهشت تقسیم کند، سپس آن زاویه را تنصیف کرده است.
پُر کردن جاهای خالی
همانطور که در بخش قبلی توضیح دادم، کار کردن رو به سمت عقب از انتهای یک اثبات استراتژی خوبی است. شما همواره نمی توانید تا جایی که من در این اثبات رو به عقب کار کردم، کار کنید ـــ گاهی اوقات فقط می توانید تا گزارۀ یکی مانده به آخر برسید یا شاید دو تا مانده به آخر. اما اگر تنها یک یا دو گزاره (علاوه بر گزارۀ اتوماتیک آخر) را پر کنید، آن گزاره های افزوده شده می توانند بسیار سودمند باشند. بعد از ایجاد این اضافات، تمام کردن این اثبات ساده تر می شود زیرا مقصد نهایی جدیدِ شما (به عنوان مثال گزینۀ دو تا مانده به آخر)، مراحل کمتری تا آغاز اثبات دارد و از این رو هدف ساده تری برای دستیابی می باشد. به نوعی شبیه یکی از آن مسیرهای پر پیچ و خم می باشد که در مجلات و روزنامه ها می بینید: شما می توانید از شروع آن کار کنید؛ سپس، اگر گیر کردید، می توانید از آخر آن کار کنید. در پایان، شما می توانید به جایی در مسیر که از آنجا کار را متوقف کرده بودید باز گردید و به سادگی آن را به بخش پایانی متصل سازید. شکل 6-6 این فرآیند را به شما نشان می دهد.

اوکی، اگر این اثبات را تمام کنم، چه خواهید گفت؟ تمام چیزی که باقیمانده است، اینست که فاصلۀ بین گزارۀ 5 ، یعنی \(\angle{3} \cong \angle{4}\) ، و گزارۀ سه تا مانده به آخر، یعنی \(\angle{5} \cong \angle{6}\) را پر کنیم و آنها را به هم متصل سازیم. در اینجا دو داده داریم که هنوز از آنها استفاده نکرده اید، بنابراین آنها باید کلید تمام کردن این اثبات باشند.
چگونه می توانید از داده های مربوط به دو جفت از زاویه های متمم، استفاده کنید؟ شما ممکن است بخواهید دوباره سعی کنید از ایدۀ جایگذاری اعداد استفاده کنید. اعدادی مشابه اعداد قبلی را انتخاب کنید و فرض کنید که زاویه های همنهشتِ \(\angle{3}\) و \(\angle{4}\) هر دو \(55^{\circ}\) باشند. زاویۀ \(5\) متمم \(\angle{3}\) ، می باشد، بنابراین اگر \(\angle{3}\) \(55^{\circ}\) باشد، \(\angle{5}\) باید \(35^{\circ}\) باشد. زاویۀ \(6\) متمم \(\angle{4}\) می باشد، بنابراین \(\angle{6}\) نیز \(35^{\circ}\) می شود. درسته: \(\angle{5}\) و \(\angle{6}\) همنهشت هستند، و شما جزئیات تمام نشده را به یکدیگر متصل کردید. تنها چیز باقیمانده اینست که نوشتن اثبات رسمی را خاتمه دهید، که آن را در بخش بعدی برای شما انجامش داده ام.
راستی، استفاده از اندازۀ زاویه ها مانند این، یک استراتژی عالی می باشد، اما گاهی اوقات ضرورتی ندارد. اگر شما قضایا را بخوبی بدانید، ممکن است به سادگی بفهمید که از آنجا که \(\angle{3}\) و \(\angle{4}\) همنهشت هستند، متمم های آنها (\(\angle{5}\) و \(\angle{6}\)) باید همنهشت باشند.
نوشتن اثبات نهایی
شیپورها را به صدا درآورید! در اینجا اثبات نهایی را با نشان دادن جریان منطق توسط حباب ها داریم (شکل 7-6 را ببینید). (این بار فلش ها را فقط برای متصل کردن جزء if به هر دلیل ترسیم کرده ام. شما می دانید که جزء then در هر دلیل باید به گزارۀ موجود در همان خط متصل گردد.) اگر شما تمامی استراتژیها و نکات پوشش داده شده در این فصل را درک کنید و بتوانید هر مرحله از این اثبات را دنبال کنید، باید قادر باشید تا تقریباً هر اثبات دیگری را که با آن مواجه می شوید، مدیریت کنید و از عهده اش بر بیایید.

ترجمۀ شکل:
-
\(\overline{BD} \bot \overline{DE}\)
\(\overline{BF} \bot \overline{FE}\)
داده ها.
-
\(\angle{BDE}\) یک زاویۀ قائمه می باشد.
\(\angle{BFE}\) یک زاویۀ قائمه می باشد.
اگر پاره خطها متعامد باشند، سپس آنها یک زاویۀ قائمه را شکل می دهند.
-
\(\angle{BDE} \cong \angle{BFE}\)
اگر دو زاویه قائمه باشند، سپس با هم همنهشت می باشند.
-
\(\angle{1} \cong \angle{2}\)
داده ها.
-
\(\angle{3} \cong \angle{4}\)
اگر دو زاویۀ همنهشت از دو زاویۀ همنشهت دیگر تفریق گردند ، سپس تفاضل آنها همنهشت خواهند بود.
-
\(\angle{5}\) متمم \(\angle{3}\) می باشد
\(\angle{6}\) متمم \(\angle{4}\) می باشد
داده ها.
-
\(\angle{5} \cong \angle{6}\)
اگر دو زاویه متمم دو زاویۀ همنهشت دیگر باشند، سپس آنها متمم یکدیگر می باشند.
-
\(\angle{5} \cong \angle{8}\)
\(\angle{6} \cong \angle{7}\)
اگر زاویه ها متقابل به رأس باشند (از روی شکل هندسی مفروض شده است)، سپس آنها همنهشت هستند.
-
\(\angle{7} \cong \angle{8}\)
-
\(\overrightarrow{BX}\) ، \(\angle{ABC}\) را تنصیف می کند
اگر یک نیمخط زاویه ای را به دو زاویۀ همنهشت تقسیم کند، سپس آن زاویه را تنصیف کرده است.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: