خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
انواع مثلث بر اساس ضلع

مثلث (triangle) به نوعی کوچکترین عضو خانوادۀ چندضلعی ها (polygon) می باشد، قطعاً مثلث نقش مهمی در هندسه بازی می کند. مثلث ها یکی از مهمترین اجزاء در اثباتهای هندسی می باشند (اثباتهای مثلث را در فصل 9 خواهید دید). همچنین مثلثها دارای تعداد زیادی از ویژگیهای جالب می باشند که ممکن است شما از ساده ترین چندضلعیِ ممکن انتظارش را نداشته باشید. شاید لئوناردو داوینچی (Leonardo da Vinci) وقتی که گفت: "سادگی نهایت پیچیدگی می باشد."، چیزی می دانسته است.

در این فصل، من اصول اولیه مثلث ها را به شما توضیح می دهم ـــ اسامی آنها، ضلع ها ، زاویه ها، و مساحت. همچنین چگونگی یافتن چهار مرکز (centers) یک مثلث را به شما نشان می دهم.
مثلث ها بر اساس اندازۀ اضلاعشان یا اندازۀ زاویه هایشان دسته بندی شده اند. این دسته بندی ها در سه نوع موجودند، درست شبیه خود اضلاع و زاویه ها. این یعنی، یک مثلث دارای سه ضلع، و سه اصطلاح که مثلث ها را بر اساس اضلاعشان توصیف می کنند، می باشد؛ همچنین یک مثلث دارای سه زاویه می باشد، و سه دسته بندی بر اساس زاویه ها. در مورد دسته بندی مبتنی بر زاویه ها در بخشهای بعدی صحبت خواهم کرد.
در ادامه دسته بندیهای مثلث ها بر اساس اضلاعشان را می بینید:
از آنجا که یک مثلث متساوی الاضلاع، متساوی الساقین نیز می باشد، همۀ مثلث ها یا مختلف الاضلاع یا متساوی الساقین هستند. اما هنگامی که افراد مثلثی را متساوی الساقین می نامند، معمولاً اشارۀ آنها به مثلثی است که فقط دو ضلع برابر دارد، زیرا اگر مثلثی دارای سه ضلع برابر باشد، آن را متساوی الاضلاع می نامند. خوب، آیا سه نوع مثلث داریم یا فقط دو نوع؟ خودتان قضاوت کنید.
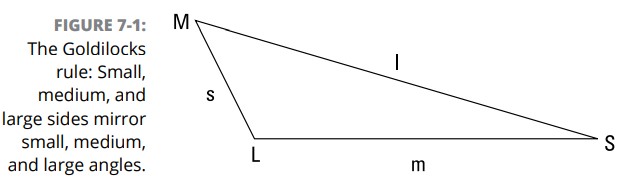
مثلث های مختلف الاضلاع، علاوه بر اینکه دارای سه ضلع نابرابر هستند، سه زاویۀ نابرابر نیز دارند. کوتاهترین ضلع در مقابل کوچکترین زاویه قرار دارد، ضلع میانی مقابل زاویۀ میانی قرار دارد، و ـــ سورپرایز، سورپرایز ـــ بزرگترین ضلع در مقابل بزرگترین زاویه می باشد. شکل 1-7 منظور من را به شما نشان می دهد.
یک مثلث متساوی الساقین دارای دو ضلع برابر و دو زاویۀ برابر می باشد. اضلاع برابر آن ساقها (legs)، و ضلع سوم آن قاعده (base) نامیده می شود ـــ به ضلع سوم پایه نیز گفته می شود. دو زاویه ای که قاعده را لمس می کنند (که همنهشت یا برابر هستند) زاویه های مجاور به قاعده (base angles) نامیده می شوند. زاویۀ بین دو ساق، زاویۀ رأس (vertex angle) نامیده می شود. شکل 2-7 را ببینید.
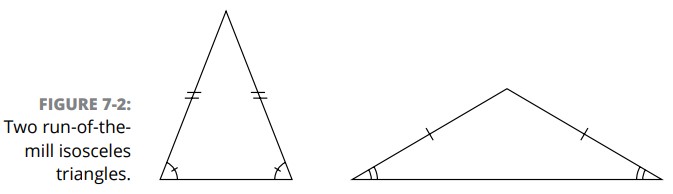
یک مثلث متساوی الاضلاع دارای سه ضلع برابر و سه زاویۀ برابر می باشد (که همگی \(60^{\circ}\) می باشند). زاویای برابر آن چیزی شبیه متساوی الاضلاع، با نام متساوی الزوایا (equiangular) می سازد. با این حال، شما معمولاً عبارت متساوی الزوایا را نخواهید شنید، زیرا تنها مثلث متساوی الزاویا، مثلث متساوی الاضلاع می باشد، و همه این نوع مثلث ها را متساوی الاضلاع می نامند. (با این وجود، در مورد چهار ضلعی ها و سایر انواع چندضلعی ها، شما به هر دوی این اصطلاحات نیاز خواهید داشت، زیرا یک شکل متساوی الزاویا، مانند یک مستطیل، می تواند دارای اضلاعی با اندازه های متفاوت باشد، و یک شکل متساوی الاضلاع، مانند لوزی، می تواند زوایایی با اندازه های متفاوت داشته باشد. برای جزئیات بیشتر فصل 12 را ببینید.)
اگر یک مثلث متساوی الاضلاع را مستقیماً از وسط آن به دو نیم کنید، شما دو مثلث با زاوایای \(30^{\circ}-60^{\circ}-90^{\circ}\) بدست می آورید. در فصل بعد خواهید دید که این مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) فوق العاده مهم می باشد.

در این فصل، من اصول اولیه مثلث ها را به شما توضیح می دهم ـــ اسامی آنها، ضلع ها ، زاویه ها، و مساحت. همچنین چگونگی یافتن چهار مرکز (centers) یک مثلث را به شما نشان می دهم.
در نظر گرفتن اضلاع مثلث ها
مثلث ها بر اساس اندازۀ اضلاعشان یا اندازۀ زاویه هایشان دسته بندی شده اند. این دسته بندی ها در سه نوع موجودند، درست شبیه خود اضلاع و زاویه ها. این یعنی، یک مثلث دارای سه ضلع، و سه اصطلاح که مثلث ها را بر اساس اضلاعشان توصیف می کنند، می باشد؛ همچنین یک مثلث دارای سه زاویه می باشد، و سه دسته بندی بر اساس زاویه ها. در مورد دسته بندی مبتنی بر زاویه ها در بخشهای بعدی صحبت خواهم کرد.
در ادامه دسته بندیهای مثلث ها بر اساس اضلاعشان را می بینید:
-
مثلث مختلف الاضلاع (Scalene triangle): یک مثلث مختلف الاضلاع، مثلثی است که هیچکدام از اضلاعش با هم همنهشت نیستند.
-
مثلث متساوی الساقین (Isosceles triangle): یک مثلث متساوی الساقین، مثلثی است که دست کم دو تا از اضلاعش با هم همنهشت باشند.
-
مثلث متساوی الاضلاع (Equilateral triangle): یک مثلث متساوی الاضلاع، مثلثی است که هر سه ضلع آن با هم همنهشت هستند.
از آنجا که یک مثلث متساوی الاضلاع، متساوی الساقین نیز می باشد، همۀ مثلث ها یا مختلف الاضلاع یا متساوی الساقین هستند. اما هنگامی که افراد مثلثی را متساوی الساقین می نامند، معمولاً اشارۀ آنها به مثلثی است که فقط دو ضلع برابر دارد، زیرا اگر مثلثی دارای سه ضلع برابر باشد، آن را متساوی الاضلاع می نامند. خوب، آیا سه نوع مثلث داریم یا فقط دو نوع؟ خودتان قضاوت کنید.
مثلث مختلف الاضلاع (Scalene)
مثلث های مختلف الاضلاع، علاوه بر اینکه دارای سه ضلع نابرابر هستند، سه زاویۀ نابرابر نیز دارند. کوتاهترین ضلع در مقابل کوچکترین زاویه قرار دارد، ضلع میانی مقابل زاویۀ میانی قرار دارد، و ـــ سورپرایز، سورپرایز ـــ بزرگترین ضلع در مقابل بزرگترین زاویه می باشد. شکل 1-7 منظور من را به شما نشان می دهد.

نسبت (ratio) اضلاع با نسبت زاویه ها برابر نمی باشند. فرض نکنید که به عنوان مثال، اگر یکی از اضلاع مثلث دوبرابر ضلع دیگر باشد، زاویه های مقابل آن این اضلاع نیز دارای نسبت \(2:1\) باشند. نسبت اضلاع ممکن است به نسبت زاویه ها نزدیک باشد، اما این نسبت ها هرگز دقیقاً برابر نیستند (مگر اینکه اضلاع با هم برابر باشند).
اگر سعی دارید تا چیزی در مورد مثلث ها بفهمید ـــ مانند اینکه آیا نیمساز (bisector) یک زاویه، اضلاع مقابلش را تنصیف می کند ـــ می توانید یک مثلث بکشید و بررسی کنید که آیا این مسأله صحیح می باشد یا خیر. اما مثلثی که ترسیم می کنید باید یک مثلث مختلف الاضلاعِ غیر قائم الزاویه باشد (مخالف یک مثلث متساوی الساقین، متساوی الاضلاع، یا قائم الزاویه باشد). این از آن جهت است که مثلث های مختلف الاضلاع، بنا به تعریفشان، فاقد ویژگیهای خاص همچون اضلاع همنهشت یا زاویه های قائمه می باشند. اگر مثلثی ترسیم کنید، فرض کنید به جای آن یک مثلث متساوی الساقین ترسیم کنید، هر نتیجه گیری که به آن برسید ممکن است برای آن نوع مثلث خاص صحیح باشد. به طور کلی، در هر ناحیه ای از ریاضی، هنگامی که می خواهید در مورد مفاهیمی تحقیق کنید، نباید چیزها را بیش از آن چیزی که باید باشند، خاص در نظر بگیرید.
مثلث متساوی الساقین (Isosceles)
یک مثلث متساوی الساقین دارای دو ضلع برابر و دو زاویۀ برابر می باشد. اضلاع برابر آن ساقها (legs)، و ضلع سوم آن قاعده (base) نامیده می شود ـــ به ضلع سوم پایه نیز گفته می شود. دو زاویه ای که قاعده را لمس می کنند (که همنهشت یا برابر هستند) زاویه های مجاور به قاعده (base angles) نامیده می شوند. زاویۀ بین دو ساق، زاویۀ رأس (vertex angle) نامیده می شود. شکل 2-7 را ببینید.

مثلث متساوی الاضلاع (Equilateral)
یک مثلث متساوی الاضلاع دارای سه ضلع برابر و سه زاویۀ برابر می باشد (که همگی \(60^{\circ}\) می باشند). زاویای برابر آن چیزی شبیه متساوی الاضلاع، با نام متساوی الزوایا (equiangular) می سازد. با این حال، شما معمولاً عبارت متساوی الزوایا را نخواهید شنید، زیرا تنها مثلث متساوی الزاویا، مثلث متساوی الاضلاع می باشد، و همه این نوع مثلث ها را متساوی الاضلاع می نامند. (با این وجود، در مورد چهار ضلعی ها و سایر انواع چندضلعی ها، شما به هر دوی این اصطلاحات نیاز خواهید داشت، زیرا یک شکل متساوی الزاویا، مانند یک مستطیل، می تواند دارای اضلاعی با اندازه های متفاوت باشد، و یک شکل متساوی الاضلاع، مانند لوزی، می تواند زوایایی با اندازه های متفاوت داشته باشد. برای جزئیات بیشتر فصل 12 را ببینید.)
اگر یک مثلث متساوی الاضلاع را مستقیماً از وسط آن به دو نیم کنید، شما دو مثلث با زاوایای \(30^{\circ}-60^{\circ}-90^{\circ}\) بدست می آورید. در فصل بعد خواهید دید که این مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) فوق العاده مهم می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: