خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
یافتن مراکز یک مثلث

در این بخش، چهار نقطه را که در ارتباط با هر مثلثی می باشند، بررسی می کنیم. یکی از این نقاط مرکز ثقل هندسی (centroid) نامیده می شود، و سه نقطۀ دیگر مراکز (centers) نامیده می شوند، اما هیچکدام از آنها مرکز واقعیِ یک مثلث نمی باشند. برخلاف دایره ها، مربع ها، و مستطیل ها، در مثلث ها (به جز مثلث متساوی الاضلاع) مرکز واقعی وجود ندارد.

قبل از اینکه مرکز ثقل هندسی را برای شما تعریف کنم، ابتدا نیاز به تعریف اصطلاح دیگری دربارۀ مثلث ها دارید: میانه (median).
در هر میانه، فاصلۀ بین رأس تا مرکز ثقل هندسی دوبرابر فاصلۀ مرکز ثقل هندسی تا نقطۀ میانی می باشد. شکل 10-7 را ببینید.
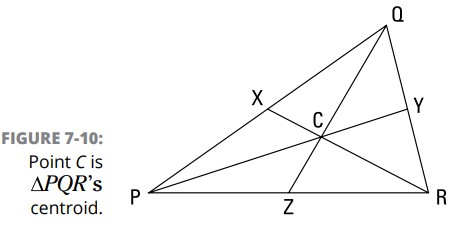
\(X\) ، \(Y\) ، و \(Z\) نقاط میانی اضلاعِ \(\triangle{PQR}\) می باشند؛ \(\overline{RX}\) ، \(\overline{PY}\) ، و \(\overline{QZ}\) میانه ها می باشند؛ و این میانه ها در نقطۀ \(C\)، یعنی مرکز ثقل هندسی، یکدیگر را قطع می کنند. اگر خط کشتان را بیرون بکشید (یا فقط از انگشتانتان استفاده کنید)، می توانید بررسی کنید که مرکز ثقل هندسی در \({1\over3}\) میانه ها ، به عنوان مثال \(\overline{PY}\)، می باشد. به عبارت دیگر \(\overline{CY}\) برابر با \({1\over3}\) \(\overline{PY}\) می باشد (بنابراین \(\overline{CY}\) نصفِ \(\overline{CP}\) می باشد).
شما احتمالاً بخواهید تا واقعاً ببینید چگونه یک مثلث در مرکز ثقلش تعادل خواهد داشت. یک مثلث را در هر شکلی از یک تکه مقوای نسبتاً سفت و سخت برش دهید. با قدت نقطۀ میانی دو تا از ضلع های آن را بیابید، و سپس دو تا از میانه ها را به آن نقاط ترسیم کنید. جایی که این دو میانه همدیگر را قطع می کنند، مرکز ثقل هندسی این مثلث است (اگر بخواهید می توانید میانه سوم را نیز ترسیم کنیم، اما برای یافتن مرکز ثقل هندسی مثلث همان دو میانه کفایت خواهد کرد). حالا از چیزی با نوک مسطح و کوچک همچون یک مداد تراشیده نشده استفاد کنید، اگر مستقیماً مرکز ثقل را بر روی سطح صاف انتهای این مداد تراشیده نشده قرار دهید، مثلث تعادل خودش را حفظ خواهد کرد.
مرکز ثقل هندسیِ یک مثلث احتمالاً به عنوان یک نقطۀ خوب است که به شما محل تخمینی مرکز مثلث را بگوید. این مرکز ثقل هندسی قطعاً کاندیدای بهتری برای مرکزیت یک مثلث می باشد، بهتر از سه نقطه ای که در ادامه در موردشان بحث خواهم کرد.
علاوه بر مرکز ثقل هندسی، هر مثلثی سه مرکز (centers) دیگر هم دارد که در محل تقاطع نیمخطها، خطها، و پاره خطهای مرتبط با این مثلث قرار گرفته اند.
شما مرکز دایره محاطی یک مثلث را در محل تقاطع سه نیمساز زوایای آن مثلث می یابید. این محل به مرکز دایره محاطی یک ویژگی جالب می دهد: مرکز دایره محاطی از هر سه ضلع یک مثلث در یک فاصلۀ برابر قرار دارد. هیچ نقطۀ دیگری این کیفیت را ندارد. مراکز دایره محاطی، همانند مراکز ثقل هندسی، همواره درون مثلث هایشان قرار دارند.
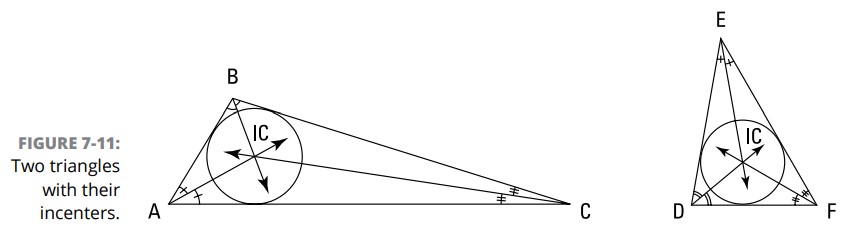
شکل 11-7 دو مثلث را با مراکز دایره محیطی شان و دایره های محاطی شان (inscribed circles)، نشان می دهد. (دایره های محاطی درون مثلث ها ترسیم می شوند، بنابراین این دایره ها به سختی اضلاع هر مثلث را لمس می کنند). مراکز دایره محاطی، مراکز این دایره های محاطی می باشند.
شما مرکز دایره محیطی یک مثلث را در محل تقاطع نیم ساز های عمود اضلاع آن می یابید. این محل به مرکز دایره محیطی یک ویژگی جالب می دهد: مرکز دایره محیطی از هر سه رأس یک مثلث فاصلۀ یکسانی دارد.
شکل 12-7 دو مثلث را همراه با مراکز دایره محیطی آنها و دایره های محیطی شان (circumscribed circles) نشان می دهد (دایره های محیطی پیرامون یک مثلث ترسیم می شوند به نحویکه آن دایره از میان رأس های مثلث عبور کند). مراکز دایره محیطی، مرکز این دایره های محیطی می باشند.
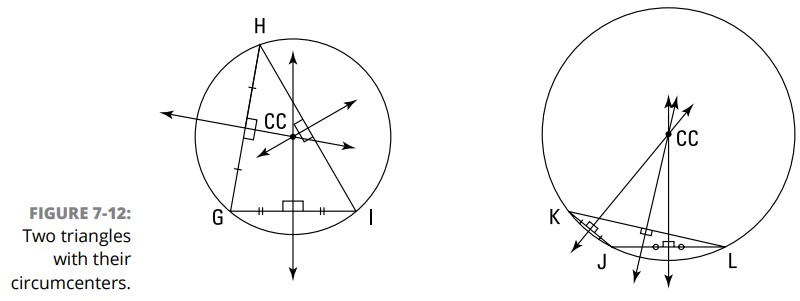
شما در شکل 12-7 می توانید ببینید که، برخلاف مراکز ثقل هندسی و مراکز دایره محاطی، یک مرکز دایره محیطی گاهی اوقات بیرون یک مثلث قرار می گیرد.
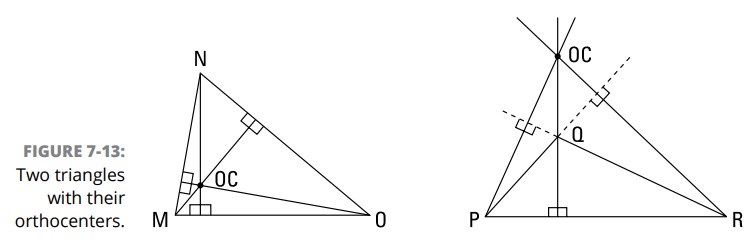
برای مشاهدۀ چند مرکز تعامد، شکل 13-7 را بررسی کنید. شما مرکز تعامد یک مثلث را در محل تقاطع ارتفاع های آن می یابید. برخلاف مرکز ثقل هندسی، مرکز دایره محاطی، و مرکز دایره محیطی ـــ که همگی آنها در یک نقطۀ محل تقاطع از یک مثلث قرار دارند (مرکز ثقل مثلث، نقطه ای که دارای مسافت یکسان از اضلاع مثلث است، و نقطه ای که دارای فاصلۀ یکسان از رأس های مثلث است)، ـــ مرکز تعامد یک مثلث در نقطه ای که دارای این نوع ویژگی های زیبا باشد، قرار نگرفته است.
اما به این چیز جالب توجه کنید: مجدداً به مثلث های موجود در شکل 13-7 نگاهی بیندازید. چهار نقطۀ برچسب گذاری شده در هر مثلث را در نظر بگیرید (سه رأس آن بعلاوۀ مرکز تعامد). اگر با سه نقطه از هر کدام از این چهار نقطه یک مثلث بسازید، نقطۀ چهارم مرکز تعامد آن مثلث می باشد. خیلی دلنشین بود، اینطور نیست؟
مراکز تعامد قوانینی مشابه قوانین مراکز دایره محیطی را دنبال می کنند (توجه داشته باشید که هم مراکز تعامد و هم مراکز دایره محیطی شامل خطهای عمود ـــ ارتفاع ها و نیمسازهای عمود می باشند).

مرکز ثقل هندسی (centroid)
قبل از اینکه مرکز ثقل هندسی را برای شما تعریف کنم، ابتدا نیاز به تعریف اصطلاح دیگری دربارۀ مثلث ها دارید: میانه (median).
میانه (median): میانۀ مثلث یک پاره خط است که از یکی از رأس های آن مثلث تا نقطۀ میانی (midpoint) ضلع مقابل آن می رود. هر مثلث سه میانه دارد. (شما از تعریف میانه در برخی از اثبات های مثلث استفاده خواهید کرد. فصل 9 را ببینید.)
مرکز ثقل هندسی (Centroid): سه میانۀ یک مثلث در مرکز ثقل هندسیِ آن، همدیگر را قطع می کنند. مرکز ثقل هندسی، نقطۀ تعادل، یا مرکز ثقل آن مثلث می باشد.
در هر میانه، فاصلۀ بین رأس تا مرکز ثقل هندسی دوبرابر فاصلۀ مرکز ثقل هندسی تا نقطۀ میانی می باشد. شکل 10-7 را ببینید.

\(X\) ، \(Y\) ، و \(Z\) نقاط میانی اضلاعِ \(\triangle{PQR}\) می باشند؛ \(\overline{RX}\) ، \(\overline{PY}\) ، و \(\overline{QZ}\) میانه ها می باشند؛ و این میانه ها در نقطۀ \(C\)، یعنی مرکز ثقل هندسی، یکدیگر را قطع می کنند. اگر خط کشتان را بیرون بکشید (یا فقط از انگشتانتان استفاده کنید)، می توانید بررسی کنید که مرکز ثقل هندسی در \({1\over3}\) میانه ها ، به عنوان مثال \(\overline{PY}\)، می باشد. به عبارت دیگر \(\overline{CY}\) برابر با \({1\over3}\) \(\overline{PY}\) می باشد (بنابراین \(\overline{CY}\) نصفِ \(\overline{CP}\) می باشد).
شما احتمالاً بخواهید تا واقعاً ببینید چگونه یک مثلث در مرکز ثقلش تعادل خواهد داشت. یک مثلث را در هر شکلی از یک تکه مقوای نسبتاً سفت و سخت برش دهید. با قدت نقطۀ میانی دو تا از ضلع های آن را بیابید، و سپس دو تا از میانه ها را به آن نقاط ترسیم کنید. جایی که این دو میانه همدیگر را قطع می کنند، مرکز ثقل هندسی این مثلث است (اگر بخواهید می توانید میانه سوم را نیز ترسیم کنیم، اما برای یافتن مرکز ثقل هندسی مثلث همان دو میانه کفایت خواهد کرد). حالا از چیزی با نوک مسطح و کوچک همچون یک مداد تراشیده نشده استفاد کنید، اگر مستقیماً مرکز ثقل را بر روی سطح صاف انتهای این مداد تراشیده نشده قرار دهید، مثلث تعادل خودش را حفظ خواهد کرد.
مرکز ثقل هندسیِ یک مثلث احتمالاً به عنوان یک نقطۀ خوب است که به شما محل تخمینی مرکز مثلث را بگوید. این مرکز ثقل هندسی قطعاً کاندیدای بهتری برای مرکزیت یک مثلث می باشد، بهتر از سه نقطه ای که در ادامه در موردشان بحث خواهم کرد.
یافتن سه مرکز دیگر برای یک مثلث
علاوه بر مرکز ثقل هندسی، هر مثلثی سه مرکز (centers) دیگر هم دارد که در محل تقاطع نیمخطها، خطها، و پاره خطهای مرتبط با این مثلث قرار گرفته اند.
-
مرکز دایره محاطی (Incenter): مرکز دایره محاطی جایی است که سه نیمساز (bisector) زاویه های یک مثلث یکدیگر را قطع می کنند (نیمساز یک زاویه یک نیمخط است که یک زاویه را به دو قسمت مساوی تقسیم می کند)؛ مرکز دایره محاطی، مرکز یک دایره است که درون آن مثلث محاط شده است (داخل مثلث ترسیم شده است).
-
مرکز دایره محیطی (Circumcenter): مرکز دایره محیطی جایی است که سه نیمساز عمود (perpendicular bisector) بر اضلاع یک مثلث، یکدیگر را قطع می کنند (یک نیمساز عمود یک خط است که با یک پاره خط زاویۀ \(90^{\circ}\) را شکل می دهد و آن پاره خط را به دو نیم تقسیم می کند)؛ مرکز دایره محیطی، مرکز یک دایره می باشد که پیرامون مثلث را محیط کرده است (در اطراف آن ترسیم شده است).
-
مرکز تعامد (Orthocenter): مرکز تعامد جایی است که سه ارتفاع (altitude) یک مثلث یکدیگر را قطع می کنند. (پیشتر در همین فصل در مورد ارتفاع مثلث بحث کردیم.)
مرکز دایره محاطی (Incenter)
شما مرکز دایره محاطی یک مثلث را در محل تقاطع سه نیمساز زوایای آن مثلث می یابید. این محل به مرکز دایره محاطی یک ویژگی جالب می دهد: مرکز دایره محاطی از هر سه ضلع یک مثلث در یک فاصلۀ برابر قرار دارد. هیچ نقطۀ دیگری این کیفیت را ندارد. مراکز دایره محاطی، همانند مراکز ثقل هندسی، همواره درون مثلث هایشان قرار دارند.
شکل 11-7 دو مثلث را با مراکز دایره محیطی شان و دایره های محاطی شان (inscribed circles)، نشان می دهد. (دایره های محاطی درون مثلث ها ترسیم می شوند، بنابراین این دایره ها به سختی اضلاع هر مثلث را لمس می کنند). مراکز دایره محاطی، مراکز این دایره های محاطی می باشند.

مرکز دایره محیطی (Circumcenter)
شما مرکز دایره محیطی یک مثلث را در محل تقاطع نیم ساز های عمود اضلاع آن می یابید. این محل به مرکز دایره محیطی یک ویژگی جالب می دهد: مرکز دایره محیطی از هر سه رأس یک مثلث فاصلۀ یکسانی دارد.
شکل 12-7 دو مثلث را همراه با مراکز دایره محیطی آنها و دایره های محیطی شان (circumscribed circles) نشان می دهد (دایره های محیطی پیرامون یک مثلث ترسیم می شوند به نحویکه آن دایره از میان رأس های مثلث عبور کند). مراکز دایره محیطی، مرکز این دایره های محیطی می باشند.

شما در شکل 12-7 می توانید ببینید که، برخلاف مراکز ثقل هندسی و مراکز دایره محاطی، یک مرکز دایره محیطی گاهی اوقات بیرون یک مثلث قرار می گیرد.
-
مرکز دایره محیطی، داخل تمامی مثلث های حاده الزوایه (acute triangles) قرار دارد.
-
مرکز دایره محیطی، بیرون تمامی مثلث های منفرجه الزوایه (obtuse triangles) قرار دارد.
-
مرکز دایره محیطی، در تمامی مثلث های قائم الزاوایه (right triangles) در نقطۀ میانی وتر قرار دارد.
مرکز تعامد (Orthocenter)
برای مشاهدۀ چند مرکز تعامد، شکل 13-7 را بررسی کنید. شما مرکز تعامد یک مثلث را در محل تقاطع ارتفاع های آن می یابید. برخلاف مرکز ثقل هندسی، مرکز دایره محاطی، و مرکز دایره محیطی ـــ که همگی آنها در یک نقطۀ محل تقاطع از یک مثلث قرار دارند (مرکز ثقل مثلث، نقطه ای که دارای مسافت یکسان از اضلاع مثلث است، و نقطه ای که دارای فاصلۀ یکسان از رأس های مثلث است)، ـــ مرکز تعامد یک مثلث در نقطه ای که دارای این نوع ویژگی های زیبا باشد، قرار نگرفته است.
اما به این چیز جالب توجه کنید: مجدداً به مثلث های موجود در شکل 13-7 نگاهی بیندازید. چهار نقطۀ برچسب گذاری شده در هر مثلث را در نظر بگیرید (سه رأس آن بعلاوۀ مرکز تعامد). اگر با سه نقطه از هر کدام از این چهار نقطه یک مثلث بسازید، نقطۀ چهارم مرکز تعامد آن مثلث می باشد. خیلی دلنشین بود، اینطور نیست؟

مراکز تعامد قوانینی مشابه قوانین مراکز دایره محیطی را دنبال می کنند (توجه داشته باشید که هم مراکز تعامد و هم مراکز دایره محیطی شامل خطهای عمود ـــ ارتفاع ها و نیمسازهای عمود می باشند).
-
مرکز تعامد، داخل تمامی مثلث های حاده الزوایه (acute triangles) قرار دارد.
-
مرکز تعامد، بیرون تمامی مثلث های منفرجه الزوایه (obtuse triangles) قرار دارد.
-
مرکز تعامد، در تمامی مثلث های قائم الزاوایه (right triangles) در رأس زاویه قائمه قرار دارد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: