خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
قضیۀ مثلث متساوی الساقین

بخش های پیشین در این فصل شامل جفت هایی از مثلث های همنهشت بودند. در اینجا، شما با دو قضیه آشنا می شوید که یک مثلث متساوی الساقین (isosceles triangle) را در بر می گیرند. اگرچه، شما اغلب در اثباتهای مربوط به همنهشت بودن دو مثلث به این قضایا نیاز دارید، اما خود این قضایا تنها به یک مثلث مربوط می شوند.

در اینجا یک اثبات داریم. سعی کنید از یک استراتژی بازی برای پیشبرد گام به گام استفاده کنید و قبل از اینکه اثبات من را بخوانید، اثبات خودتان را بنویسید و در پایان با پاسخ صحیح مقایسه کنید.
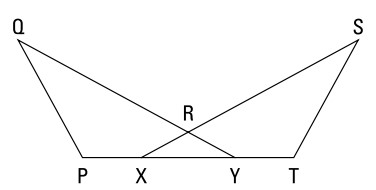
داده ها:
\(\angle{P} \cong \angle{T}\)
\(\overline{PX} \cong \overline{TY}\)
\(\overline{RX} \cong \overline{RY}\)
اثبات کنید:
\(\angle{Q} \cong \angle{S}\)
در اینجا یک استراتژی بازی داریم:
اثبات رسمی را در اینجا بررسی کنید:


دو قضیۀ زیر مبتنی بر یک ایده ساده در مورد مثلث های متساوی الساقین می باشند که در هر دو جهت به درستی کار می کنند:
-
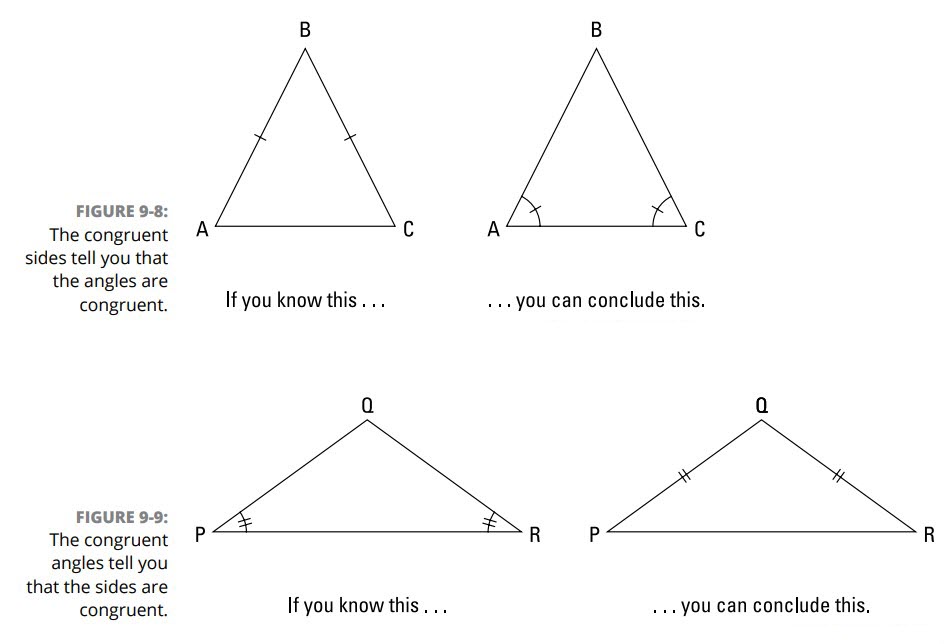
اگر اضلاع، سپس زوایا: اگر دو ضلع از یک مثلث با یکدیگر همنهشت باشند، سپس زوایای روبروی آن اضلاع با یکدیگر همنشهت می باشند. شکل 8-9 چگونگی کار کرد این مسأله را نشان می دهد.
-
اگر زاویه ها، سپس اضلاع: اگر دو زاویه از یک مثلث با یکدیگر همنهشت باشند، سپس اضلاع مقابل آن زاویه ها با یکدیگر همنهشت می باشند. شکل 9-9 را ببینید.

نکته: به مثلث های متساوی الساقین بنگرید. قضیۀ دو زاویه-ضلع (two angle-side theorems) برای حل کردن بسیاری از اثبات ها حیاتی می باشد، بنابراین هنگامی که شروع به حل کردن یک اثبات می کنید، به شکل هندسی نگاه کنید و تمامی مثلث هایی را که به نظر متساوی الساقین می آیند، شناسایی کنید. سپس یادتان باشد که شما ممکن است مجبور شوید یکی از دو قضایای پبشین را برای یک یا چند مثلث متساوی الساقین بکار بگیرید. اگر بتوانید مثلث های متساوی الساقین را شناسایی کنید (که نباید کار سختی باشد)، استفاده از این قضایا بسیار ساده می باشد. اما اگر در شناسایی آنها دچار اشتباه شوید، ممکن است انجام اثبات غیرممکن شود. و توجه داشته باشید که در اینجا هدف شما اینست که یک مثلث متساوی الساقین واحد را شناسایی کنید، زیرا برخلاف SSS، SAS، و ASA ، قضیۀ مثلث متساوی الساقین شامل جفت هایی از مثلث ها نمی شود.
در اینجا یک اثبات داریم. سعی کنید از یک استراتژی بازی برای پیشبرد گام به گام استفاده کنید و قبل از اینکه اثبات من را بخوانید، اثبات خودتان را بنویسید و در پایان با پاسخ صحیح مقایسه کنید.

داده ها:
\(\angle{P} \cong \angle{T}\)
\(\overline{PX} \cong \overline{TY}\)
\(\overline{RX} \cong \overline{RY}\)
اثبات کنید:
\(\angle{Q} \cong \angle{S}\)
در اینجا یک استراتژی بازی داریم:
-
شکل هندسیِ اثبات را برای یافتن مثلث های متساوی الساقین و جفت مثلث های همنهشت بررسی کنید.
این شکل هندسی دارای یک مثلث متساوی الساقین می باشد، که یک راهنمای بزرگ در مورد اینست که شما در حال استفاده از یکی از قضایای مثلث متساوی الساقین می باشید. شما همچنین یک جفت مثلث دارید که به نظر همنهشت می رسند (مثلث هایی که همپوشانی دارند)، که خود این هم راهنمای بزرگ دیگری می باشد که شما باید نشان دهید آنها همنهشت می باشند.
-
در مورد چگونگی اتمامِ این اثبات با قضیۀ همنهشتی مثلث و CPCTC فکر کنید.
اضلاع یک مثلث متساوی الساقین به شما داده شده اند، بنابراین این به شما زوایای همنهشت را می دهد. همچنین در داده های مسأله دارید \(\angle{P} \cong \angle{T}\) ، بنابراین اکنون جفت دومی از زوایای همنهشت را دارید. اگر بتوانید به \(\overline{PY} \cong \overline{TX}\) برسید، ASA را خواهید داشت. و شما می توانید با افزودن \(\overline{XY}\) به دو پاره خط همنهشت داده شده، یعنی \(\overline{PX}\) و \(\overline{TY}\) ، به آن برسید. اکنون می توانید با CPCTC اثبات را تمام کنید.
اثبات رسمی را در اینجا بررسی کنید:

ترجمۀ شکل:
-
\(\overline{RX} \cong \overline{RY}\)
داده ها.
-
\(\angle{RYX} \cong \angle{RXY}\)
اگر دو ضلع یک مثلث همنهشت باشند، سپس زوایای مقابل آن اضلاع با یکدیگر همنشهت هستند.
-
\(\overline{PX} \cong \overline{TY}\)
داده ها.
-
\(\overline{PY} \cong \overline{TX}\)
اگر یک پاره خط به دو پاره خط همنشهت اضافه گردد، سپس مجموع آنها همنهشت می باشند.
-
\(\angle{P} \cong \angle{T}\)
داده ها.
-
\(\triangle{PQY} \cong \triangle{TSX}\)
اصل ASA (گزاره های 2،4،5).
-
\(\angle{Q} \cong \angle{S}\)
CPCTC
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: