خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ویژگیهای چهارضلعی ها
ویژگیهای (properties) چهارضلعی ها به سادگی چیزهایی هستند که در مورد آنها صحیح می باشند. ویژگیهای یک چهارضلعی خاص به موارد زیر مربوط می شود:

در اینجا مجموعاً در حدود 30 ویژگی چهارضلعی ها را ارائه می کنم، که به نظر می رسد برای حفظ کردن زیاد باشد. نگران نباشید. شما نیازی ندارید تا صرفاً بر حفظ کردن تکیه کنید. در اینجا یک نکتۀ عالی داریم که یادگیری این ویژگیها را به سادگی یک بشکن زدن می کند.
من احساس می کنم، شما می توانید حدس بزنید چه چیزهایی در این بخش گفته خواهند شد. چیزی را که می خواستید بدست آوردید ـــ ویژگیهای متوازی الاضلاع.
اگر صرفاً به یک متوازی الاضلاع بنگرید، چیزهای که صحیح به نظر می رسند (یعنی، چیزهای موجود در این لیست) واقعاً صحیح هستند و از این رو از ویژگیها می باشند، و چیزهایی که به نظر صحیح نمی آیند، واقعاً نادرست هستند و از ویژگیها نمی باشند.
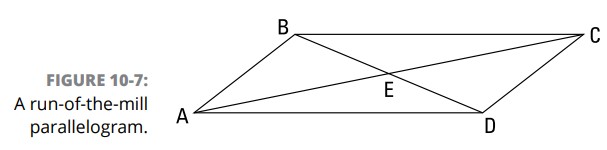
تصور کنید نمی توانید ویژگیهای یک متوازی الاضلاع را به یاد بیاورید. شما می توانید صرفاً یک متوازی الاضلاع (مانند شکل 7-10) ترسیم کنید و تمامی چیزهایی را که ممکن است از ویژگیها باشند، بررسی کنید.
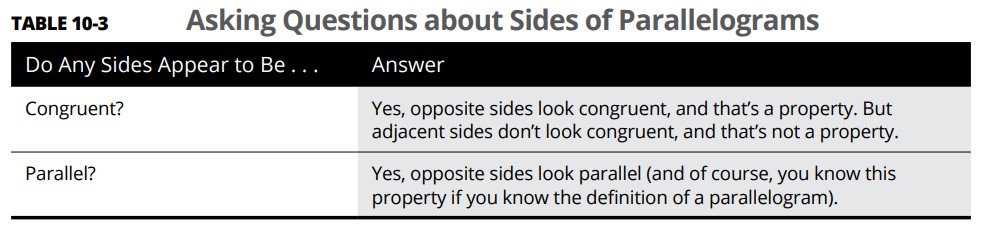
جدول 3-10 مرتبط با سوالاتی در مورد اضلاع یک متوازی الاضلاع می باشد (شکل 7-10 را ببینید).
ترجمۀ جدول:
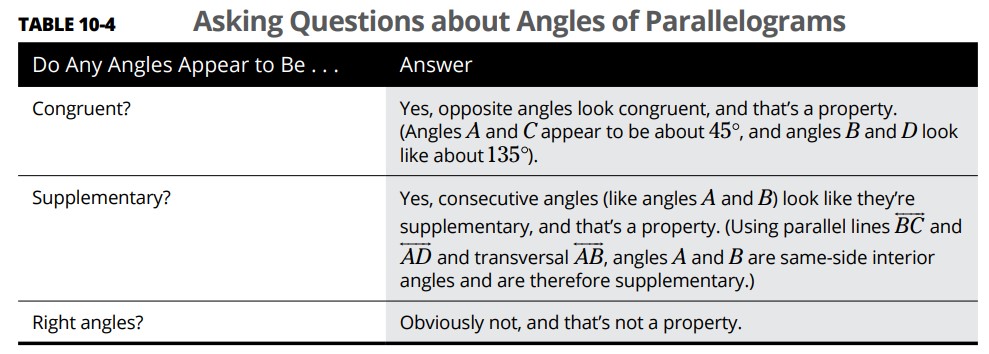
جدول 4-10 زوایای یک متوازی الاضلاع را مورد بررسی قرار می دهد (شکل 7-10 را دوباره ببینید).
ترجمۀ جدول:
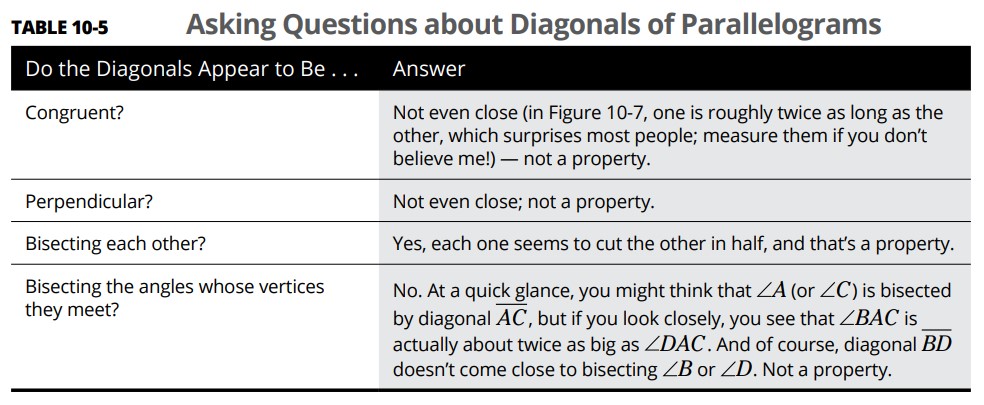
جدول 5-10 به گزاره هایی دربارۀ قطرهای یک متوازی الاضلاع اشاره می کند (شکل 7-10 را ببینید).
ترجمۀ شکل:
روش ترسیم چهارضلعی و سوالات موجود در سه جدولی که دیدید، یک نکته کلی مهم در مورد ریاضیات را به خاطر من می آورد.
و اکنون یک اثبات متوازی الاضلاع داریم:
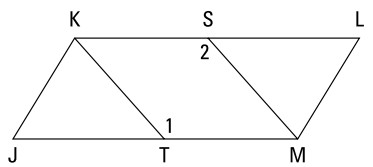
داده ها:
\(JKLM\) یک متوازی الاضلاع می باشد
\(T\) نقطۀ میانی \(\overline{JM}\) می باشد
\(S\) نقطۀ میانی \(\overline{KL}\) می باشد
اثبات کنید:
\(\angle{1} \cong \angle{2}\)
فرآیند فکری شما ممکن است چیزی شبیه این باشد:
در اینجا اثبات رسمی را داریم:

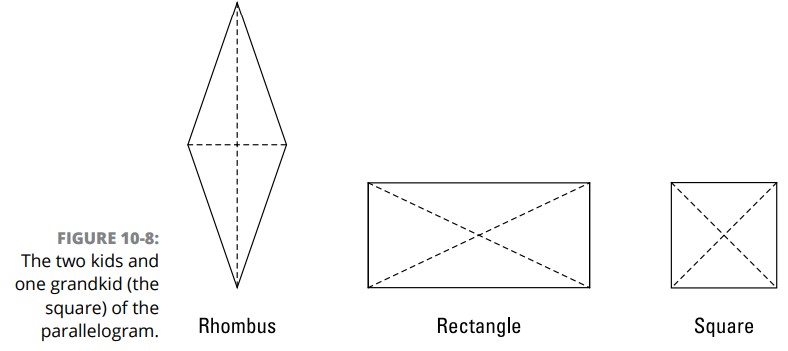
شکل 8-10 سه متوازی الاضلاع خاص را به شما نشان می دهد، دلیل این نامگذاری همانطور که ریاضیدانان می گویند اینست که موارد خاصی از متوازی الاضلاع می باشند. (علاوه بر این، مربع یک مورد یا نوع خاص از هم مستطیل و هم لوزی می باشد.) سلسله مراتب سه سطحی که شما در درخت خانوادۀ متوازی الاضلاع (شکل 3-10) در متوازی الاضلاع \(\leftarrow\) مستطیل \(\leftarrow\) مربع و یا در متوازی الاضلاع \(\leftarrow\) لوزی \(\leftarrow\) مربع می بینید، درست مانند پستاندار \(\leftarrow\) سگ \(\leftarrow\) نژاد دالمیشن می باشد. یک سگ نوع خاصی از پستانداران می باشد، و یک دالمیشن نوع خاصی (نژاد خاصی) از سگ می باشد.
قبل از اینکه ویژگیهایی را که در ادامه می آید بخوانید، سعی کنید خودتان آنها را کشف کنید. با استفاده از شکلهای موجود در تصویر 8-10 ، لیست ویژگیهای محتمل را بررسی کنید. از خودتان بپرسید آیا چیزهایی که در این لوزی، مستطیل، و مربع به نظر صحیح می رسند، به واقع صحیح می باشند. (توجه داشته باشید که هم لوزی و هم مستطیل ترسیم شده در شکل 8-10 تا حد امکان عمومی ترسیم شده اند؛ به عبارت دیگر، هیچکدام از آنها شبیه یک مربع نیستند. همچنین، توجه داشته باشید که این لوزی به جای اینکه مانند یک متوازی الاضلاع بر روی یکی از اضلاعش باشد، به صورت عمودی است؛ این یک روش ساده تر و بهتر برای ترسیم لوزی می باشد، زیرا به آسانی می توانید تقارن آن و این واقعیت که قطرهای آن متعامد می باشند را ببینید.)
اکنون سعی کنید تا با چندین مسأله درگیر شوید: مستطیل زیر به شما داده شده است، اندازۀ \(\angle{1}\) و \(\angle{2}\) را بیابید:
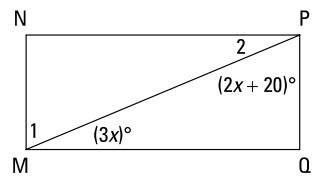
این هم پاسخ: \(MNPQ\) یک مستطیل است، بنابراین \(\angle{Q}=90^{\circ}\) . سپس، از آنجایی که در یک مثلث \(180^{\circ}\) وجود دارد، شما می توانید بگویید:
$$
90^{\circ} +(3x)^{\circ}+(2x+20)^{\circ}=180^{\circ}\\
3x+2x+20=90\\
5x=70\\
x=14
$$
اکنون \(14\) را در تمامی \(x\) جایگذاری کنید. زاویۀ \(QMP\) ، یعنی \((3x)^{\circ}\) ، برابر با \(3 \cdot 14\) یا \(42^{\circ}\) می شود، و از آنجا که شما یک مستطیل دارید، \(\angle{1}\) متمم \(\angle{QMP}\) خواهد بود و بنابراین برابر با \(90^{\circ}-42^{\circ}\) یا \(48^{\circ}\) می باشد. زاویۀ \(QMP\) ، یعنی \((2x+20)^{\circ}\) ، برابر با \(2 \cdot 14 +20\) یا \(48^{\circ}\) خواهد بود، و \(\angle{2}\) ، یعنی متمم آن، می شود \(42^{\circ}\).
اکنون محیط لوزی \(RHOM\) را بیابید.

پاسخ این مسأله: تمامی اضلاع یک لوزی همنهشت می باشند، بنابراین \(HO\) برابر با \(x+2\) خواهد بود. و از آنجا که قطرهای یک لوزی متعامد می باشند، \(\triangle{HBO}\) یک مثلث قائم الزاویه می باشد. شما می توانید این مسأله را با قضیۀ فیثاغورث به پایان برسانید:
$$
a^2+b^2=c^2\\
(HB)^2+(BO)^2=(HO)^2\\
x^2+(x+1)^2=(x+2)^2\\
x^2+x^2+2x+1=x^2+4x+4\\
x^2-2x-3=0\\
(x-3)(x+1)=0 \\
x-3=0 \text { or } x+1=0 \\
x=3 \text { or } x=-1
$$
شما می توانید \(x=-1\) را نادیده بگیرید، زیرا منجر می شود تا یکی از ساق های \(\triangle{HBO}\) برابر با \(-1\) و ساق دیگر برابر با \(0\) گردد. بنابراین \(x\) برابر با \(3\) می باشد، که منجر می شود تا \(\overline{HR}\) دارای طول \(5\) باشد. از آنجا که لوزی ها دارای چهار ضلع همنهشت می باشند، محیط \(RHOM\) برابر با \(4 \cdot 5\) یا \(20\) واحد می باشد.
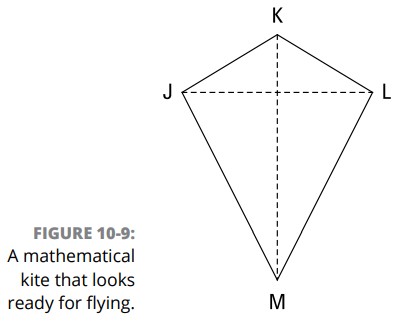
کایت (شبه لوزی) موجود در شکل 9-10 را بررسی کنید و سعی کنید تا قبل از خواندن لیستی که در ادامه آمده است، ویژگیهای آن را کشف کنید.
سه ویژگی آخر، خواص نیمه (half properties) در کایت نامیده می شوند.
یک نوشیدنی انرژی زا بخورید و برای اثبات دیگری آماده باشید. با توجه به محدودیت جا، قصد دارم تا این بار استراتژی بازی را نادیده بگیرم. در مورد استراتژی بازی بعد از این باید به خودتان متکی باشید.
داده ها:
\(RSTV\) یک کایت با \(\overline{RS} \cong \overline{TS}\) می باشد
\(\overline{WV} \cong \overline{UV}\)
اثبات کنید:
\(\overline{WS} \cong \overline{US}\)

شاید سختترین ویژگی برای تشخیص دادن در هر دو شکل هندسی موردی است که دربارۀ زوایای مکمل می باشد. به دلیل وجود اضلاع موازی، زوایای متوالی، زوایای هم سمت داخلی می باشند و از این رو مکمل یکدیگرند. (راستی، تمامی چهارضلعی ها به جز کایت، شامل زوایای متوالی مکمل می باشند.)
در اینجا یک اثبات ذوزنقۀ متساوی الساقین برای شما داریم. در مورد استراتژی بازی دوباره به شما اعتماد می کنم تا خودتان از عهده اش برآیید.
داده ها:
\(ZOID\) یک ذوزنقۀ متساوی الساقین با قاعده های \(\overline{OI}\) و \(\overline{ZD}\) می باشد
اثبات کنید:
\(\overline{TO} \cong \overline{TI}\)


-
اضلاع: آیا همنهشت هستند؟ آیا موازی هستند؟
-
زوایا: آیا همنهشت هستند؟ آیا مکمل هستند؟ آیا قائمه هستند؟
-
قطرها: آیا همنهشت هستند؟ آیا متعامد هستند؟ آیا یکدیگر را تنصیف می کنند؟ آیا زاویایی را که به راس های آنها برخورد می کند، تنصیف می کنند؟
در اینجا مجموعاً در حدود 30 ویژگی چهارضلعی ها را ارائه می کنم، که به نظر می رسد برای حفظ کردن زیاد باشد. نگران نباشید. شما نیازی ندارید تا صرفاً بر حفظ کردن تکیه کنید. در اینجا یک نکتۀ عالی داریم که یادگیری این ویژگیها را به سادگی یک بشکن زدن می کند.
اگر نتوانید به یاد آورید که آیا چیزی یک ویژگی از یک چندضلعی خاص می باشد، کافیست آن چندضلعی را در مسأله ترسیم کنید. اگر چیزها به نظر صحیح برسند، احتمالاً یک ویژگی باشند؛ اگر صحیح به نظر نرسند، یک ویژگی نمی باشند. (این روش تقریباً بدون خطا است، اما اندکی غیر از اصول آموزگاران ریاضی می باشد ، بنابراین هیچ جا آن را از من نقل قول نکنید، ممکن است پلیس ریاضی برای من دردسر درست کند!)
ویژگیهای متوازی الاضلاع (parallelogram)
من احساس می کنم، شما می توانید حدس بزنید چه چیزهایی در این بخش گفته خواهند شد. چیزی را که می خواستید بدست آوردید ـــ ویژگیهای متوازی الاضلاع.
متوازی الاضلاع دارای ویژگیهای زیر می باشد:
-
اضلاع روبروی هم بنا به تعریف موازی می باشند.
-
اضلاع رو به روی هم همنهشت می باشند.
-
زوایای روبروی هم همنهشت می باشند.
-
زوایای متوالی مکمل یکدیگر می باشند.
-
قطرها یکدیگر را تنصیف می کنند.
اگر صرفاً به یک متوازی الاضلاع بنگرید، چیزهای که صحیح به نظر می رسند (یعنی، چیزهای موجود در این لیست) واقعاً صحیح هستند و از این رو از ویژگیها می باشند، و چیزهایی که به نظر صحیح نمی آیند، واقعاً نادرست هستند و از ویژگیها نمی باشند.
اگر برای کمک به فهمیدنِ ویژگیهای یک چهارضلعی تصویری را ترسیم می کنید، تصویر مورد نظر را تا حد امکان عمومی بکشید. به عنوان مثال، موقع ترسیم یک متوازی الاضلاع، مطمئن شوید که تقریباً شبیه لوزی نشده باشد (با چهار ضلع که تقریباً همنهشتند) یا شبیه مربع نشود (با چهار زاویه که قائمه به نظر می رسند). اگر طرح متوازی الاضلاع شما، فرض کنید شبیه مربع شود، چیزهایی را خواهید دید که برای تمامی مربع ها صحیح به نظر می رسند اما در مورد همه متوازی الاضلاع ها صحیح نمی باشند (مانند قطرهای همنهشت)، و ممکن است شما به اشتباه نتیجه گیری کنید که یک ویژگی از متوازی الاضلاع می باشد.
تصور کنید نمی توانید ویژگیهای یک متوازی الاضلاع را به یاد بیاورید. شما می توانید صرفاً یک متوازی الاضلاع (مانند شکل 7-10) ترسیم کنید و تمامی چیزهایی را که ممکن است از ویژگیها باشند، بررسی کنید.

جدول 3-10 مرتبط با سوالاتی در مورد اضلاع یک متوازی الاضلاع می باشد (شکل 7-10 را ببینید).

ترجمۀ جدول:
|
سوال |
پاسخ |
|---|---|
|
آیا هیچ کدام از اضلاع همنهشت به نظر می رسند؟ |
بله، اضلاع روبروی یکدیگر همنهشت به نظر می رسند، و این یک ویژگی می باشد. اما اضلاع مجاور یکدیگر همنهشت به نظر نمی رسند، و این یک ویژگی نمی باشد. |
|
آیا هیچ کدام از اضلاع موازی به نظر می رسند؟ |
بله، اضلاع روبروی یکدیگر موازی به نظر می رسند (و البته اگر شما تعریف متوازی الاضلاع را بدانید، قطعاً این ویژگی را هم می دانید). |
جدول 4-10 زوایای یک متوازی الاضلاع را مورد بررسی قرار می دهد (شکل 7-10 را دوباره ببینید).

ترجمۀ جدول:
|
سوال |
پاسخ |
|---|---|
|
آیا هیچکدام از زوایا همنهشت به نظر می رسند؟ |
بله، زوایای روبروی یکدیگر همنهشت به نظر می رسند، و این یک ویژگی می باشد. (زوایای \(A\) و \(C\) به نظر \(45^{\circ}\) می رسند، و زوایای \(B\) و \(D\) در حدود \(135^{\circ}\) به نظر می آیند). |
|
آیا هیچدام از زوایا مکمل به نظر می رسند؟ |
بله، زوایای متوالی (مانند زاویه های \(A\) و \(B\)) به نظر مکمل یکدیگر می باشند، و این یک ویژگی می باشد. (با استفاده از خطوط موازی \(\overleftrightarrow{BC}\) و \(\overleftrightarrow{AD}\) و خط متقاطع \(\overleftrightarrow{AB}\)، زوایای \(A\) و \(B\) زوایای هم سمت داخلی می باشند و از این رو مکمل یکدیگرند.) |
|
آیا هیچکدام از زوایا قائمه به نظر می رسند؟ |
قطعاً خیر، و این یک ویژگی نمی باشد. |
جدول 5-10 به گزاره هایی دربارۀ قطرهای یک متوازی الاضلاع اشاره می کند (شکل 7-10 را ببینید).

ترجمۀ شکل:
|
سوال |
جواب |
|---|---|
|
آیا قطرها همنهشت به نظر می رسند؟ |
خیر ابداً (در شکل 7-10، یکی از قطرها تقریباً دو برابر دیگر به نظر می آید، که این موضوع بیشتر افراد را سورپرایز می کند؛ اگر حرف من را باور ندارید قطرها را اندازه گیری کنید!) ـــ یک ویژگی نمی باشد. |
|
آیا قطرها متعامد به نظر می رسند؟ |
خیر، به هیچ وجه؛ یک ویژگی نمی باشد. |
|
آیا به نظر می رسد، قطرها همدیگر را تنصیف کرده باشند؟ |
بله، به نظر می رسد هر کدامشان دیگری را از وسط بریده باشد، و این یک ویژگی می باشد. |
|
آیا به نظر می رسد، قطرها زوایایی را که با رأس آنها برخورد داشته اند را تنصیف کرده باشند؟ |
خیر. در یک نگاه سریع، ممکن است فکر کنید که \(\angle{A}\) (یا \(\angle{C}\)) توسط قطر \(\overline{AC}\) تنصیف شده باشد، اما اگر با دقت بیشتری نگاه کنید، خواهید دید که \(\angle{BAC}\) در واقع در حدود دوبرابر بزرگتر از \(\angle{DAC}\) می باشد. و قطعاً، به نظر نمی رسد قطر \(\overline{BD}\) زوایای \(\angle{B}\) یا \(\angle{D}\) را تنصیف کرده باشد. یک ویژگی نیست. |
به طرحتان با دقت نگاه کنید. هنگامی که یک متوازی الاضلاع مانند این را به دانش آموزانم نشان می دهم و از آنها می پرسم که آیا قطرها همنهشت به نظر می رسند، آنها اغلب می گویند بله، در صورتیکه اگر کمی دقت کنید متوجه خواهید شد یکی از آنها دقیقاً دوبرابر قطر دیگر است! بنابراین هنگامی که از خودتان سوال می کنید آیا یک ویژگی بالقوه صحیح به نظر می آید، فقط نگاه سریعی به شکل نیندازید و اجازه ندهید چشمانتان شما را فریب بدهند. به زوایا و پاره خطهای شکل با دقت بیشتری نگاه کنید.
روش ترسیم چهارضلعی و سوالات موجود در سه جدولی که دیدید، یک نکته کلی مهم در مورد ریاضیات را به خاطر من می آورد.
هرگاه که ممکن باشد، قواعد، فرمول ها، مفاهیم، و به همین ترتیب را با بررسی اینکه چرا آنها صحیح می باشند یا چرا با معنا به نظر می رسند، در حافظۀ خودتان تقویت کنید. این کار نه تنها حفظ کردن آن مفهوم را ساده تر می سازد، همچنین به شما کمک می کند ارتباط آن را با سایر مفاهیم درک کنید، و منجر می شود تا درک عمیقتری از ریاضیات پیدا کنید.
و اکنون یک اثبات متوازی الاضلاع داریم:

داده ها:
\(JKLM\) یک متوازی الاضلاع می باشد
\(T\) نقطۀ میانی \(\overline{JM}\) می باشد
\(S\) نقطۀ میانی \(\overline{KL}\) می باشد
اثبات کنید:
\(\angle{1} \cong \angle{2}\)
از ویژگیهای چهارضلعی در اثباتهای چهارضلعی استفاده کنید. اگر یکی از داده ها در یک اثبات این باشد که یک شکل یک چهارضلعی خاص می باشد، شما می توانید مطمئن باشید که نیاز دارید تا از یک یا چند تا از ویژگیهای آن چهارضلعی در اثبات استفاده کنید ـــ معمولاً برای نمایش همنهشتی مثلث ها.
فرآیند فکری شما ممکن است چیزی شبیه این باشد:
-
به مثلث های همنهشت توجه کنید.
اگر بتوانید اثبات کنید مثلث ها همنهشت هستند، می توانید با CPCTC به \(\angle{JTK} \cong \angle{LSM}\) برسید و سپس با مکمل های زوایای همنهشت به \(\angle{1} \cong \angle{2}\) برسید.
-
همنهشت بودن مثلث ها را اثبات کنید.
آیا می توانید از برخی از ویژگیهای متوازی الاضلاع استفاده کنید؟ قطعاً: اضلاع روبرو همنهشت می باشند به شما \(\overline{JK} \cong \overline{LM}\) را نتیجه می دهد، و زوایای روبرو همنشهت می باشند به شما \(\angle{J} \cong \angle{L}\) را می دهد. دو جفت همنهشت بدست آمده اند و یکی مانده است. دو نقطۀ میانی در داده ها سرنخی از این می باشد که شما نیاز به استفاده از تقسیمات مشابه دارید (فصل 5 را ببینید). تمام شد ـــ شما اضلاع همنهشت \(\overline{JM}\) و \(\overline{KL}\) را به دو نیم می کنید تا به شما \(\overline{JT} \cong \overline{LS}\) را نتیجه بدهد، که همنهشتی دو مثلث با SAS را به شما نتیجه می دهد.
در اینجا اثبات رسمی را داریم:

ترجمۀ شکل:
-
\(JKLM\) یک متوازی الاضلاع می باشد
داده.
-
\(\overline{JK} \cong \overline{LM}\)
اضلاع روبرو در متوازی الاضلاع همنهشت می باشند.
-
\(\angle{J} \cong \angle{L}\)
زوایای روبرو در متوازی الاضلاع همنهشت می باشند.
-
\(\overline{JM} \cong \overline{KL}\)
اضلاع روبرو در متوازی الاضلاع همنهشت می باشند.
-
\(T\) نقطۀ میانی \(\overline{JM}\) می باشد
\(S\) نقطۀ میانی پاره خط \(\overline{KL}\) می باشد
داده.
-
\(\overline{JT} \cong \overline{LS}\)
تقسیمات مشابه.
-
\(\triangle{JTK} \cong \triangle{LSM}\)
اصل SAS (گزاره های 2،3،6).
-
\(\angle{JTK} \cong \angle{LSM}\)
CPCTC
-
\(\angle{1} \cong \angle{2}\)
مکمل های زوایای همنهشت، همنهشت می باشند.
ویژگیهای سه متوازی الاضلاع خاص
شکل 8-10 سه متوازی الاضلاع خاص را به شما نشان می دهد، دلیل این نامگذاری همانطور که ریاضیدانان می گویند اینست که موارد خاصی از متوازی الاضلاع می باشند. (علاوه بر این، مربع یک مورد یا نوع خاص از هم مستطیل و هم لوزی می باشد.) سلسله مراتب سه سطحی که شما در درخت خانوادۀ متوازی الاضلاع (شکل 3-10) در متوازی الاضلاع \(\leftarrow\) مستطیل \(\leftarrow\) مربع و یا در متوازی الاضلاع \(\leftarrow\) لوزی \(\leftarrow\) مربع می بینید، درست مانند پستاندار \(\leftarrow\) سگ \(\leftarrow\) نژاد دالمیشن می باشد. یک سگ نوع خاصی از پستانداران می باشد، و یک دالمیشن نوع خاصی (نژاد خاصی) از سگ می باشد.
قبل از اینکه ویژگیهایی را که در ادامه می آید بخوانید، سعی کنید خودتان آنها را کشف کنید. با استفاده از شکلهای موجود در تصویر 8-10 ، لیست ویژگیهای محتمل را بررسی کنید. از خودتان بپرسید آیا چیزهایی که در این لوزی، مستطیل، و مربع به نظر صحیح می رسند، به واقع صحیح می باشند. (توجه داشته باشید که هم لوزی و هم مستطیل ترسیم شده در شکل 8-10 تا حد امکان عمومی ترسیم شده اند؛ به عبارت دیگر، هیچکدام از آنها شبیه یک مربع نیستند. همچنین، توجه داشته باشید که این لوزی به جای اینکه مانند یک متوازی الاضلاع بر روی یکی از اضلاعش باشد، به صورت عمودی است؛ این یک روش ساده تر و بهتر برای ترسیم لوزی می باشد، زیرا به آسانی می توانید تقارن آن و این واقعیت که قطرهای آن متعامد می باشند را ببینید.)

در اینجا ویژگیهای لوزی، مستطیل، و مربع را داریم. توجه داشته باشید که از آنجایی که هر سۀ این چهارضلعی ها متوازی الاضلاع می باشند، ویژگیهای آنها شامل ویژگیهای متوازی الاضلاع نیز می باشد..
-
لوزی دارای ویژگیهای زیر می باشد:
-
شامل تمامی ویژگیهای یک متوازی الاضلاع می شود (مواردی که در اینجا حائز اهمیت می باشند عبارت از اینها می باشند: اضلاع موازی، زوایای موازی همنهشت می باشند،و زوایای متوالی مکمل هستند).
-
تمامی اضلاع بنا به تعریف همنهشت می باشند.
-
قطرها زوایا را تنصیف می کنند.
-
قطرها عمود منصف یکدیگر می باشند.
-
شامل تمامی ویژگیهای یک متوازی الاضلاع می شود (مواردی که در اینجا حائز اهمیت می باشند عبارت از اینها می باشند: اضلاع موازی، زوایای موازی همنهشت می باشند،و زوایای متوالی مکمل هستند).
-
مستطیل دارای ویژگیهای زیر می باشد:
-
تمامی ویژگیهای یک متوازی الاضلاع را شامل می شود (مواردی که در اینجا مهمند عبارتند از: اضلاع موازی، اضلاع روبرو همنشهت می باشند، و قطرها یکدیگر را تنصیف می کنند).
-
تمامی زوایا بنا به تعریف قائمه می باشند.
-
قطرها همنهشت می باشند.
-
تمامی ویژگیهای یک متوازی الاضلاع را شامل می شود (مواردی که در اینجا مهمند عبارتند از: اضلاع موازی، اضلاع روبرو همنشهت می باشند، و قطرها یکدیگر را تنصیف می کنند).
-
مربع دارای ویژگیهای زیر می باشد:
-
تمامی ویژگیهای یک لوزی را شامل می گردد (موارد حائز اهمیت در اینجا عبارتند از: اضلاع موازی، قطرها عمود منصف یکدیگر می باشند، و قطرها یکدیگر را تنصیف می کنند).
-
تمامی ویژگیهای یک مستطیل را شامل می گردد (تنها مورد حائز اهمیت در اینجا اینست که قطرها همنهشت می باشند).
-
تمامی اضلاع بنا به تعریف همنهشت می باشند.
-
تمامی زوایا بنا به تعریف قائمه می باشند.
-
تمامی ویژگیهای یک لوزی را شامل می گردد (موارد حائز اهمیت در اینجا عبارتند از: اضلاع موازی، قطرها عمود منصف یکدیگر می باشند، و قطرها یکدیگر را تنصیف می کنند).
اکنون سعی کنید تا با چندین مسأله درگیر شوید: مستطیل زیر به شما داده شده است، اندازۀ \(\angle{1}\) و \(\angle{2}\) را بیابید:

این هم پاسخ: \(MNPQ\) یک مستطیل است، بنابراین \(\angle{Q}=90^{\circ}\) . سپس، از آنجایی که در یک مثلث \(180^{\circ}\) وجود دارد، شما می توانید بگویید:
$$
90^{\circ} +(3x)^{\circ}+(2x+20)^{\circ}=180^{\circ}\\
3x+2x+20=90\\
5x=70\\
x=14
$$
اکنون \(14\) را در تمامی \(x\) جایگذاری کنید. زاویۀ \(QMP\) ، یعنی \((3x)^{\circ}\) ، برابر با \(3 \cdot 14\) یا \(42^{\circ}\) می شود، و از آنجا که شما یک مستطیل دارید، \(\angle{1}\) متمم \(\angle{QMP}\) خواهد بود و بنابراین برابر با \(90^{\circ}-42^{\circ}\) یا \(48^{\circ}\) می باشد. زاویۀ \(QMP\) ، یعنی \((2x+20)^{\circ}\) ، برابر با \(2 \cdot 14 +20\) یا \(48^{\circ}\) خواهد بود، و \(\angle{2}\) ، یعنی متمم آن، می شود \(42^{\circ}\).
اکنون محیط لوزی \(RHOM\) را بیابید.

پاسخ این مسأله: تمامی اضلاع یک لوزی همنهشت می باشند، بنابراین \(HO\) برابر با \(x+2\) خواهد بود. و از آنجا که قطرهای یک لوزی متعامد می باشند، \(\triangle{HBO}\) یک مثلث قائم الزاویه می باشد. شما می توانید این مسأله را با قضیۀ فیثاغورث به پایان برسانید:
$$
a^2+b^2=c^2\\
(HB)^2+(BO)^2=(HO)^2\\
x^2+(x+1)^2=(x+2)^2\\
x^2+x^2+2x+1=x^2+4x+4\\
x^2-2x-3=0\\
(x-3)(x+1)=0 \\
x-3=0 \text { or } x+1=0 \\
x=3 \text { or } x=-1
$$
شما می توانید \(x=-1\) را نادیده بگیرید، زیرا منجر می شود تا یکی از ساق های \(\triangle{HBO}\) برابر با \(-1\) و ساق دیگر برابر با \(0\) گردد. بنابراین \(x\) برابر با \(3\) می باشد، که منجر می شود تا \(\overline{HR}\) دارای طول \(5\) باشد. از آنجا که لوزی ها دارای چهار ضلع همنهشت می باشند، محیط \(RHOM\) برابر با \(4 \cdot 5\) یا \(20\) واحد می باشد.
ویژگیهای کایت (kite)
کایت (شبه لوزی) موجود در شکل 9-10 را بررسی کنید و سعی کنید تا قبل از خواندن لیستی که در ادامه آمده است، ویژگیهای آن را کشف کنید.

ویژگیهای کایت به شرح زیر می باشند:
-
بنا به تعریف دو جفت جدا از هم از اضلاع متوالی همنهشت می باشند (\(\overline{JK} \cong \overline{LK}\) و \(\overline{JM} \cong \overline{LM}\)).
-
قطرها متعامد می باشند.
-
یک قطر (\(\overline{KM}\) ، قطر اصلی) عمود منصف قطر دیگر (\(\overline{JL}\) ، قطر صلیبی) می باشد. (واژگان قطر اصلی و قطر صلیبی کاملاً مفیدند، اما در کتابهای هندسی دیگر به دنبال آنها نگردید، زیرا من خودم آنها را اختراع کرده ام.)
-
قطر اصلی، یک جفت از زوایای روبروی یکدیگر را تنصیف می کند (\(\angle{K}\) و \(\angle{M}\))
-
زوایای موجود در نقاط پایانیِ قطر صلیبی همنهشت می باشند (\(\angle{J}\) , \(\angle{L}\))
سه ویژگی آخر، خواص نیمه (half properties) در کایت نامیده می شوند.
یک نوشیدنی انرژی زا بخورید و برای اثبات دیگری آماده باشید. با توجه به محدودیت جا، قصد دارم تا این بار استراتژی بازی را نادیده بگیرم. در مورد استراتژی بازی بعد از این باید به خودتان متکی باشید.

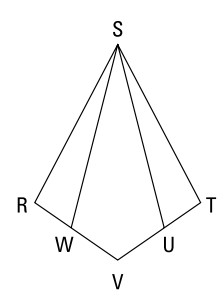
داده ها:
\(RSTV\) یک کایت با \(\overline{RS} \cong \overline{TS}\) می باشد
\(\overline{WV} \cong \overline{UV}\)
اثبات کنید:
\(\overline{WS} \cong \overline{US}\)

ترجمۀ شکل:
-
\(RSTV\) یک کایت با \(\overline{RS} \cong \overline{TS}\) می باشد
داده.
-
\(\overline{RV} \cong \overline{TV}\)
یک کایت دارای دو جفت ضلع جدا از هم و همنهشت می باشد.
-
\(\overline{WV} \cong \overline{UV}\)
داده.
-
\(\overline{RW} \cong \overline{TU}\)
اگر دو پاره خط همنهشت (\(\overline{WV}\) و \(\overline{UV}\)) از دو پاره خط همنهشت دیگر (\(\overline{RV}\) و \(\overline{TV}\)) تفریق گردند، سپس، تفاضل آنها همنهشت خواهند بود.
-
\(\angle{R} \cong \angle{T}\)
زوایای موجود در نقاط پایانی قطر صلیبی در یک کایت همنهشت می باشند.
-
\(\triangle{SRW} \cong \triangle{STU}\)
اصل SAS (گزاره های 1، 5،4).
-
\(\overline{WS} \cong \overline{US}\)
CPCTC
ویژگی های ذوزنقه و ذوزنقۀ متساوی الساقین
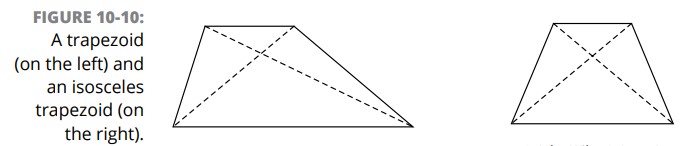
تمرینی را که برای پیش بینی ویژگیهای چهارضلعی ها در موارد قبلی داشتیم اینجا هم پیاده کنید و سعی کنید تا قبل از خواندن ویژگیها از روی شکلها، آنها را حدس بزنید (شکل 10-10). یادتان باشد: چیزی که صحیح به نظر می رسد، احتمالاً صحیح می باشد، و چیزی که صحیح به نظر نمی رسد، احتمالاً صحیح نیست.

-
ویژگیهای ذوزنقه (trapezoid) به شرح زیر می باشند:
-
قاعده ها بنا به تعریف موازی می باشند.
-
هر زاویه در قاعدۀ پایینی مکمل زاویۀ موجود در قاعدۀ بالایی در همان سمت می باشد.
-
قاعده ها بنا به تعریف موازی می باشند.
-
ویژگیهای ذوزنقۀ متساوی الساقین (isosceles trapezoid) به شرح زیر می باشد:
-
ویژگیهای ذوزنقه را بنا به تعریف شامل می گردد (قاعده های موازی).
-
بنا به تعریف، ساق ها همنهشت می باشند.
-
زوایای قاعدۀ پایین با یکدیگر همنهشت می باشند.
-
زوایای قاعدۀ بالا با یکدیگر همنهشت می باشند.
-
هر زاویه در قاعدۀ پایین با هر زاویه در قاعدۀ بالا مکمل می باشند.
-
قطرها همنهشت هستند.
-
ویژگیهای ذوزنقه را بنا به تعریف شامل می گردد (قاعده های موازی).
شاید سختترین ویژگی برای تشخیص دادن در هر دو شکل هندسی موردی است که دربارۀ زوایای مکمل می باشد. به دلیل وجود اضلاع موازی، زوایای متوالی، زوایای هم سمت داخلی می باشند و از این رو مکمل یکدیگرند. (راستی، تمامی چهارضلعی ها به جز کایت، شامل زوایای متوالی مکمل می باشند.)
در اینجا یک اثبات ذوزنقۀ متساوی الساقین برای شما داریم. در مورد استراتژی بازی دوباره به شما اعتماد می کنم تا خودتان از عهده اش برآیید.

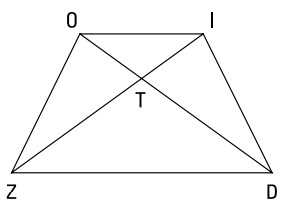
داده ها:
\(ZOID\) یک ذوزنقۀ متساوی الساقین با قاعده های \(\overline{OI}\) و \(\overline{ZD}\) می باشد
اثبات کنید:
\(\overline{TO} \cong \overline{TI}\)

ترجمۀ شکل:
-
\(ZOID\) یک ذوزنقۀ متساوی الساقین با قاعده های \(\overline{OI}\) و \(\overline{ZD}\) می باشد
داده.
-
\(\overline{ZO} \cong \overline{DI}\)
ساق های یک مثلث متساوی الساقین همنهشت می باشند.
-
\(\angle{ZOI} \cong \angle{DIO}\)
زوایای قاعدۀ بالا در ذوزنقۀ متساوی الساقین همنهشت می باشند.
-
\(\overline{OI} \cong \overline{IO}\)
خاصیت بازتابی.
-
\(\triangle{ZOI} \cong \triangle{DIO}\)
اصل SAS (گزاره های 2،3،4).
-
\(\angle{ZIO} \cong \angle{DOI}\)
CPCTC
-
\(\overline{TO} \cong \overline{TI}\)
اگر زوایا، سپس اضلاع.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: