خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
اثبات کایت بودن یک چهارضلعی
دو روش برای اثبات اینکه یک چهارضلعی کایت (شبه لوزی) می باشد: اثبات اینکه یک چهارضلعی کایت می باشد، بسیار ساده است. معمولاً، تمام چیزی که شما باید انجام دهید استفاده از مثلث های همنهشت یا مثلثهای متساوی الساقین می باشد. در اینجا دو روش داریم:

هنگام اثبات اینکه یک چهارضلعی کایت می باشد، نکات زیر ممکن است سودمند باشند:
اکنون برای یک اثبات آماده باشید:
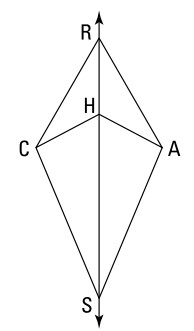
داده ها:
\(\overleftrightarrow{RS}\) نیمساز \(\angle{CRA}\) و \(\angle{CHA}\) می باشد
اثبات کنید:
\(CRAS\) یک کایت می باشد
استراتژی بازی: برنامۀ احتمالی شما برای مقابله با این اثبات می تواند این باشد:
این اثبات رسمی را بررسی کنید:

اگر تعجب کرده اید که چرا من بخشی را برای اثبات کردن اینکه یک چهارضلعی، ذوزنقه یا ذوزنقۀ متساوی الساقین می باشد، در این فصل نگنجانده ام، خوب است ـــ نشان می دهد که شما هشیار و با انرژی هستید. من این اثباتها را به این دلیل رها کرده ام که هیچ چیز جالبی در مورد آنها وجود ندارد، و از اثبات های آورده شده در این فصل آسانتر می باشند. از این گذشته، بسیار بعید است که از شما درخواست شود تا چنین اثباتی را انجام دهید. برای اطلاعات بیشتر در مورد ویژگیهای ذوزنقه ها و ذوزنقه های متساوی الساقین، فصل 10 را ببینید.

-
اگر دو جفت جدا از هم (disjoint pairs) از اضلاع متوالی در یک چهارضلعی همنهشت باشند، سپس یک کایت می باشد (معکوس تعریف کایت).
این یک تعریف است، نه یک قضیه یا اصل.
-
اگر یکی از قطرهای یک چهارضلعی عمودمنصف قطر دیگر باشد، سپس یک کایت می باشد (معکوس یک ویژگی).
هنگام اثبات اینکه یک چهارضلعی کایت می باشد، نکات زیر ممکن است سودمند باشند:
-
شکل هندسی را برای یافتن مثلث های همنهشت بررسی کنید.
در تشخیص مثلث هایی که به نظر همنهشت می آیند و تفکر در مورد چگونگی استفاده از CPCTC اهمال نورزید.
-
اولین قضیۀ متساوی الفاصله را در ذهن داشته باشید (فصل 9 را ببینید).
هنگامیکه مجبورید اثبات کنید که یک چهارضلعی کایت می باشد، ممکن است از قضیۀ متساوی الفاصله که در آن دو نقطه عمود منصف یک پاره خط را تعیین می کنند، استفاده کنید.
-
قطرها را ترسیم کنید.
یکی از روش های اثبات اینکه یک چهارضلغی کایت می باشد شامل قطرها است، بنابراین اگر شکل هندسی یک یا هر دو قطر را ندارد، سعی کنید تا یک یا هر دو قطر را ترسیم کنید.
اکنون برای یک اثبات آماده باشید:

داده ها:
\(\overleftrightarrow{RS}\) نیمساز \(\angle{CRA}\) و \(\angle{CHA}\) می باشد
اثبات کنید:
\(CRAS\) یک کایت می باشد
استراتژی بازی: برنامۀ احتمالی شما برای مقابله با این اثبات می تواند این باشد:
-
توجه داشته باشید که یکی از قطرهای این کایت از قلم افتاده است.
قطر از قلم افتاده را ترسیم کنید، \(\overline{CA}\) .
-
شکل هندسی را برای یافتن مثلث های همنهشت بررسی کنید.
بعد از ترسیم \(\overline{CA}\) ، شش جفت مثلث همنهشت خواهید داشت. دو مثلثی که به احتمال زیاد به شما کمک خواهند کرد \(\triangle{CRH}\) و \(\triangle{ARH}\) می باشند.
-
اثبات کنید که این مثلثها همنهشت می باشند.
شما می توانید از ASA استفاده کنید (فصل 9 را ببینید).
-
از قضیۀ متساوی الفاصله استفاده کنید.
با استفاده از CPCTC با \(\triangle{CRH}\) و \(\triangle{ARH}\) به \(\overline{CR} \cong \overline{AR}\) و \(\overline{CH} \cong \overline{AH}\) برسید. سپس، با استفاده از قضیۀ متساوی الفاصله، این دو جفت از اضلاع همنهشت، عمود منصف قطری را که رسم کرده اید تعیین می کند. تمام.
این اثبات رسمی را بررسی کنید:

ترجمۀ شکل:
-
ترسیم \(\overline{CA}\)
دو نقطه یک خط را تعیین می کنند.
-
\(\overleftrightarrow{RS}\) نیمساز \(\angle{CRA}\) می باشد
داده.
-
\(\angle{CRH} \cong \angle{ARH}\)
تعریف تنصیف.
-
\(\overline{RH} \cong \overline{RH}\)
خاصیت بازتابی.
-
\(\overleftrightarrow{RS}\) نیمساز \(\angle{CHA}\) می باشد
داده.
-
\(\angle{CHS} \cong \angle{AHS}\)
تعریف تنصیف.
-
\(\angle{CHR} \cong \angle{AHR}\)
اگر دو زاویه مکمل دو زاویۀ همنهشت دیگر (\(\angle{CHS}\) و \(\angle{AHS}\)) باشند، سپس آنها همنهشت می باشند.
-
\(\triangle{CRH} \cong \triangle{ARH}\)
اصل ASA (گزاره های 3،4،7).
-
\(\overline{CR} \cong \overline{AR}\)
CPCTC
-
\(\overline{CH} \cong \overline{AH}\)
CPCTC
-
\(\overleftrightarrow{RS}\) عمود منصف \(\overline{CA}\) می باشد
اگر دو نقطه (\(R\) و \(H\)) هر دو، از نقاط پایانی یک پاره خط (\(\overline{CA}\)) هم فاصله باشند، سپس آن دو نقطه عمود منصف آن پاره خط را تعیین می کنند.
-
\(CRAS\) یک کایت می باشد
اگر یکی از قطرهای یک چهارضلعی (\(\overline{RS}\)) عمود منصف دیگری (\(\overline{CA}\)) باشد، سپس آن چهارضلعی یک کایت می باشد.
اگر تعجب کرده اید که چرا من بخشی را برای اثبات کردن اینکه یک چهارضلعی، ذوزنقه یا ذوزنقۀ متساوی الساقین می باشد، در این فصل نگنجانده ام، خوب است ـــ نشان می دهد که شما هشیار و با انرژی هستید. من این اثباتها را به این دلیل رها کرده ام که هیچ چیز جالبی در مورد آنها وجود ندارد، و از اثبات های آورده شده در این فصل آسانتر می باشند. از این گذشته، بسیار بعید است که از شما درخواست شود تا چنین اثباتی را انجام دهید. برای اطلاعات بیشتر در مورد ویژگیهای ذوزنقه ها و ذوزنقه های متساوی الساقین، فصل 10 را ببینید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: