خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
محاسبۀ مساحت چهارضلعی ها

در این فصل موقتاً اثبات ها را متوقف می کنیم و به سراغ مسأله هایی که اندکی بیشتر با زندگی واقعی سر و کار دارند می رویم. دلیل اینکه روی کلمۀ "اندکی" تاکید دارم اینست که اشکالی که در اینجا با آنها سر و کار خواهید داشت ـــ مانند ذوزنقه ها (trapezoids)، شش ضلعی ها (hexagons)، هشت ضلعی ها (octagons)، و حتی پانزده ضلعی ها (pentadecagons) ـــ دقیقاً چیزهایی نیستند که شما در بیرون از کلاس های ریاضی به شیوه ای عادی با آنها مواجه شوید. اما دست کم، مفاهیمی که در اینجا با آنها کار خواهید کرد ـــ به عنوان مثال، اندازه و شکل چندضلعی ها ـــ نسبتاً چیزهای رایجی هستند. تقریباً برای همه، ارتباط برقرار کردن با چیزهای بصری در دنیای واقعی شبیه این ساده تر از ارتباط برقرار کردن با اثبات ها می باشد که بیشتر در قلمرو ریاضیات محض (pure mathematics) می باشند.

من مطمئن هستم که شما قبلاً مجبور شده اید مساحت یک مربع یا مستطیل را محاسبه کنید، خواه در کلاس های ریاضی و خواهد به صورت عملی، مانند وقتیکه می خواهید مساحت یک اتاق در منزلتان را بدانید. در این بخش، شما دوباره فرمولهای مساحت مستطیل و مربع را خواهید دید، و همچنین چندین فرمول مساحت چهارضلعی جدید و مشکل تر را نیز خواهید داشت، که ممکن است قبلاً ندیده باشید.
در اینجا پنج فرمول مساحت برای هفت چهارضلعی خاص داریم. دلیل اینکه فقط پنج فرمول وجود دارد اینست که برخی از این فرمولها چندکاره هستند ـــ به عنوان مثال، شما می توانید مساحت لوزی را با فرمول کایت (شبه لوزی) بدست آورید.
فرمولهای مساحت چهارضلعی (برای اطلاعات بیشتر در مورد انواع چهارضلعی ها، فصل 10 را ببینید):
از آنجا که مربع یک نوع خاص از چهار نوع چهارضلعی می باشد ـــ متوازی الاضلاع، مستطیل، کایت، و لوزی ـــ اساساً به فرمول مساحت خودش نیاز ندارد. شما می توانید مساحت یک مربع را با استفاده از فرمول مساحت متوازی الاضلاع/مستطیل/لوزی (\(\text{base} \cdot \text{height}\)) یا فرمول مساحت کایت/لوزی (\({1\over2} d_1d_2\)) بدست آورید. با این حال، دانستن فرمول سادۀ \(A=s^2\) خوب است، و از آنجا که این فرمول بسیار مشهور است، اگر آن را در لیست بالا نمی گنجاندم، اندکی عجیب و غریب می نمود. ایضاً این مسأله در مورد فرمول مساحت مستطیل نیز صدق می کند، زیرا مستطیل نوعی از متوازی الاضلاع است.
فرمول های مساحت برای متوازی الاضلاع، کایت، و ذوزنقه، مبتنی بر فرمول مساحت مستطیل می باشند. شکل های زیر چگونگی ارتباط این سه نوع چهارضلعی به مستطیل را نشان می دهند، و در لیست زیر جزئیات بیشتری در این زمینه ارائه شده است:
این بخش به شما امکان می دهد تا خودتان را با چندین مثال بسنجید.
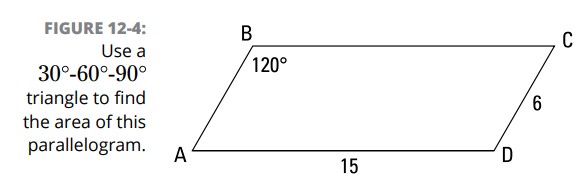
مساحت متوازی الاضلاع \(ABCD\) را در شکل 4-12 بیابید.
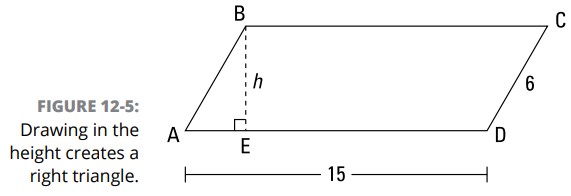
برای شروع، ارتفاع این متوازی الاضلاع را مستقیم رو به پایین از \(B\) به قاعدۀ \(\overline{AD}\) ترسیم کنید تا مشابه شکل 5-12 یک زاویۀ قائمه تشکیل شود.
زوایای متوالی در یک متوازی الاضلاع، مکمل یکدیگر می باشند. زاویۀ \(ABC\) برابر با \(120^{\circ}\) است، بنابراین \(\angle{A}\) برابر با \(60^{\circ}\) خواهد بود و از این رو \(\triangle{ABE}\) یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) است. اکنون، اگر نسبت بین اضلاع در یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) را داشته باشید، یعنی \(x:x\sqrt{3}:2x\) ، بقیۀ چیزها به سادگی یک بشکن زدن خواهند بود (برای اطلاعات بیشتر در مورد مثلث های قائم الزاویۀ خاص فصل 8 را ببینید). \(AB\) (ضلع \(2x\)) برابر با \(CD\) است ، یعنی \(6\). سپس \(AE\) (ضلع x) نیمی از آن است، یا \(3\)؛ بنابراین \(BE\) (ضلع \(x\sqrt{3}\)) می شود \(3\sqrt{3}\). در این مرحله می توانیم با فرمول مساحت متوازی الاضلاع کار را تمام کنیم:
$$
\begin{array}{c c c}
Area_{Parallelogram} & = & b \cdot h \\
&=& 15 \cdot 3\sqrt{3} \\
&=& 45\sqrt{3} \approx 77.9 \text{ units}^2
\end{array}
$$
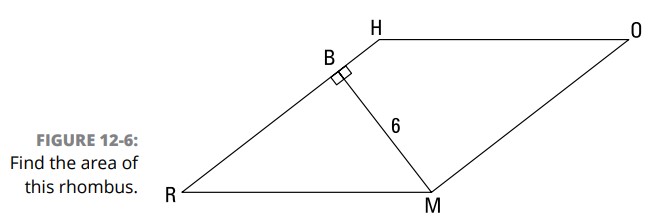
اکنون یک مسأله لوزی داریم: مساحت لوزی \(RHOM\) را با دادۀ \(MB\) برابر است با \(6\) و دانستن اینکه نسبت \(RB\) به \(BH\) برابر با \(4:1\) می باشد، بیابید (شکل 6-12 را ببینید).
این یکی اندکی مهارت آمیز است. شما ممکن است احساس کنید به اندازه کافی اطلاعات در اختیار ندارید تا این مسأله را حل کنید یا اینکه نمی دانید چگونه باید شروع کنید. اگر در هنگام حل کردن یک مسأله چنین احساسی داشتید، یک نکتۀ عالی برای شما دارم.
از آنجا که نسبت \(RB\) به \(BH\) ، \(4:1\) می باشد، شما می توانید به \(\overline{RB}\) طول \(4x\) و به \(\overline{BH}\) طول \(x\) را بدهید. سپس، از آنجا که تمامی اضلاع یک لوزی با یکدیگر همنهشت می باشند، \(RM\) باید برابر با \(RH\) باشد، بعنی برابر با \(4x+x\) یا \(5x\) . اکنون شما یک مثلث قائم الزوایه (\(\triangle{RBM}\)) با ساق های \(4x\) و \(6\) و وتر \(5x\) دارید، بنابراین می توانید از قضیۀ فیثاغورث استفاده کنید:
$$
a^2+b^2=c^2 \\
(4x)^2+6^2=(5x)^2 \\
16x^2+36=25x^2\\
36=9x^2\\
4=x^2\\
x=2 \text{ or } x =-2
$$
از آنجا که طول ضلع باید مثبت باشد، پاسخ \(x=-2\) را نادیده می گیرید. بدین ترتیب طول این ضلع، یعنی \(\overline{RH}\)، برابر با \(5 \cdot 2 = 10\) خواهد بود. (مثلث \(RBM\) دوست آشنا و قدیمی شما، یعنی مثلث \(3-4-5\) می باشد که با فاکتوری از \(2\) بزرگ شده است ـــ فصل 8 را ببینید.) اکنون از فرمول متوازی الاضلاع/لوزی برای بدست آوردن مساحت استفاده کنید:
$$ \text{Area}_{RHOM}=b \cdot h = 10 \cdot 6 = 60 \text{ units}^2 $$
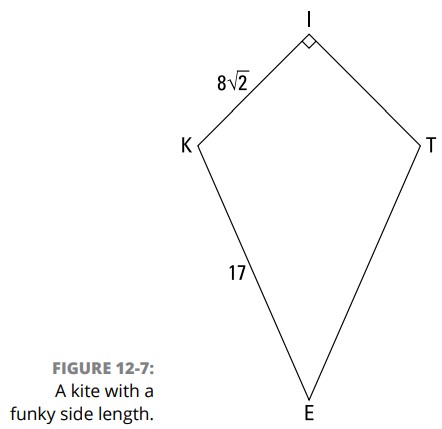
مساحت کایت \(KITE\) در شکل 7-12 را بیابید:
\(\overline{KT}\) و \(\overline{IE}\) را همانطور که در تصویر 8-12 می بینید، ترسیم کنید.
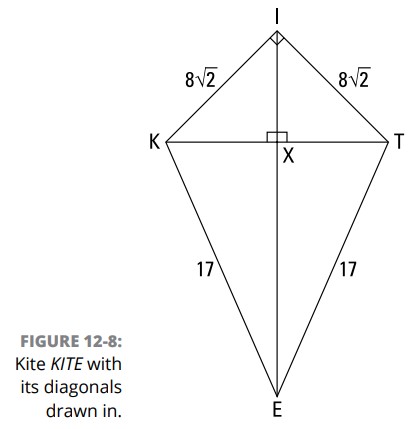
مثلث \(KIT\) یک مثلث قائم الزاویه با ساقهای همنهشت می باشد، بنابراین یک مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) با اضلاع دارای نسبت \(x:x:x\sqrt{2}\) می باشد (فصل 8 را ببینید). از این رو طول وتر آن ، \(\overline{KT}\) ، برابر است با طول ساق های آن ضربدر \(\sqrt{2}\) ؛ یعنی \(8\sqrt{2} \cdot \sqrt{2}\) یا \(16\) . \(KX\) نصف آن یا \(8\) می باشد.
مثلث \(KIX\) مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) دیگری می باشد (قطر اصلی کایت زوایای روبروی هم یعنی \(KIT\) و \(KET\) را تنصیف می کند، و نیمی از \(\angle{KIT}\) برابر با \(45^{\circ}\) است ـــ برای مشاهدۀ ویژگیهای کایت، فصل 10 را ببینید)؛ بنابراین، \(IX\)، مشابه \(KX\) ، برابر با \(8\) خواهد بود. شما مثلث قائم الزاویۀ دیگری هم دارید، \(\triangle{KXE}\) ، که یک ضلع آن \(8\) و وتر آن \(17\) می باشد. من امیدوارم زنگها برای شما به صدا در آمده باشند! شما به یک مثلث \(8-15-17\) می نگرید (فصل 8 را ببینید)، بنابراین بدون هیچ کاری، خواهید فهمید که \(XE\) برابر با \(15\) می باشد. (زنگها به صدا در نیامدند؟ نگران نباشید: شما می توانید به جای آن با استفاده از قضیۀ فیثاغورث \(XE\) را بدست آورید.) \(XE\) را با \(IX\) جمع بزنید، و برای قطر \(\overline{IE}\) به \(8+15=23\) می رسید.
اکنون که طول قطرها را می دانید، چیزی را که برای خاتمه دادن این مسأله به آن نیاز دارید، در اختیارتان می باشد. طول قطر \(\overline{KT}\) برابر با \(16\) ، و طول قطر \(\overline{IE}\) برابر با \(23\) است. این اعداد را در فرمول مساحت کایت جایگذاری کنید تا به پاسخ نهایی برسید:
$$
\text{Area}_{KITE}={1\over2}d_1d_2 ={1\over2} \cdot 16 \cdot 23 = 184 \text{ units}^2
$$
مساحت ذوزنقۀ \(TRAP\) در شکل 9-12 چقدر است؟ به نظر می رسد یک ذوزنقۀ قائم الزاویه باشد، اینطور نیست؟ فراموش نکنید ـــ ظاهر می تواند فریبنده باشد.
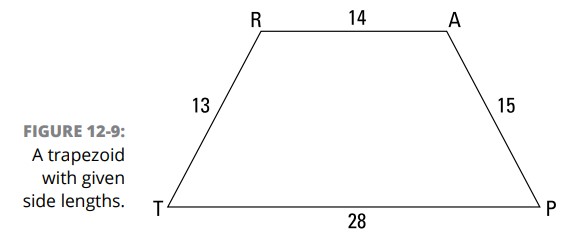
شما باید اینطور فکر کنید، زوایای قائمه، زوایای قائمه، زوایای قائمه. بنابراین دو ارتفاع را از \(R\) و \(A\) مشابه شکل 10-12 مستقیم رو به سمت پایین ترسیم کنید.
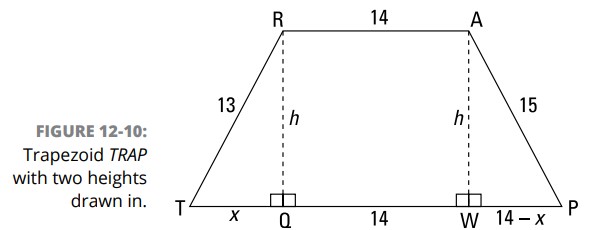
شما میتوانید ببینید که \(QW\) ، مشابه \(RA\) ، برابر با \(14\) است. سپس، از آنجا که \(TP\) برابر با \(28\) است، \(28-14\) یا \(14\) باقی می ماند، که نشان دهندۀ مجموع \(TQ\) و \(WP\) است. سپس، می توانید به \(\overline{TQ}\) طول \(x\) را نسبت بدهید، که منجر می شود تا طول \(\overline{WP}\) برابر با \(14-x\) گردد. اکنون همه چیز برای شروع آماده است ـــ بعدش چی؟ ـــ قضیۀ فیثاغورث وارد کار می شود. شما دو مجهول دارید، \(x\) و \(h\)، که باید حلشان کنید، شما نیاز به دو معادله دارید:
$$
\triangle{PAW}: (14-x)^2+h^2=15^2 \\
\triangle{TRQ}: x^2+h^2=13^2
$$
حالا، این دستگاه معادلات را حل کنید. ابتدا معادلۀ دوم را از معادلۀ اول تفریق کنید، ستون به ستون: \(x^2\) را از \((14-x)^2\) تفریق کنید، \(h^2\) را از \(h^2\) تفریق کنید (با همدیگر خط می خورند)، و \(13^2\) را از \(15^2\) تفریق کنید. سپس معادلۀ حاصله را برای بدست آوردن \(x\) حل کنید.
$$
(14-x)^2-x^2=15^2-13^2 \\
(196-28x+x^2)-x^2=225-169\\
196-28x=56\\
-28x=-140\\
x=5
$$
بنابراین \(TQ\) برابر با \(5\) می باشد، و با این حال \(\triangle{TRQ}\) نیز مثلث سه تائی فیثاغورثی دیگری می باشد ـــ مثلث \(5-12-13\) (فصل 5 را ببینید). بنابراین ارتفاع \(TRAP\) برابر با \(12\) است. (البته، شما می توانید با جایگذاری \(x=5\) در معادلات \(\triangle{TRQ}\) یا \(\triangle{PAW}\) نیز \(h\) را بدست آورید.) اکنون با فرمول مساحت ذوزنقه، کار را تمام کنید:
$$
\text{Area}_{TRAP}=\frac{b_1+b_2}{2} \cdot h=\frac{14+28}{2} \cdot 12 = 252 \text{ units}^2
$$

محاسبۀ مساحت چهارضلعی ها
من مطمئن هستم که شما قبلاً مجبور شده اید مساحت یک مربع یا مستطیل را محاسبه کنید، خواه در کلاس های ریاضی و خواهد به صورت عملی، مانند وقتیکه می خواهید مساحت یک اتاق در منزلتان را بدانید. در این بخش، شما دوباره فرمولهای مساحت مستطیل و مربع را خواهید دید، و همچنین چندین فرمول مساحت چهارضلعی جدید و مشکل تر را نیز خواهید داشت، که ممکن است قبلاً ندیده باشید.
فرمول های مساحت چهارضلعی
در اینجا پنج فرمول مساحت برای هفت چهارضلعی خاص داریم. دلیل اینکه فقط پنج فرمول وجود دارد اینست که برخی از این فرمولها چندکاره هستند ـــ به عنوان مثال، شما می توانید مساحت لوزی را با فرمول کایت (شبه لوزی) بدست آورید.
فرمولهای مساحت چهارضلعی (برای اطلاعات بیشتر در مورد انواع چهارضلعی ها، فصل 10 را ببینید):
-
مساحت مستطیل = \(\text{base} \cdot . \text{height}\) یا \(\text{length} \cdot \text{width}\) . قاعده \(\times\) ارتفاع (یا طول \(\times\) عرض، که چیز یکسانی می باشند)
-
مساحت متوازی الاضلاع = \(\text{base} \cdot . \text{height}\) . قاعده \(\times\) ارتفاع (از آنجا که لوزی هم یک نوع متوازی الاضلاع می باشد، شما می توانید از این فرمول برای لوزی نیز استفاده کنید)
-
مساحت کایت = \({1\over2} \text{diagonal}_1 \cdot \text{diagonal}_2\) . \({1\over2}\) قطر اول \(\times\) قطر دوم، یا \({1\over2}d_1d_2\) (لوزی نیز یک نوع کایت می باشد، بنابراین شما می توانید از فرمول کایت برای لوزی هم استفاده کنید)
-
مساحت مربع = یک ضلع به توان دو، یا \({1\over2}\) قطر به توان دو (\(\text{side}^2\) ، یا \({1\over2}\text{diagonal}^2\)) (فرمول دوم به این دلیل درست کار می کند که مربع یک نوع کایت می باشد)
-
مساحت ذوزنقه = \(\frac{\text{base}_1+\text{base}_2}{2} \cdot \text{height}\) = \(\text{median} \cdot \text{height}\) (قاعدۀ اول بعلاوۀ قاعدۀ دوم تقسیم بر دو و نتیجۀ این تقسیم ضربدر ارتفاع) = (میانه ضربدر ارتفاع)
نکته: میانه در یک ذوزنقه، پاره خطی است که نقاط میانی ساق ها را به یکدیگر متصل می کند. طول آن برابر است با میانگین طول قاعده ها. شما این فرمول را برای تمامی ذوزنقه ها، شامل ذوزنقه های متساوی الساقین، استفاده می کنید.
از آنجا که مربع یک نوع خاص از چهار نوع چهارضلعی می باشد ـــ متوازی الاضلاع، مستطیل، کایت، و لوزی ـــ اساساً به فرمول مساحت خودش نیاز ندارد. شما می توانید مساحت یک مربع را با استفاده از فرمول مساحت متوازی الاضلاع/مستطیل/لوزی (\(\text{base} \cdot \text{height}\)) یا فرمول مساحت کایت/لوزی (\({1\over2} d_1d_2\)) بدست آورید. با این حال، دانستن فرمول سادۀ \(A=s^2\) خوب است، و از آنجا که این فرمول بسیار مشهور است، اگر آن را در لیست بالا نمی گنجاندم، اندکی عجیب و غریب می نمود. ایضاً این مسأله در مورد فرمول مساحت مستطیل نیز صدق می کند، زیرا مستطیل نوعی از متوازی الاضلاع است.
دانستن پشت صحنۀ فرمول های مساحت چهارضلعی ها
فرمول های مساحت برای متوازی الاضلاع، کایت، و ذوزنقه، مبتنی بر فرمول مساحت مستطیل می باشند. شکل های زیر چگونگی ارتباط این سه نوع چهارضلعی به مستطیل را نشان می دهند، و در لیست زیر جزئیات بیشتری در این زمینه ارائه شده است:
-
متوازی الاضلاع (Parallelogram): در شکل 1-12 ، اگر آن مثلث کوچک موجود در سمت چپ متوازی الاضلاع را برش دهید و آن را در ناحیۀ سمت راست قرار دهید، این متوازی الاضلاع، تبدیل به یک مستطیل می شود (و مساحت آن قطعاً تغییری نمی کند). این مستطیل دارای قاعده و ارتفاع یکسانی نسبت به متوازی الاضلاع اصلی می باشد. مساحت یک مستطیل قاعده ضربدر ارتفاع می باشد، بنابراین این فرمول مساحت این متوازی الاضلاع را نیز به شما می دهد. اگر حرف مرا باور نمی کنید خودتان می توانید با قیچی یک متوازی الاضلاع کاغذی را برش دهید و این آزمایش را تجربه کنید. شکل 1-12 می تواند راهنمای شما در چگونگی انجام این آزمایش باشد.
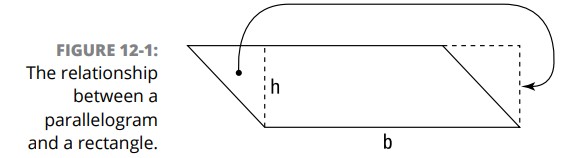
-
کایت (Kite): شکل 2-12 به شما نشان می دهد که این کایت نیمی از مساحت مستطیلی که به دور آن ترسیم شده است را دارا می باشد (این مسأله ناشی از این حقیقت می باشد که \(\triangle{1} \cong \triangle{2} \) و \(\triangle{3} \cong \triangle{4}\) ، و به همین ترتیب). شما میتوانید ببینید که طول و عرض این مستطیل بزرگ با طول قطرهای این کایت برابر می باشند. از این رو، مساحت این مستطیل (\(\text{length} \cdot \text{width}\)) ، برابر است به \(d_1d_2\) ، و از آنجا که این کایت نیمی از مساحت این مستطیل را دارا می باشد، مساحت آن می شود \({1\over2}d_1d_2\) .
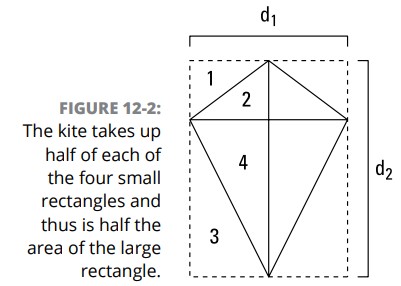
-
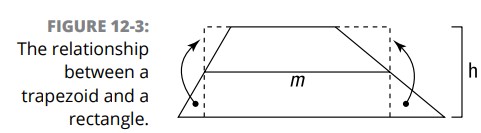
ذوزنقه (Trapezoid): اگر دو مثلثی را که در شکل 3-12 به شما نشان داده ام برش دهید و به محل های مشخص شده با نقطه چین منتقل کنید، این ذوزنقه به یک مستطیل تبدیل می گردد. این مستطیل ارتفاع یکسانی با این ذوزنقه دارد، و قاعدۀ آن برابر است با میانه (median) این ذوزنقه. از این رو، مساحت این مستطیل (و همچنین مساحت این ذوزنقه)، برابر است با میانه ضربدر ارتفاع (\(\text{median} \cdot \text{height}\)) .
چندین مسأله مساحت
این بخش به شما امکان می دهد تا خودتان را با چندین مثال بسنجید.
کلید بسیاری از مسأله های مساحت چهارضلعی اینست که ارتفاع ها (altitudes) و سایر پاره خطهای متعامد را بر روی شکل هندسیِ مسأله ترسیم کنید. انجام این کار یک یا چند زاویۀ قائمه را می سازد، که شما را قادر می سازد تا از قضیۀ فیثاغورث یا دانشتان در مورد مثلثهای قائم الزاویۀ خاص، مانند مثلث هایِ \(45^{\circ}-45^{\circ}-90^{\circ}\) و \(30^{\circ}-60^{\circ}-90^{\circ}\) استفاده کنید (فصل 8 را ببینید).
شناسایی مثلث های قائم الزاویۀ خاص در یک مسألۀ متوازی الاضلاع
مساحت متوازی الاضلاع \(ABCD\) را در شکل 4-12 بیابید.

هنگامی که یک زاویۀ \(120^{\circ}\) در یک مسأله می بینید، احتمالاً یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) آنجا مخفی شده است. (البته، یک زاویۀ \(30^{\circ}\) یا \(60^{\circ}\) نیز یک سرنخ آشکار از وجود یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) می باشد.) و اگر یک زاویۀ \(135^{\circ}\) ببینید، احتمالاً یک مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) آنجا کمین کرده باشد.
برای شروع، ارتفاع این متوازی الاضلاع را مستقیم رو به پایین از \(B\) به قاعدۀ \(\overline{AD}\) ترسیم کنید تا مشابه شکل 5-12 یک زاویۀ قائمه تشکیل شود.

زوایای متوالی در یک متوازی الاضلاع، مکمل یکدیگر می باشند. زاویۀ \(ABC\) برابر با \(120^{\circ}\) است، بنابراین \(\angle{A}\) برابر با \(60^{\circ}\) خواهد بود و از این رو \(\triangle{ABE}\) یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) است. اکنون، اگر نسبت بین اضلاع در یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) را داشته باشید، یعنی \(x:x\sqrt{3}:2x\) ، بقیۀ چیزها به سادگی یک بشکن زدن خواهند بود (برای اطلاعات بیشتر در مورد مثلث های قائم الزاویۀ خاص فصل 8 را ببینید). \(AB\) (ضلع \(2x\)) برابر با \(CD\) است ، یعنی \(6\). سپس \(AE\) (ضلع x) نیمی از آن است، یا \(3\)؛ بنابراین \(BE\) (ضلع \(x\sqrt{3}\)) می شود \(3\sqrt{3}\). در این مرحله می توانیم با فرمول مساحت متوازی الاضلاع کار را تمام کنیم:
$$
\begin{array}{c c c}
Area_{Parallelogram} & = & b \cdot h \\
&=& 15 \cdot 3\sqrt{3} \\
&=& 45\sqrt{3} \approx 77.9 \text{ units}^2
\end{array}
$$
استفاده از مثلثها و نسبتها در یک مسألۀ لوزی
اکنون یک مسأله لوزی داریم: مساحت لوزی \(RHOM\) را با دادۀ \(MB\) برابر است با \(6\) و دانستن اینکه نسبت \(RB\) به \(BH\) برابر با \(4:1\) می باشد، بیابید (شکل 6-12 را ببینید).

این یکی اندکی مهارت آمیز است. شما ممکن است احساس کنید به اندازه کافی اطلاعات در اختیار ندارید تا این مسأله را حل کنید یا اینکه نمی دانید چگونه باید شروع کنید. اگر در هنگام حل کردن یک مسأله چنین احساسی داشتید، یک نکتۀ عالی برای شما دارم.
اگر در میانۀ حل کردن یک مسألۀ هندسی ـــ یا هر مسألۀ ریاضی دیگر ـــ گیر کردید، کاری انجام دهید، هر کاری که شده! از هر جایی که می توانید آغاز کنید: از اطلاعات داده شده یا هر ایدۀ دیگری که دارید استفاده کنید (قبل از اینکه به سراغ ایده های پیچیده تر بروید، ایده های ساده تر را امتحان کنید) و چیزی بنویسید. اگر شکل هندسی ندارید، یکی ترسیم کنید. چیزی را روی کاغذ بنویسید. یک ایده می تواند ماشۀ ایدۀ دیگری را بچکاند، و قبل از اینکه بدانید، مسأله را حل کرده اید. این نکته به طرز شگفت آوری موثر است.
از آنجا که نسبت \(RB\) به \(BH\) ، \(4:1\) می باشد، شما می توانید به \(\overline{RB}\) طول \(4x\) و به \(\overline{BH}\) طول \(x\) را بدهید. سپس، از آنجا که تمامی اضلاع یک لوزی با یکدیگر همنهشت می باشند، \(RM\) باید برابر با \(RH\) باشد، بعنی برابر با \(4x+x\) یا \(5x\) . اکنون شما یک مثلث قائم الزوایه (\(\triangle{RBM}\)) با ساق های \(4x\) و \(6\) و وتر \(5x\) دارید، بنابراین می توانید از قضیۀ فیثاغورث استفاده کنید:
$$
a^2+b^2=c^2 \\
(4x)^2+6^2=(5x)^2 \\
16x^2+36=25x^2\\
36=9x^2\\
4=x^2\\
x=2 \text{ or } x =-2
$$
از آنجا که طول ضلع باید مثبت باشد، پاسخ \(x=-2\) را نادیده می گیرید. بدین ترتیب طول این ضلع، یعنی \(\overline{RH}\)، برابر با \(5 \cdot 2 = 10\) خواهد بود. (مثلث \(RBM\) دوست آشنا و قدیمی شما، یعنی مثلث \(3-4-5\) می باشد که با فاکتوری از \(2\) بزرگ شده است ـــ فصل 8 را ببینید.) اکنون از فرمول متوازی الاضلاع/لوزی برای بدست آوردن مساحت استفاده کنید:
$$ \text{Area}_{RHOM}=b \cdot h = 10 \cdot 6 = 60 \text{ units}^2 $$
ترسیم قطرها برای یافتن مساحت یک کایت
مساحت کایت \(KITE\) در شکل 7-12 را بیابید:

اگر لازم باشد قطرها را ترسیم کنید. در مورد مسأله های مساحت کایت ها و لوزی ها (و گاهی اوقات سایر مسأله های چهارضلعی) ، قطرها تقریباً همیشه برای راه حل ضروری می باشند (زیرا زوایای قائمه را می سازند). شما باید آنها را به این شکل اضافه کنید.
\(\overline{KT}\) و \(\overline{IE}\) را همانطور که در تصویر 8-12 می بینید، ترسیم کنید.

مثلث \(KIT\) یک مثلث قائم الزاویه با ساقهای همنهشت می باشد، بنابراین یک مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) با اضلاع دارای نسبت \(x:x:x\sqrt{2}\) می باشد (فصل 8 را ببینید). از این رو طول وتر آن ، \(\overline{KT}\) ، برابر است با طول ساق های آن ضربدر \(\sqrt{2}\) ؛ یعنی \(8\sqrt{2} \cdot \sqrt{2}\) یا \(16\) . \(KX\) نصف آن یا \(8\) می باشد.
مثلث \(KIX\) مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) دیگری می باشد (قطر اصلی کایت زوایای روبروی هم یعنی \(KIT\) و \(KET\) را تنصیف می کند، و نیمی از \(\angle{KIT}\) برابر با \(45^{\circ}\) است ـــ برای مشاهدۀ ویژگیهای کایت، فصل 10 را ببینید)؛ بنابراین، \(IX\)، مشابه \(KX\) ، برابر با \(8\) خواهد بود. شما مثلث قائم الزاویۀ دیگری هم دارید، \(\triangle{KXE}\) ، که یک ضلع آن \(8\) و وتر آن \(17\) می باشد. من امیدوارم زنگها برای شما به صدا در آمده باشند! شما به یک مثلث \(8-15-17\) می نگرید (فصل 8 را ببینید)، بنابراین بدون هیچ کاری، خواهید فهمید که \(XE\) برابر با \(15\) می باشد. (زنگها به صدا در نیامدند؟ نگران نباشید: شما می توانید به جای آن با استفاده از قضیۀ فیثاغورث \(XE\) را بدست آورید.) \(XE\) را با \(IX\) جمع بزنید، و برای قطر \(\overline{IE}\) به \(8+15=23\) می رسید.
اکنون که طول قطرها را می دانید، چیزی را که برای خاتمه دادن این مسأله به آن نیاز دارید، در اختیارتان می باشد. طول قطر \(\overline{KT}\) برابر با \(16\) ، و طول قطر \(\overline{IE}\) برابر با \(23\) است. این اعداد را در فرمول مساحت کایت جایگذاری کنید تا به پاسخ نهایی برسید:
$$
\text{Area}_{KITE}={1\over2}d_1d_2 ={1\over2} \cdot 16 \cdot 23 = 184 \text{ units}^2
$$
استفاده از ترفند مثلث قائم الزاویه برای ذوزنقه ها
مساحت ذوزنقۀ \(TRAP\) در شکل 9-12 چقدر است؟ به نظر می رسد یک ذوزنقۀ قائم الزاویه باشد، اینطور نیست؟ فراموش نکنید ـــ ظاهر می تواند فریبنده باشد.

شما باید اینطور فکر کنید، زوایای قائمه، زوایای قائمه، زوایای قائمه. بنابراین دو ارتفاع را از \(R\) و \(A\) مشابه شکل 10-12 مستقیم رو به سمت پایین ترسیم کنید.

شما میتوانید ببینید که \(QW\) ، مشابه \(RA\) ، برابر با \(14\) است. سپس، از آنجا که \(TP\) برابر با \(28\) است، \(28-14\) یا \(14\) باقی می ماند، که نشان دهندۀ مجموع \(TQ\) و \(WP\) است. سپس، می توانید به \(\overline{TQ}\) طول \(x\) را نسبت بدهید، که منجر می شود تا طول \(\overline{WP}\) برابر با \(14-x\) گردد. اکنون همه چیز برای شروع آماده است ـــ بعدش چی؟ ـــ قضیۀ فیثاغورث وارد کار می شود. شما دو مجهول دارید، \(x\) و \(h\)، که باید حلشان کنید، شما نیاز به دو معادله دارید:
$$
\triangle{PAW}: (14-x)^2+h^2=15^2 \\
\triangle{TRQ}: x^2+h^2=13^2
$$
حالا، این دستگاه معادلات را حل کنید. ابتدا معادلۀ دوم را از معادلۀ اول تفریق کنید، ستون به ستون: \(x^2\) را از \((14-x)^2\) تفریق کنید، \(h^2\) را از \(h^2\) تفریق کنید (با همدیگر خط می خورند)، و \(13^2\) را از \(15^2\) تفریق کنید. سپس معادلۀ حاصله را برای بدست آوردن \(x\) حل کنید.
$$
(14-x)^2-x^2=15^2-13^2 \\
(196-28x+x^2)-x^2=225-169\\
196-28x=56\\
-28x=-140\\
x=5
$$
بنابراین \(TQ\) برابر با \(5\) می باشد، و با این حال \(\triangle{TRQ}\) نیز مثلث سه تائی فیثاغورثی دیگری می باشد ـــ مثلث \(5-12-13\) (فصل 5 را ببینید). بنابراین ارتفاع \(TRAP\) برابر با \(12\) است. (البته، شما می توانید با جایگذاری \(x=5\) در معادلات \(\triangle{TRQ}\) یا \(\triangle{PAW}\) نیز \(h\) را بدست آورید.) اکنون با فرمول مساحت ذوزنقه، کار را تمام کنید:
$$
\text{Area}_{TRAP}=\frac{b_1+b_2}{2} \cdot h=\frac{14+28}{2} \cdot 12 = 252 \text{ units}^2
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: