خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
یافتن مساحت چندضلعی های منتظم

اگر شما سخت مشتاقید تا چگونگی بدست آوردن مساحت علامت ایست هشت ضلعی معمولی را بدانید، در جای درستی قرار گرفته اید. (راستی، آیا می دانستید که هر کدام از اضلاع یک علامت ایست معمولی در حدود \(12.5\) اینچ طول دارد؟ باور کردنش سخت است، اما صحت دارد.) در این بخش، شما چگونگی یافتن مساحت مثلث های متساوی الاضلاع (equilateral triangles)، شش ضلعی ها (hexagons)، هشت ضلعی ها (octagons)، و سایر شکل هایی که دارای اضلاع و زوایای برابر می باشند را درخواهید یافت.

یک چندضلعی منتظم (regular polygon) متساوی الاضلاع و متساوی الزوایا می باشد. برای یافتن مساحت یک چندضلعی منتظم، از ارتفاع آن (apothem) ـــ یک پاره خط که مرکز آن چندضلعی را به نقطۀ میانی تمامی اضلاع آن مرتبط می کند و بر روی هر ضلع عمود می باشد ـــ استفاده می کنید (در شکل 11-12 ، \(\overline{HM}\) ارتفاع یک چندضلعی می باشد).
نکته: این فرمول معمولاً به شکل \({1\over2}ap\) نوشته می شود، اگر تعریف از خود نباشد، روشی که من آن را نوشته ام، \({1\over2}pa\) ، بهتر است. من این روش نگارش آن را دوست دارم، زیرا این فرمول بر مبنای فرمول مساحت مثلث، \({1\over2}bh\) ، می باشد: محیط چندضلعی (\(p\)) با قاعدۀ مثلث (\(b\))، مرتبط است و ارتفاع چندضلعی (\(a\)) به ارتفاع مثلث (\(h\)) مرتبط است.
یک مثلث متساوی الاضلاع یک چندضلعی منتظم با کمترین تعداد اضلاع ممکن می باشد. برای محاسبۀ مساحت آن، می توانید از فرمول چندضلعی منتظم استفاده کنید؛ با این حال، دارای فرمول مساحت خودش نیز می باشد (که ممکن است آن را از فصل 7 به یاد داشته باشید):
در اینجا اولین مسأله چندضلعی منتظم شما را داریم: مساحت یک شش ضلعی منتظم با ارتفاع \(10\sqrt{3}\) چقدر می باشد؟
ابتدا، این شش ضلعی را همراه با سه قطر آن ترسیم کنید، و شش مثلث متساوی الاضلاع بسازید. سپس یک ارتفاع ترسیم کنید، که از مرکز به نقطۀ میانی یکی از اضلاع می رود. شکل 11-12 شش ضلعی \(EXAGON\) را به شما نشان می دهد.
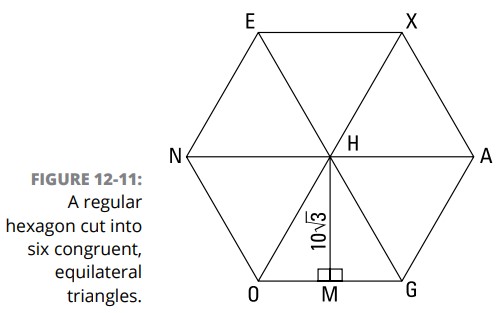
توجه داشته باشید که این ارتفاع، \(\triangle{OHG}\) را به دو مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) تقسیم می کند (دو نیمۀ یک مثلث متساوی الاضلاع ـــ فصل 8 را ببینید.) ارتفاع ساق بلندتر از مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) می باشد (ضلع \(x\sqrt{3}\)) ، بنابراین:
$$
x\sqrt{3}=10\sqrt{3} \\
x=10
$$
\(\overline{OM}\) ساق کوتاهتر (ضلع \(x\)) می باشد، بنابراین طول آن برابر با \(10\) است. \(\overline{OG}\) دو برابر آن یعنی \(20\) می باشد. و محیط شش برابر آن یعنی \(120\) می باشد.
اکنون می توانید با فرمول چندضلعی منتظم و یا فرمول مثلث متساوی الاضلاع (که در \(6\) ضرب شده است)، این مسأله را تکمیل کنید. هر دو آنها به یک اندازه آسان می باشند. انتخابتان را انجام دهید. در اینجا نتیجۀ فرمول چندضلعی منتظم را می بینید:
$$
\text{Area}_{EXAGON}={1\over2}pa \\
={1\over2} \cdot 120 \cdot 10\sqrt{3} \\
=600\sqrt{3} \text{ units}^2
$$
و در اینجا نتیجۀ استفاده از فرمول مثلث متساوی الاضلاع را می بینید:
$$
\text{Area}_{\triangle{HOG}} = \frac{s^2\sqrt{3}}{4}\\
= \frac{20^2\sqrt{3}}{4}\\
=100\sqrt{3} \text{ units}^2
$$
\(EXAGON\) شش برابر \(\triangle{HOG}\) می باشد، بنابراین خواهیم داشت:
$$
6 \cdot 100\sqrt{3} = 600\sqrt{3} \text{ units}^2
$$
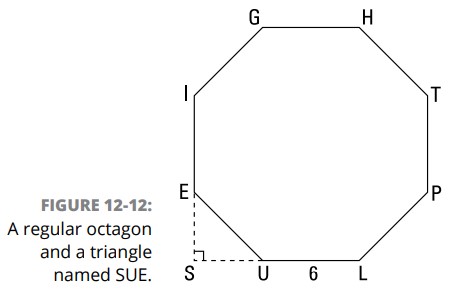
این مسألۀ جذاب هشت ضلعی را بررسی کنید: \(EIGHTPLU\) در شکل 12-12 یک هشت ضلعی منتظم می باشد که طول اضلاع آن \(6\) است و \(\triangle{SUE}\) یک مثلث قائم الزاویه می باشد،
از یک اثبات پاراگرافی برای نشان دادن اینکه \(\triangle{SUE}\) یک مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) است ، استفاده کنید.
مساحت هشت ضلعی \(EIGHTPLU\) را بیابید.
در اینجا اثبات پاراگرافی را داریم: \(EIGHTPLU\) یک هشت ضلعی منتظم می باشد، بنابراین تمامی اضلاع آن همنهشت می باشند؛ از این رو، \(\angle{IEU} \cong \angle{LUE}\) . از آنجایی که مکمل های زوایای همنهشت، همنهشت می باشند، \(\angle{SEU} \cong \angle{SUE}\) ، و بنابراین \(\triangle{SUE}\) متساوی الساقین است. در پایان، \(\angle{S}\) یک زاویۀ قائمه است، بنابراین \(\triangle{SUE}\) یک مثلث متساوی الساقین قائمه می باشد و بنابراین یک مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) می باشد.
اوکی، پس کاری که باید انجام بدهید اینست. سه مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) دیگر را در گوشه های شکل ترسیم کنید تا مشابه شکل 13-12 به یک مربع برسید.
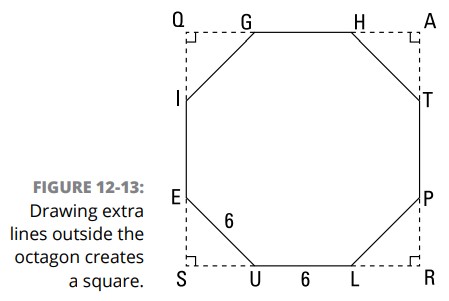
برای پیدا کردن مساحت این هشت ضلعی، صرفاً مساحت چهار مثلث کوچک موجود در گوشه های شکل را از مساحت مربع تفریق کنید. \(EU\) برابر با \(6\) است. این طول وتر (ضلع \(x\sqrt{2}\)) در مثلث \(SUE\) می باشد، بنابراین ادامه دهید و آن را برای یافتن \(x\) حل کنید:
$$
x\sqrt{2} = 6 \\
x=\frac{6}{\sqrt{2}}=3\sqrt{2}
$$
\(\overline{SU}\) یک ساق از این مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) می باشد، بنابراین یک ضلع \(x\) می باشد و از این رو دارای طول \(3\sqrt{2}\) است. همچنین \(\overline{LR}\) نیز دارای طول \(3\sqrt{2}\) است، بنابراین مربع \(SQAR\) دارای یک ضلع با طول \(3\sqrt{2}+6+3\sqrt{2}\) یا \(6+6\sqrt{2}\) واحد می باشد.
شما در مرحلۀ پایانی می باشید. ابتدا، مساحت این مربع و مساحت یکی از مثلث های گوشه را محاسبه کنید:
$$
\text{Area}_{SQAR}=s^2 \\
=(6+6\sqrt{2})^2 \\
=36+72\sqrt{2}+72 \\
=108+72\sqrt{2}
$$
$$
\text{Area}_{\triangle{SUE}}={1\over2}bh \\
={1\over2} \cdot 3\sqrt{2} \cdot 3\sqrt{2} \\
= 9
$$
برای پایان دادن به مسأله، مجموع مساحت چهار مثلث کناری را از مساحت مربع تفریق کنید:
$$
\text{Area}_{EIGHTPLU}=\text{Area}_{QAR} - 4 \cdot \text{Area}_{\triangle{SUE}} \\
= (108+72\sqrt{2}) - (4 \cdot 9) \\
= 72 + 72\sqrt{2} \approx 173.8 \text{ units}^2
$$

فرمول های مساحت چندضلعی
یک چندضلعی منتظم (regular polygon) متساوی الاضلاع و متساوی الزوایا می باشد. برای یافتن مساحت یک چندضلعی منتظم، از ارتفاع آن (apothem) ـــ یک پاره خط که مرکز آن چندضلعی را به نقطۀ میانی تمامی اضلاع آن مرتبط می کند و بر روی هر ضلع عمود می باشد ـــ استفاده می کنید (در شکل 11-12 ، \(\overline{HM}\) ارتفاع یک چندضلعی می باشد).
مساحت یک چندضلعی منتظم: برای یافتن مساحت یک چندضلعی منتظم از فرمول زیر استفاده کنید.
$$\text{Area}_{\text{Regular Polygon}}={1\over2} \text{perimeter } \cdot \text{ apothem} \text{ or } {1\over2}pa$$
\({1\over2}\) \(\times\) محیط \(\times\) ارتفاع
$$\text{Area}_{\text{Regular Polygon}}={1\over2} \text{perimeter } \cdot \text{ apothem} \text{ or } {1\over2}pa$$
\({1\over2}\) \(\times\) محیط \(\times\) ارتفاع
نکته: این فرمول معمولاً به شکل \({1\over2}ap\) نوشته می شود، اگر تعریف از خود نباشد، روشی که من آن را نوشته ام، \({1\over2}pa\) ، بهتر است. من این روش نگارش آن را دوست دارم، زیرا این فرمول بر مبنای فرمول مساحت مثلث، \({1\over2}bh\) ، می باشد: محیط چندضلعی (\(p\)) با قاعدۀ مثلث (\(b\))، مرتبط است و ارتفاع چندضلعی (\(a\)) به ارتفاع مثلث (\(h\)) مرتبط است.
یک مثلث متساوی الاضلاع یک چندضلعی منتظم با کمترین تعداد اضلاع ممکن می باشد. برای محاسبۀ مساحت آن، می توانید از فرمول چندضلعی منتظم استفاده کنید؛ با این حال، دارای فرمول مساحت خودش نیز می باشد (که ممکن است آن را از فصل 7 به یاد داشته باشید):
مساحت یک مثلث متساوی الاضلاع: در اینجا فرمول مساحت یک مثلث متساوی الاضلاع را داریم.
$$
\text{Area}_{\text{Equilateral }\triangle{}}=\frac{s^2\sqrt{3}}{4}
$$
در این فرمول \(s\) طول هر کدام از اضلاع این مثلث می باشد.
$$
\text{Area}_{\text{Equilateral }\triangle{}}=\frac{s^2\sqrt{3}}{4}
$$
در این فرمول \(s\) طول هر کدام از اضلاع این مثلث می باشد.
مسألۀ مساحت شش ضلعی
در اینجا اولین مسأله چندضلعی منتظم شما را داریم: مساحت یک شش ضلعی منتظم با ارتفاع \(10\sqrt{3}\) چقدر می باشد؟
در مورد شش ضلعی ها، از \(30^{\circ}-60^{\circ}-90^{\circ}\) و مثلث های متساوی الاضلاع، استفاده کنید. یک شش ضلعی منتظم می تواند به شش مثلث متساوی الاضلاع برش داده شود، و یک مثلث متساوی الاضلاع می تواند به دو مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) تقسیم گردد. بنابراین اگر در حال انجام یک مسألۀ شش ضلعی می باشید، ممکن است بخواهید شکل را برش دهید و از مثلث های متساوی الاضلاع یا مثلث های \(30^{\circ}-60^{\circ}-90^{\circ}\) کمک بگیرید تا ارتقاع، محیط، یا مساحت را بیابید.
ابتدا، این شش ضلعی را همراه با سه قطر آن ترسیم کنید، و شش مثلث متساوی الاضلاع بسازید. سپس یک ارتفاع ترسیم کنید، که از مرکز به نقطۀ میانی یکی از اضلاع می رود. شکل 11-12 شش ضلعی \(EXAGON\) را به شما نشان می دهد.

توجه داشته باشید که این ارتفاع، \(\triangle{OHG}\) را به دو مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) تقسیم می کند (دو نیمۀ یک مثلث متساوی الاضلاع ـــ فصل 8 را ببینید.) ارتفاع ساق بلندتر از مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) می باشد (ضلع \(x\sqrt{3}\)) ، بنابراین:
$$
x\sqrt{3}=10\sqrt{3} \\
x=10
$$
\(\overline{OM}\) ساق کوتاهتر (ضلع \(x\)) می باشد، بنابراین طول آن برابر با \(10\) است. \(\overline{OG}\) دو برابر آن یعنی \(20\) می باشد. و محیط شش برابر آن یعنی \(120\) می باشد.
اکنون می توانید با فرمول چندضلعی منتظم و یا فرمول مثلث متساوی الاضلاع (که در \(6\) ضرب شده است)، این مسأله را تکمیل کنید. هر دو آنها به یک اندازه آسان می باشند. انتخابتان را انجام دهید. در اینجا نتیجۀ فرمول چندضلعی منتظم را می بینید:
$$
\text{Area}_{EXAGON}={1\over2}pa \\
={1\over2} \cdot 120 \cdot 10\sqrt{3} \\
=600\sqrt{3} \text{ units}^2
$$
و در اینجا نتیجۀ استفاده از فرمول مثلث متساوی الاضلاع را می بینید:
$$
\text{Area}_{\triangle{HOG}} = \frac{s^2\sqrt{3}}{4}\\
= \frac{20^2\sqrt{3}}{4}\\
=100\sqrt{3} \text{ units}^2
$$
\(EXAGON\) شش برابر \(\triangle{HOG}\) می باشد، بنابراین خواهیم داشت:
$$
6 \cdot 100\sqrt{3} = 600\sqrt{3} \text{ units}^2
$$
مسألۀ مساحت هشت ضلعی
این مسألۀ جذاب هشت ضلعی را بررسی کنید: \(EIGHTPLU\) در شکل 12-12 یک هشت ضلعی منتظم می باشد که طول اضلاع آن \(6\) است و \(\triangle{SUE}\) یک مثلث قائم الزاویه می باشد،
از یک اثبات پاراگرافی برای نشان دادن اینکه \(\triangle{SUE}\) یک مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) است ، استفاده کنید.
مساحت هشت ضلعی \(EIGHTPLU\) را بیابید.
در اینجا اثبات پاراگرافی را داریم: \(EIGHTPLU\) یک هشت ضلعی منتظم می باشد، بنابراین تمامی اضلاع آن همنهشت می باشند؛ از این رو، \(\angle{IEU} \cong \angle{LUE}\) . از آنجایی که مکمل های زوایای همنهشت، همنهشت می باشند، \(\angle{SEU} \cong \angle{SUE}\) ، و بنابراین \(\triangle{SUE}\) متساوی الساقین است. در پایان، \(\angle{S}\) یک زاویۀ قائمه است، بنابراین \(\triangle{SUE}\) یک مثلث متساوی الساقین قائمه می باشد و بنابراین یک مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) می باشد.

اکنون به دنبال پاسخ بخش مساحت در مسأله می رویم. اما قبل از آن، در اینجا دو نکتۀ مهم داریم:
-
برای هشت ضلعی ها، از مثلث های \(45^{\circ}-45^{\circ}-90^{\circ}\) استفاده کنید.
اگر یک مسأله شامل یک هشت ضلعی منتظم باشد، پاره خطهایی را به شکل هندسی اضافه کنید تا یک یا بیشتر مثلث های \(45^{\circ}-45^{\circ}-90^{\circ}\) و یک مربع را بدست آورید تا برای حل مسأله به شما کمک کند.
-
خارج از چارچوب معین و به صورت خلاقانه فکر کنید.
اینکه فقط به داخل یک شکل نگاه کردن برای شما تبدیل به یک عادت گردد، آسان است، زیرا برای اکثریت قریب به اتفاق مسائل جواب می دهد. اما گاهی اوقات، شما نیاز به شکستن این عادت دارید و لازم می شود تا به خارج از محیط شکل هندسی بنگرید.
اوکی، پس کاری که باید انجام بدهید اینست. سه مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) دیگر را در گوشه های شکل ترسیم کنید تا مشابه شکل 13-12 به یک مربع برسید.

برای پیدا کردن مساحت این هشت ضلعی، صرفاً مساحت چهار مثلث کوچک موجود در گوشه های شکل را از مساحت مربع تفریق کنید. \(EU\) برابر با \(6\) است. این طول وتر (ضلع \(x\sqrt{2}\)) در مثلث \(SUE\) می باشد، بنابراین ادامه دهید و آن را برای یافتن \(x\) حل کنید:
$$
x\sqrt{2} = 6 \\
x=\frac{6}{\sqrt{2}}=3\sqrt{2}
$$
\(\overline{SU}\) یک ساق از این مثلث \(45^{\circ}-45^{\circ}-90^{\circ}\) می باشد، بنابراین یک ضلع \(x\) می باشد و از این رو دارای طول \(3\sqrt{2}\) است. همچنین \(\overline{LR}\) نیز دارای طول \(3\sqrt{2}\) است، بنابراین مربع \(SQAR\) دارای یک ضلع با طول \(3\sqrt{2}+6+3\sqrt{2}\) یا \(6+6\sqrt{2}\) واحد می باشد.
شما در مرحلۀ پایانی می باشید. ابتدا، مساحت این مربع و مساحت یکی از مثلث های گوشه را محاسبه کنید:
$$
\text{Area}_{SQAR}=s^2 \\
=(6+6\sqrt{2})^2 \\
=36+72\sqrt{2}+72 \\
=108+72\sqrt{2}
$$
$$
\text{Area}_{\triangle{SUE}}={1\over2}bh \\
={1\over2} \cdot 3\sqrt{2} \cdot 3\sqrt{2} \\
= 9
$$
برای پایان دادن به مسأله، مجموع مساحت چهار مثلث کناری را از مساحت مربع تفریق کنید:
$$
\text{Area}_{EIGHTPLU}=\text{Area}_{QAR} - 4 \cdot \text{Area}_{\triangle{SUE}} \\
= (108+72\sqrt{2}) - (4 \cdot 9) \\
= 72 + 72\sqrt{2} \approx 173.8 \text{ units}^2
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: