خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
قضیۀ ارتفاع وارد بر وتر
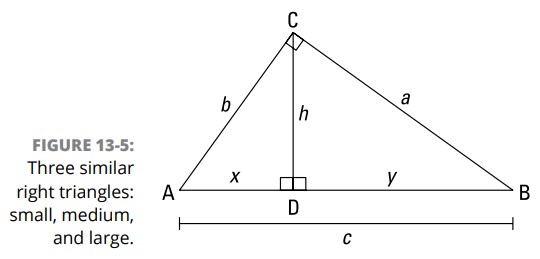
در یک مثلث قائم الزاوایه، ارتفاعی که بر وتر عمود می باشد دارای یک ویژگی خاص است: این ارتفاع دو مثلث قائم الزاویۀ کوچکتر را می سازد که هر دوی آنها با مثلث قائم الزاویۀ اصلی متشابه می باشند.

توجه داشته باشید که دو معادلۀ ارائه شده در آیتم سوم از لیست بالا، در واقع یک مفهوم می باشند و نه دو چیز جداگانه. این مفهوم بر روی هر دو ضلع مثلث بزرگتر به شکل دقیقاً یکسانی کار می کند:
$$(\text{leg of big} \triangle{})^2=(\text{part of hypotenuse below it}) \cdot (\text{whole hypotenuse})$$
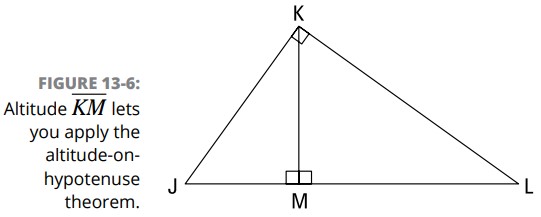
در اینجا یک مسألۀ دو بخشی برای شما داریم: از شکل 6-13 برای پاسخ دادن به سوالات زیر استفاده کنید:
هنگامیکه مشغول حل کردن یک مسأله شامل یک شکل هندسی با ارتفاع وارد بر وتر می باشید، مفروض نگیرید که الزاماً باید از بخش دوم یا سوم قضیۀ ارتفاع وارد بر وتر استفاده کنید. گاهی اوقات، ساده ترین روش حل مسأله استفاده از قضیۀ فیثاغورث می باشد. و در مواقع دیگری، شما می توانید از نسبتهای معمولی در مثلث های متشابه برای حل کردن آن مسأله استفاده کنید.
مسألۀ بعد این نکته را نشان می دهد: از شکل زیر برای یافتن \(h\)، یعنی ارتفاع \(\triangle{ABC}\) ، استفاده کنید.
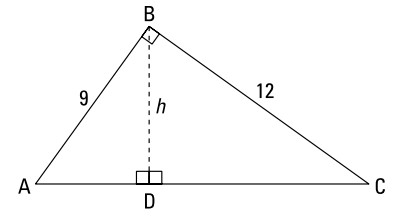
ابتدا با استفاده از قضیۀ فیثاغورث یا با توجه به اینکه شما یک مثلث از خانوادۀ \(3:4:5\) دارید ـــ مشخصاً یک مثلث \(9-12-15\) ـــ طول \(AC\) را بدست آورید. بنابراین \(AC=15\) . سپس، با وجود اینکه می توانید این مسأله را با قضیۀ ارتفاع وارد بر وتر حل کنید، آن رویکرد اندکی پیچیده تر و زمان بر تر است. در عوض، صرفاً از یک تناسب معمولی بین مثلثهای متشابه استفاده کنید:
$$
\frac{\text{Long leg}_{\triangle{ABD}}}{\text{Long leg}_{\triangle{ACB}}}=\frac{\text{hypotenus}_{\triangle{ABD}}}{\text{hypotenus}_{\triangle{ACB}}} \\
\frac{h}{12}=\frac{9}{15}\\
15h=108\\
h=7.2
$$
تمام.

قضیۀ ارتفاع وارد بر وتر (Altitude-on-Hypotenuse Theorem): اگر مشابه شکل 5-13، یک ارتفاع بر روی یک وتر در یک مثلث قائم الزاویه ترسیم شود، سپس:
-
دو مثلث قائم الزاویۀ تشکیل شده، با مثلث قائم الزوایۀ اصلی و همچنین با یکدیگر متشابه می باشند: \(\triangle{ACB} \sim \triangle{ADC} \sim \triangle{CDB}\)
-
\(h^2=xy\)
-
\(a^2=yc\) و \(b^2=xc\)
توجه داشته باشید که دو معادلۀ ارائه شده در آیتم سوم از لیست بالا، در واقع یک مفهوم می باشند و نه دو چیز جداگانه. این مفهوم بر روی هر دو ضلع مثلث بزرگتر به شکل دقیقاً یکسانی کار می کند:
$$(\text{leg of big} \triangle{})^2=(\text{part of hypotenuse below it}) \cdot (\text{whole hypotenuse})$$
ترجمۀ فرمول:
leg of big : ساق مثلث بزرگتر
part of hypotenuse below it: بخشی از وتر زیر آن
whole hypotenuse: کل وتر
leg of big : ساق مثلث بزرگتر
part of hypotenuse below it: بخشی از وتر زیر آن
whole hypotenuse: کل وتر

در اینجا یک مسألۀ دو بخشی برای شما داریم: از شکل 6-13 برای پاسخ دادن به سوالات زیر استفاده کنید:

-
اگر \(JL=17\) و \(KL=15\) ، اندازه های \(JK\) ، \(JM\) ، \(ML\) ، و \(KM\) چقدر می باشند؟
در اینجا چگونگی حل این مسأله را می بینید: \(JK\) برابر با \(8\) می باشد، زیرا شما یک مثلث \(8-15-17\) دارید (یا شما می توانید با قضیۀ فیثاغورث به \(JK\) برسید؛ برای اطلاعات بیشتر فصل 8 را ببینید).
اکنون می توانید با استفاده از بخش سوم قضیۀ ارتفاع وارد بر وتر، \(JM\) و \(ML\) را بیابید:
$$
(JK)^2=(JM)(JL) \\
8^2=JM \cdot 17 \\
JM=\frac{64}{17} \approx 3.8
$$
$$
(KL)^2=(ML)(JL)\\
15^2=ML \cdot 17 \\
ML=\frac{225}{17} \approx 13.2
$$
(من پاسخ \(ML\) را به این دلیل گنجاندم که مثال دیگری از این قضیه داشته باشیم، اما بدیهی است که شما صرفاً با تفریق \(JM\) از \(JL\) می توانستید خیلی ساده به \(ML\) برسید.) در آخر از بخش دوم این قضیه (و یا اگر ترجیح می دهید از قضیۀ فیثاغورث) برای بدست آوردن \(KM\) استفاده کنید:
$$
(KM)^2=(JM)(ML) \\
(KM)^2=(\frac{64}{17})(\frac{225}{17}) \\
KM=\sqrt{\frac{14,400}{289}}=\frac{120}{17} \approx 7.1
$$
-
اگر \(ML=16\) و \(JK=15\) ، \(JM\) چقدر خواهد بود؟(توجه داشته باشید که هیچ کدام از اطلاعات پرسش 1 در مورد پرسش دوم بکار نمی رود.)
\(JM\) را برابر با \(x\) قرار دهید؛ سپس از بخش سوم این قضیه استفاده کنید.
$$
(JK)^2=(JM)(JL) \\
15^2=x(x+16) \\
225=x^2+16x \\
x^2+16x-225=0 \\
(x-9)(x+25)=0 \\
x-9=0 \text{ or } x+25=0 \\
x=9 \text{ or } x=-25
$$
شما می دانید که طول نمی تواند \(-25\) باشد، بنابراین \(JM=9\) . (اگر در فاکتورگیری این معادلۀ درجه دوم مشکل دارید می توانید از فرمول حل کردن معادلۀ درجه دوم نیز استفاده کنید.)
هنگامیکه مشغول حل کردن یک مسأله شامل یک شکل هندسی با ارتفاع وارد بر وتر می باشید، مفروض نگیرید که الزاماً باید از بخش دوم یا سوم قضیۀ ارتفاع وارد بر وتر استفاده کنید. گاهی اوقات، ساده ترین روش حل مسأله استفاده از قضیۀ فیثاغورث می باشد. و در مواقع دیگری، شما می توانید از نسبتهای معمولی در مثلث های متشابه برای حل کردن آن مسأله استفاده کنید.
مسألۀ بعد این نکته را نشان می دهد: از شکل زیر برای یافتن \(h\)، یعنی ارتفاع \(\triangle{ABC}\) ، استفاده کنید.

ابتدا با استفاده از قضیۀ فیثاغورث یا با توجه به اینکه شما یک مثلث از خانوادۀ \(3:4:5\) دارید ـــ مشخصاً یک مثلث \(9-12-15\) ـــ طول \(AC\) را بدست آورید. بنابراین \(AC=15\) . سپس، با وجود اینکه می توانید این مسأله را با قضیۀ ارتفاع وارد بر وتر حل کنید، آن رویکرد اندکی پیچیده تر و زمان بر تر است. در عوض، صرفاً از یک تناسب معمولی بین مثلثهای متشابه استفاده کنید:
$$
\frac{\text{Long leg}_{\triangle{ABD}}}{\text{Long leg}_{\triangle{ACB}}}=\frac{\text{hypotenus}_{\triangle{ABD}}}{\text{hypotenus}_{\triangle{ACB}}} \\
\frac{h}{12}=\frac{9}{15}\\
15h=108\\
h=7.2
$$
تمام.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: