خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مبانی دایره
از جهتی، دایره ساده ترین همۀ اشکال می باشد ـــ یک منحنی نرم که همواره دارای فاصلۀ یکسانی تا مرکز دایره می باشد: بدون گوشه ها، بدون بی نظمی ها، تفاوتی نمی کند چگونه آن را بچرخانید، همیشه همان شکل ساده را خواهد داشت. از سوی دیگر، این منحنی ساده شامل عدد \(pi (\pi=3.14159...)\) می باشد، و هیچ چیز ساده ای در مورد آن وجود ندارد. این عدد بدون هیچ الگوی تکراری از ارقام، تا ابد ادامه می یابد. با وجود این واقعیت که ریاضیدانان دایره و عدد \(\pi\) را بیش از 2000 سال مورد مطالعه قرار داده اند، اسرار حل نشدۀ بسیاری در مورد آنها باقی مانده است.

همچنین دایره، شاید، رایجترین شکل در جهان طبیعی باشد (اگر کره ها را بشمارید، که البته مدور می باشند و سطح رویۀ آنها شامل بی نهایت مجموعه از دایره ها می باشد). تعداد \(10^{21}\) (یا \(1,000,000,000,000,000,000,000\)) ستاره در جهان وجود دارند که همگی کروی شکل می باشند. قطرات کوچک آب در یک ابر کروی شکل می باشد (یک ابر می تواند شامل تریلیون ها قطره باشد). یک سنگ را در حوضچه ای بیندازید، امواج در شکل حلقه های مدور گسرش می یابند. زمین در یک مدار مدور به دور خورشید می گردد (اوکی، اگر شما یک خُرده گیر اهل نجوم هستید شکل دقیق آن بیضی است؛ با این حال بسیار به دایره نزدیک است). و دقیقاً در همین لحظه، شما مشغول مسافرت همراه با کرۀ زمین می باشید که در یک مسیر مدور به دور خودش می چرخد.
در این فصل، برخی از اساسی ترین ویژگی های دایره را بررسی می کنید. زمان شروع فرا رسیده است.
من شک دارم که شما نیاز به تعریفی برای دایره داشته باشید، اما برای آن دسته از شما که عاشق صحبت کردن به زبان ریاضی می باشید، در اینجا تعریف آن را داریم.
در ادامه در مورد سه نوع اصلی از پاره خطهایی که درون یک دایره می توانید ببابید، صحبت خواهم کرد: شعاع ها (radii)، وتر ها (chords)، و قطرها (diameters). اگرچه شروع کردن با این چیزهای مستقیم در فصلی که مربوط به دایره های دارای انحنا است، ممکن است اندکی عجیب به نظر برسد، اما برخی از جذابترین و مهمترین قضایای مربوط به دایره ها از این سه پاره خط آغاز می گردند. شما بعداً می توانید این قضایا را با چندین مسأله دایره بررسی کنید.
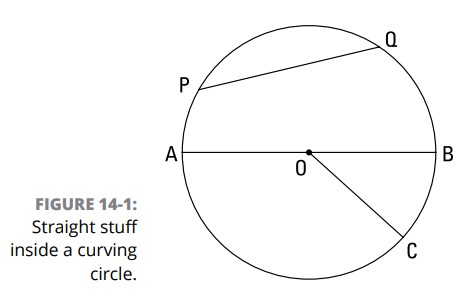
شکل 1-14 دایرۀ \(O\) را همراه با قطر \(\overline{AB}\) (که همچنین یک وتر نیز می باشد)، شعاع های \(\overline{OA}\) ، \(\overline{OB}\) ، و \(\overline{OC}\) ، و وتر \(\overline{PQ}\) را به شما نشان می دهد.
در این بخش با پنج قضیۀ مهم در مورد ویژگیهای پاره خطهای درون یک دایره آشنا خواهید شد. این قضایا در مورد شعاع ها و وترها چیزهایی را به شما می گویند (توجه داشته باشید که دو تا از این قضایا در هر دو جهت درست کار می کنند):
در اینجا یک اثبات داریم که سه تا از قضایای نامبرده شده در بخش قبلی را استفاده می کند:
داده ها:
دایرۀ \(G\)
\(F\) نقطۀ میانی \(\overline{AE}\) می باشد
\(\overline{GB} \bot \overline{CA}\)
\(\overline{GD} \bot \overline{CE}\)
اثبات کنید:
\(BCDG\) یک کایت می باشد
قبل از اینکه این اثبات را بخوانید، ممکن است بخواهید استراتژی بازی خودتان را داشته باشید.

در هنگام حل کردن مسأله های دایره، سه چیز مهم می باشد، شعاع، شعاع، و باز هم شعاع! دلیل اینگونه مطرح کردن تاکید بر روی اهمیت شعاع می باشد. بسیار مهم است که به تمامی شعاع ها در یک مسألۀ دایره توجه کنید و بررسی کنید که در کجاهای شکل هندسی مسأله می توانید شعاع های دیگری را بیفزایید. معمولاً به اضافه کردن شعاع ها نیاز دارید تا مثلث های قائم الزاویه یا متساوی الساقین را بسازید تا از آنها برای حل مسأله استفاده کنید. کاری که انجام می دهید همراه با جزئیات بیشتر در اینجا آمده است:
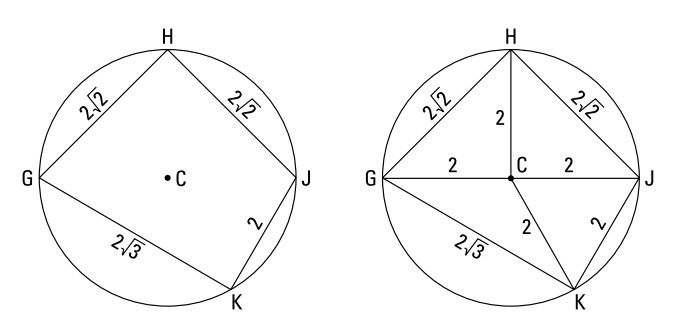
اکنون این مسأله را بررسی کنید: مساحت چهارضلعی محاط شدۀ \(GHJK\) که در شکل سمت چپ نشان داده شده است را بیابید. این دایره دارای شعاع \(2\) می باشد.
در اینجا نکته ای داریم که منجر می شود، دو راهنمایی به شما ارائه شود. اولین راهنما اینکه همانطور که در شکل سمت راست می بینید، چهار شعاع را به چهار رأس این چهارضلعی ترسیم کنید.
اکنون به سادگی فقط نیاز دارید تا مساحت هر مثلث را به صورت جداگانه بیابید. شما می توانید ببینید که \(\triangle{JKC}\) متوازی الاضلاع می باشد، بنابراین می توانید از فرمول مساحت مثلث متوازی الاضلاع برای آن استفاده کنید (این فرمول در فصل 7 ارائه شده است):
$$Area_{\triangle{JKC}} = \frac{s^2\sqrt{3}}{4}= \frac{2^2\sqrt{3}}{4}=\sqrt{3} \text{ units}^2$$
و اگر حواستان جمع باشد، باید مثلثهای \(GHC\) و \(HJC\) را شناسایی کرده باشید. اضلاع آنها در نسبت \(2:2:2\sqrt{2}\) می باشند، که به \(1:1:\sqrt{2}\) کاهش می یابد؛ از این رو، آنها مثلثهای \(45^{\circ}-45^{\circ}-90^{\circ}\) می باشند (فصل 8 را ببینید). شما هم اکنون قاعده و ارتفاع این مثلث ها را می دانید، بنابراین رسیدن به مساحت آنها به سادگیِ یک بشکن زدن می باشد. برای هر کدام از این مثلثها داریم:
$$Area=\frac{1}{2}bh=\frac{1}{2} \cdot 2 \cdot 2 = 2 \text{ units}^2$$
راهنمای دیگری که می تواند به شما کمک کند در ارتباط با \(\triangle{KGC}\) می باشد. ارتفاع آن را ترسیم کنید، برای ترسیم ارتفاع بخشی از شعاع آن را از مرکز دایره، یعنی \(C\)، به \(\overline{GK}\) ترسیم کنید. این شعاع بر \(\overline{GK}\) عمود می باشد و از این رو \(\overline{GK}\) را به دو پاره خط برابر با طول \(\sqrt{3}\) تقسیم می کند. شما \(\triangle{KGC}\) را به دو مثلث قائم الزاویه تقسیم کرده اید؛ هر کدام از این مثلثها دارای وتر \(2\) و یک ساق با اندازۀ \(\sqrt{3}\) می باشند، بنابراین اندازۀ ساق دیگر (ارتفاع) برابر با \(1\) می باشد (اندازۀ این ساق را با استفاده از قضیۀ فیثاغورث و یا با شناسایی نسبت این مثلث که \(1:\sqrt{3}:2\) می باشد و در واقع یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) است، بدست می آورید). بنابراین \(\triangle{KGC}\) دارای ارتفاع \(1\) و قاعدۀ \(2\sqrt{3}\) می باشد. کافیست این مقادیر را در فرمول معمولی مساحت مثلث جایگذاری کنید:
$$Area_{\triangle{KGC}}=\frac{1}{2}bh=\frac{1}{2} \cdot 2\sqrt{3} \cdot 1 = \sqrt{3} \text{ units}^2$$
اکنون برای محاسبۀ مساحت چهارضلعی، مساحت این مثلث ها را با یکدیگر جمع می زنیم:
$$
\text{Area}_{GHIJ} = \text{area}_{\triangle{JKC}} + \text{area}_{\triangle{GHC}} + \text{area}_{\triangle{HJC}} + \text{area}_{\triangle{KGC}} \\
= \sqrt{3}+2+2+\sqrt{3} \\
= 4+2\sqrt{3} \approx 7.46 \text{ units}^2
$$

همچنین دایره، شاید، رایجترین شکل در جهان طبیعی باشد (اگر کره ها را بشمارید، که البته مدور می باشند و سطح رویۀ آنها شامل بی نهایت مجموعه از دایره ها می باشد). تعداد \(10^{21}\) (یا \(1,000,000,000,000,000,000,000\)) ستاره در جهان وجود دارند که همگی کروی شکل می باشند. قطرات کوچک آب در یک ابر کروی شکل می باشد (یک ابر می تواند شامل تریلیون ها قطره باشد). یک سنگ را در حوضچه ای بیندازید، امواج در شکل حلقه های مدور گسرش می یابند. زمین در یک مدار مدور به دور خورشید می گردد (اوکی، اگر شما یک خُرده گیر اهل نجوم هستید شکل دقیق آن بیضی است؛ با این حال بسیار به دایره نزدیک است). و دقیقاً در همین لحظه، شما مشغول مسافرت همراه با کرۀ زمین می باشید که در یک مسیر مدور به دور خودش می چرخد.
در این فصل، برخی از اساسی ترین ویژگی های دایره را بررسی می کنید. زمان شروع فرا رسیده است.
شعاع ها (Radii) و وتر ها (Chords)
من شک دارم که شما نیاز به تعریفی برای دایره داشته باشید، اما برای آن دسته از شما که عاشق صحبت کردن به زبان ریاضی می باشید، در اینجا تعریف آن را داریم.
دایره (Circle): یک دایره مجموعه ای از تمامی نقاط روی یک صفحه می باشد که از یک نقطۀ واحد (که به آن مرکز دایره می گویند) دارای فاصلۀ یکسانی باشند.
در ادامه در مورد سه نوع اصلی از پاره خطهایی که درون یک دایره می توانید ببابید، صحبت خواهم کرد: شعاع ها (radii)، وتر ها (chords)، و قطرها (diameters). اگرچه شروع کردن با این چیزهای مستقیم در فصلی که مربوط به دایره های دارای انحنا است، ممکن است اندکی عجیب به نظر برسد، اما برخی از جذابترین و مهمترین قضایای مربوط به دایره ها از این سه پاره خط آغاز می گردند. شما بعداً می توانید این قضایا را با چندین مسأله دایره بررسی کنید.
تعریف شعاع، وتر، و قطر
در اینجا سه اصطلاح داریم که برای تحقیقات شما در مورد دایره، بنیادی می باشند:
-
شعاع (Radius): یک شعاع در یک دایره ـــ فاصلۀ بین مرکز آن تا یک نقطه بر روی آن دایره ـــ اندازۀ دایره را به شما می گوید. یک شعاع، علاوه بر اینکه اندازه ای برای فاصله می باشد، همچنین یک پاره خط است که از مرکز دایره به یک نقطه بر روی دایره می رود.
-
وتر (Chord): یک پاره خط که دو نقطه بر روی یک دایره را به یکدیگر متصل می کند، یک وتر از آن دایره نامیده می شود.
-
قطر (Diameter): یک وتر که از مرکز یک دایره عبور می کند یک قطر از آن دایره نامیده می شود. طول قطر یک دایره دو برابر طول شعاع آن می باشد.
شکل 1-14 دایرۀ \(O\) را همراه با قطر \(\overline{AB}\) (که همچنین یک وتر نیز می باشد)، شعاع های \(\overline{OA}\) ، \(\overline{OB}\) ، و \(\overline{OC}\) ، و وتر \(\overline{PQ}\) را به شما نشان می دهد.

معرفی پنج قضیه در مورد دایره
در این بخش با پنج قضیۀ مهم در مورد ویژگیهای پاره خطهای درون یک دایره آشنا خواهید شد. این قضایا در مورد شعاع ها و وترها چیزهایی را به شما می گویند (توجه داشته باشید که دو تا از این قضایا در هر دو جهت درست کار می کنند):
-
اندازۀ شعاع ها (Radii size): تمامی شعاع های یک دایره همنهشت می باشند.
-
تعامد و وترهای تنصیف شده (Perpendicularity and bisected chords):
-
اگر یک شعاع بر روی یک وتر عمود باشد، آن گاه آن وتر را تنصیف می کند.
-
اگر یک شعاع، یک وتر (که یک قطر نباشد) را تنصیف کند، آن گاه بر روی آن وتر عمود است.
-
اگر یک شعاع بر روی یک وتر عمود باشد، آن گاه آن وتر را تنصیف می کند.
-
فاصله و اندازۀ وتر (Distance and chord size):
-
اگر دو وتر در یک دایره، دارای فاصلۀ یکسانی از مرکز آن دایره باشند، آن گاه با یکدیگر همنهشتند.
-
اگر دو وتر در یک دایره، همنهشت باشند، آن گاه از مرکز آن دایره فاصلۀ یکسانی دارند.
-
اگر دو وتر در یک دایره، دارای فاصلۀ یکسانی از مرکز آن دایره باشند، آن گاه با یکدیگر همنهشتند.
یک مسأله اثبات در مورد دایره ها
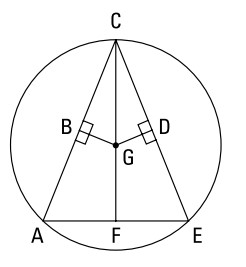
در اینجا یک اثبات داریم که سه تا از قضایای نامبرده شده در بخش قبلی را استفاده می کند:

داده ها:
دایرۀ \(G\)
\(F\) نقطۀ میانی \(\overline{AE}\) می باشد
\(\overline{GB} \bot \overline{CA}\)
\(\overline{GD} \bot \overline{CE}\)
اثبات کنید:
\(BCDG\) یک کایت می باشد
قبل از اینکه این اثبات را بخوانید، ممکن است بخواهید استراتژی بازی خودتان را داشته باشید.

ترجمۀ شکل:
-
دایرۀ \(G\)
\(F\) نقطۀ میانی \(\overline{AE}\) می باشد
داده.
-
\(\overline{AF} \cong \overline{EF}\)
تعریف نقطۀ میانی.
-
\(\overline{GF}\) نیمساز \(\overline{AE}\) می باشد
تعریف تنصیف.
-
\(\overline{GF} \bot \overline{AE}\)
اگر یک شعاع یک وتر را تنصیف کند (و آن وتر قطر نباشد)، آن گاه بر روی آن وتر عمود می باشد.
-
\(\angle{AFG}\) و \(\angle{EFG}\) زوایای قائمه می باشند
تعریف خطوط متعامد.
-
\(\angle{AFG} \cong \angle{EFG}\)
تمامی زوایای قائمه با یکدیگر همنهشتند.
-
\(\overline{CF} \cong \overline{CF}\)
خاصیت بازتابی.
-
\(\triangle{AFC} \cong \triangle{CFC}\)
اصل SAS (گزاره های 2، 6، و 7).
-
\(\overline{AC} \cong \overline{EC}\)
CPCTC
-
\(\overline{GB} \cong \overline{GD}\)
اگر دو وتر از یک دایره همنهشت باشند، آن گاه از مرکز آن دایره فاصلۀ یکسانی دارند (متساوی الفاصله می باشند).
-
\(\overline{GB}\) نیمساز \(\overline{AC}\) می باشد
\(\overline{GD}\) نیمساز \(\overline{EC}\) می باشد
اگر یک شعاع بر یک وتر عمود باشد، سپس آن وتر را تنصیف می کند.
-
\(\overline{CB} \cong \overline{CD}\)
تقسیمات مشابه (گزاره های 9 و 11).
-
\(BCDG\) یک کایت می باشد
تعریف کایت (دو جفت جدا از هم از اضلاع متوالی همنهشت می باشند، گزاره های 10 و 12).
استفاده از شعاع های اضافی برای حل یک مسأله
در هنگام حل کردن مسأله های دایره، سه چیز مهم می باشد، شعاع، شعاع، و باز هم شعاع! دلیل اینگونه مطرح کردن تاکید بر روی اهمیت شعاع می باشد. بسیار مهم است که به تمامی شعاع ها در یک مسألۀ دایره توجه کنید و بررسی کنید که در کجاهای شکل هندسی مسأله می توانید شعاع های دیگری را بیفزایید. معمولاً به اضافه کردن شعاع ها نیاز دارید تا مثلث های قائم الزاویه یا متساوی الساقین را بسازید تا از آنها برای حل مسأله استفاده کنید. کاری که انجام می دهید همراه با جزئیات بیشتر در اینجا آمده است:
-
شعاع های اضافی را بر روی شکل ترسیم کنید.
شما باید شعاع ها را، درست به جایِ هر نقطۀ دیگری بر روی دایره ترسیم کنید تا به جایی اشاره کنند که چیز دیگری با دایره تقاطع دارد یا اینکه آن را لمس کرده است.
-
چشمانتان را باز کنید و به تمامی شعاع ها توجه کنید ـــ شامل شعاع های جدیدی که خودتان ترسیم نموده اید ـــ و تمامی آنها را به عنوان همنهشت علامت بزنید.
به برخی دلایل ـــ با وجود اینکه همنهشت بودن تمامی شعاع ها، یکی از ساده ترین قضایای هندسه می باشد ـــ افراد مکرراً یا در تشخیص تمامی شعاع ها در یک مسأله قصور می ورزند و یا اینکه در توجه به اینکه آنها همنهشت می باشند دچار اشتباه می گردند.
-
پاره خطی (بخشی از یک شعاع) را ترسیم کنید که از مرکز یک دایره به یک وتر می رسد و بر آن وتر عمود می باشد.
این پاره خط آن وتر را تنصیف می کند (من این قضیه را در بخش پیشین مورد اشاره قرار دادم).
اکنون این مسأله را بررسی کنید: مساحت چهارضلعی محاط شدۀ \(GHJK\) که در شکل سمت چپ نشان داده شده است را بیابید. این دایره دارای شعاع \(2\) می باشد.
در اینجا نکته ای داریم که منجر می شود، دو راهنمایی به شما ارائه شود. اولین راهنما اینکه همانطور که در شکل سمت راست می بینید، چهار شعاع را به چهار رأس این چهارضلعی ترسیم کنید.

اکنون به سادگی فقط نیاز دارید تا مساحت هر مثلث را به صورت جداگانه بیابید. شما می توانید ببینید که \(\triangle{JKC}\) متوازی الاضلاع می باشد، بنابراین می توانید از فرمول مساحت مثلث متوازی الاضلاع برای آن استفاده کنید (این فرمول در فصل 7 ارائه شده است):
$$Area_{\triangle{JKC}} = \frac{s^2\sqrt{3}}{4}= \frac{2^2\sqrt{3}}{4}=\sqrt{3} \text{ units}^2$$
و اگر حواستان جمع باشد، باید مثلثهای \(GHC\) و \(HJC\) را شناسایی کرده باشید. اضلاع آنها در نسبت \(2:2:2\sqrt{2}\) می باشند، که به \(1:1:\sqrt{2}\) کاهش می یابد؛ از این رو، آنها مثلثهای \(45^{\circ}-45^{\circ}-90^{\circ}\) می باشند (فصل 8 را ببینید). شما هم اکنون قاعده و ارتفاع این مثلث ها را می دانید، بنابراین رسیدن به مساحت آنها به سادگیِ یک بشکن زدن می باشد. برای هر کدام از این مثلثها داریم:
$$Area=\frac{1}{2}bh=\frac{1}{2} \cdot 2 \cdot 2 = 2 \text{ units}^2$$
راهنمای دیگری که می تواند به شما کمک کند در ارتباط با \(\triangle{KGC}\) می باشد. ارتفاع آن را ترسیم کنید، برای ترسیم ارتفاع بخشی از شعاع آن را از مرکز دایره، یعنی \(C\)، به \(\overline{GK}\) ترسیم کنید. این شعاع بر \(\overline{GK}\) عمود می باشد و از این رو \(\overline{GK}\) را به دو پاره خط برابر با طول \(\sqrt{3}\) تقسیم می کند. شما \(\triangle{KGC}\) را به دو مثلث قائم الزاویه تقسیم کرده اید؛ هر کدام از این مثلثها دارای وتر \(2\) و یک ساق با اندازۀ \(\sqrt{3}\) می باشند، بنابراین اندازۀ ساق دیگر (ارتفاع) برابر با \(1\) می باشد (اندازۀ این ساق را با استفاده از قضیۀ فیثاغورث و یا با شناسایی نسبت این مثلث که \(1:\sqrt{3}:2\) می باشد و در واقع یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) است، بدست می آورید). بنابراین \(\triangle{KGC}\) دارای ارتفاع \(1\) و قاعدۀ \(2\sqrt{3}\) می باشد. کافیست این مقادیر را در فرمول معمولی مساحت مثلث جایگذاری کنید:
$$Area_{\triangle{KGC}}=\frac{1}{2}bh=\frac{1}{2} \cdot 2\sqrt{3} \cdot 1 = \sqrt{3} \text{ units}^2$$
اکنون برای محاسبۀ مساحت چهارضلعی، مساحت این مثلث ها را با یکدیگر جمع می زنیم:
$$
\text{Area}_{GHIJ} = \text{area}_{\triangle{JKC}} + \text{area}_{\triangle{GHC}} + \text{area}_{\triangle{HJC}} + \text{area}_{\triangle{KGC}} \\
= \sqrt{3}+2+2+\sqrt{3} \\
= 4+2\sqrt{3} \approx 7.46 \text{ units}^2
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: