خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
قطعۀ دایره، قطاع دایره، و مساحت آنها

دانش آموزان معمولاً این سوال را می پرسند، "چه وقتی قرار است تا از این استفاده کنم؟"، خوب، من گمان می کنم که این کتاب شامل بسیاری از چیزها می باشد که به این زودی ها از آنها استفاده نخواهید کرد، اما یک چیز را با اطمینان می دانم و آن اینست که چیزهای مربوط به شکلهای مدور را هزاران بار در زندگی تان استفاده خواهید کرد. هر بار که در خودرویتان مشغول رانندگی هستید، با چهار لاستیک، فرمان مدور، دکمۀ گردان صدای ضبط صوت، دکمۀ گردان تهویۀ خودرو، چرخ دنده ها، دریچۀ کوچکی که از آنجا تایرها را باد می زنید که البته اسمش را فراموش کرده ام، و به همین ترتیب. و تمامی اختراعات و محصولاتی که از این شکل فراگیر استفاده کرده اند را نیز در نظر بگیرید: چرخ و فلک ها، ژیروسکوپ ها (چرخش نما ها)، لنزها، دریچۀ گرد فاضلاب ها، لوله ها، چرخ آسیاب آبی، و چیزهای خیلی خیلی بیشتر.

در این فصل، چیزهای شگفت انگیزی را در مورد دایره کشف خواهید کرد. فرمول ها و قضایای بسیاری را در مورد دایره ها و ارتباط بین دایره ها، زوایا، کمان ها، و قطعات مختلف مربوط به دایره ها (وترها، مماس ها، و خطهای قاطع) را بررسی خواهید کرد. در اکثر موارد، این فرمولها شامل روشی می باشند که این اشیاء هندسی یکدیگر را برش می دهند یا تقسیم می کنند: دایره ها خط های قاطع را جدا می کنند، زوایا، کمان ها را از دایره ها جدا می کنند، وترها، وترها را جدا می کنند، و به همین ترتیب.
در این بخش، شما با دو فرمول پایه ای آغاز می کنید: فرمول های مساحت و محیط یک دایره. سپس از این فرمولها استفاده می کنید تا طول، محیط، و مساحت بخشهای مختلف یک دایره را محاسبه کنید: کمان ها (arcs)، قطاع ها (sectors) ، و قطعه ها (segments).
برای اطلاعات بیشتر در مورد طول کمان و مساحت قطاع ها و قطعه ها، ادامۀ این فصل را بخوانید. اگر بتوانید دلایل سادۀ پشت این فرمولها را درک کنید، قادر خواهید بود تا مسأله های کمان، قطاع، و قطعه را حتی با وجود فراموش کردن فرمولهایشان، حل کنید.
قبل از اینکه وارد فرمول طول کمان شوید، می خواهم به یکی از دلایل بالقوۀ به اشتباه افتادن در مورد کمان ها و چگونگی اندازه گیری آنها اشاره کنم. در فصل 14، اندازۀ یک کمان بر اساس واحد درجۀ زاویۀ مرکزی که آن کمان را بریده است، تعریف شده است. وقتی می گوییم اندازۀ یک کمان \(60^{\circ}\) می باشد، به سادگی منظور اینست که زاویۀ مرکزی مرتبط با آن یک زاویۀ \(60^{\circ}\) می باشد. اما اکنون، در این بخش، چگونگی تعیین طول یک کمان را بررسی می کنیم. طول یک کمان همان چیز رایجی در مورد طول است که منظور همیشگی شماست ـــ مانند طول یک رشته نخ (البته، در مورد کمان ها، یک نخ خمیده منظور است). به طور خلاصه، اندازۀ یک کمان، اندازۀ زاویۀ مرکزی آن بر حسب درجه می باشد؛ و طول یک کمان، همان طول عادی امتداد آن کمان می باشد.
دور تا دور یک دایره برابر با \(360^{\circ}\) می باشد؛ از اینرو، اگر اندازۀ درجۀ یک کمان را بر \(360^{\circ}\) تقسیم کنید، کسری از محیط دایره که آن کمان می سازد را پیدا خواهید کرد.
آن گاه، اگر طول دور تا دور آن دایره (محیط دایره) را در آن کسر ضرب کنید، به طول آن کمان می رسید. خوب، سرانجام، فرمولی که منتظرش بودید اینجاست.
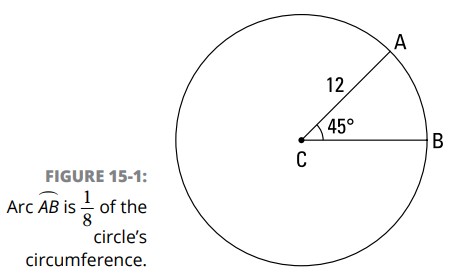
محاسبۀ مربوط به \(\overparen{AB}\) را بررسی کنید. اندازۀ درجۀ آن \(45^{\circ}\) و شعاع این دایره \(12\) می باشد، بنابراین طول این کمان اینگونه بدست می آید:
$$
\text{Length}_{\overparen{AB}}=\biggl( \frac{m\overparen{AB}}{360} \biggr) (2 \pi r) \\
= \frac{45}{360} \cdot 2 \cdot \pi \cdot 12 \\
=\frac{1}{8} \cdot 24 \pi \\
= 3 \pi \approx 9.42 \text{ units}
$$
همانطور که می بینید، از آنجا که \(45^{\circ}\) برابر با \(\frac{1}{8}\) از \(360^{\circ}\) است، طول کمان \(\overparen{AB}\) برابر با \(\frac{1}{8}\) محیط این دایره می باشد. بسیار ساده است، اینطور نیست؟
بله، درست خواندید. شما می توانید مساحت یک قطعه (segment) در دایره را بیابید. نه، البته که منظور مساحت یک پاره خط (line segment) نمی باشد (پاره خط مساحت ندارد)، منظور مساحت یک قطعه از دایره (segment of a circle) می باشد ـــ این دو چیز کاملاً متفاوت می باشند. یک قطعه در دایره، تکه ای از یک دایره می باشد که توسط یک وتر و یک کمان محاصره شده است. ناحیه دیگری بر روی دایره که در اینجا مورد بررسی قرار خواهیم داد، قطاع (sector) می باشد ـــ یک تکه از یک دایره که توسط دو شعاع و یک کمان محصور شده است. در این بخش، چگونگی یافتن مساحت هر کدام از این نواحی را به شما نشان خواهم داد.

درست شبیه یک کمان که بخشی از محیط یک دایره می باشد، یک قطاع بخشی از مساحت یک دایره می باشد؛ از این رو، محاسبۀ مساحت یک قطاع مشابه فرمول طول کمان که در بخش پیشین اشاره شد، عمل می کند.
با استفاده از این فرمول، مساحت قطاع \(ACB\) در شکل 1-15 را بیابید:
$$
\text{Area}_{\text{Sector }ACB}=\biggl( \frac{m\overparen{AB}}{360} \biggr) (\pi r^2) \\
=\frac{1}{8} \cdot \pi \cdot 12^2 \\
= 18 \pi \approx 56.55 \text{ units}^2
$$
از آنجا که \(45^{\circ}\) برابر با \(\frac{1}{8}\) از \(360^{\circ}\) می باشد، مساحت قطاع \(ACB\) برابر با \(\frac{1}{8}\) مساحت این دایره می باشد (درست همانند طول \(\overparen{AB}\) که برابر با \(\frac{1}{8}\) از محیط این دایره است).
شما می دانید که چگونه مساحت یک قطاع را محاسبه کنید. برای بدست آوردنِ مساحت این مثلث، یک ارتفاع ترسیم می کنید که از مرکز دایره به وتری که قاعدۀ این مثلث را می سازد می رود. سپس این ارتفاع ساقی از یک مثلث قائم الزاویه می گردد که وتر آن شعاعی از این دایره می باشد. شما با مفاهیم مثلث قائم الزاویه همچون قضیۀ فیثاغورث کار را تمام می کنید. در بخش بعدی چگونگی انجام تمامی این کارها را همراه با جزئیاتشان به شما نشان می دهم.
مسألۀ زیر، یافتن طول کمان، مساحت قطاع، و مساحت قطعه را نشان می دهد:
داده ها:
دایرۀ \(D\) با شعاع \(6\)
پیدا کنید:
در اینجا پاسخ این مسألۀ سه بخشی را می بینید:

در این فصل، چیزهای شگفت انگیزی را در مورد دایره کشف خواهید کرد. فرمول ها و قضایای بسیاری را در مورد دایره ها و ارتباط بین دایره ها، زوایا، کمان ها، و قطعات مختلف مربوط به دایره ها (وترها، مماس ها، و خطهای قاطع) را بررسی خواهید کرد. در اکثر موارد، این فرمولها شامل روشی می باشند که این اشیاء هندسی یکدیگر را برش می دهند یا تقسیم می کنند: دایره ها خط های قاطع را جدا می کنند، زوایا، کمان ها را از دایره ها جدا می کنند، وترها، وترها را جدا می کنند، و به همین ترتیب.
محیط و مساحت دایره
در این بخش، شما با دو فرمول پایه ای آغاز می کنید: فرمول های مساحت و محیط یک دایره. سپس از این فرمولها استفاده می کنید تا طول، محیط، و مساحت بخشهای مختلف یک دایره را محاسبه کنید: کمان ها (arcs)، قطاع ها (sectors) ، و قطعه ها (segments).
محیط (Circumference) و مساحت (area) یک دایره: علاوه بر قضیۀ فیثاغورث و چند فرمول دیگر، دو فرمول دایرۀ زیر در زمرۀ شناخته شده ترین فرمول ها در هندسه می باشند. در این فرمول ها، \(r\) شعاع (radius) دایره، و \(d\) قطر (diameter) آن می باشند:
-
\(\text{Circumference} = 2 \pi r\) یا \(\text{Circumference} = \pi d\)
-
\(\text{Area}_{\text{Circle}}= \pi r^2\)
برای اطلاعات بیشتر در مورد طول کمان و مساحت قطاع ها و قطعه ها، ادامۀ این فصل را بخوانید. اگر بتوانید دلایل سادۀ پشت این فرمولها را درک کنید، قادر خواهید بود تا مسأله های کمان، قطاع، و قطعه را حتی با وجود فراموش کردن فرمولهایشان، حل کنید.
تعیین طول کمان
قبل از اینکه وارد فرمول طول کمان شوید، می خواهم به یکی از دلایل بالقوۀ به اشتباه افتادن در مورد کمان ها و چگونگی اندازه گیری آنها اشاره کنم. در فصل 14، اندازۀ یک کمان بر اساس واحد درجۀ زاویۀ مرکزی که آن کمان را بریده است، تعریف شده است. وقتی می گوییم اندازۀ یک کمان \(60^{\circ}\) می باشد، به سادگی منظور اینست که زاویۀ مرکزی مرتبط با آن یک زاویۀ \(60^{\circ}\) می باشد. اما اکنون، در این بخش، چگونگی تعیین طول یک کمان را بررسی می کنیم. طول یک کمان همان چیز رایجی در مورد طول است که منظور همیشگی شماست ـــ مانند طول یک رشته نخ (البته، در مورد کمان ها، یک نخ خمیده منظور است). به طور خلاصه، اندازۀ یک کمان، اندازۀ زاویۀ مرکزی آن بر حسب درجه می باشد؛ و طول یک کمان، همان طول عادی امتداد آن کمان می باشد.
دور تا دور یک دایره برابر با \(360^{\circ}\) می باشد؛ از اینرو، اگر اندازۀ درجۀ یک کمان را بر \(360^{\circ}\) تقسیم کنید، کسری از محیط دایره که آن کمان می سازد را پیدا خواهید کرد.
آن گاه، اگر طول دور تا دور آن دایره (محیط دایره) را در آن کسر ضرب کنید، به طول آن کمان می رسید. خوب، سرانجام، فرمولی که منتظرش بودید اینجاست.
طول کمان (Arc length): طول یک کمان (بخشی از محیط دایره، مانند \(\overparen{AB}\) در شکل 1-15) برابر است با محیط آن دایره (\(2\pi r\)) ضربدر کسری از آن دایره که با اندازۀ آن کمان نشان داده می شود (توجه داشته باشید که اندازۀ درجۀ یک کمان به شکل \(m\overparen{AB}\) نوشته می شود):
$$
\text{Length}_{\overparen{AB}} = \biggl(\frac{m\overparen{AB}}{360}\biggr) (2 \pi r)
$$
$$
\text{Length}_{\overparen{AB}} = \biggl(\frac{m\overparen{AB}}{360}\biggr) (2 \pi r)
$$

محاسبۀ مربوط به \(\overparen{AB}\) را بررسی کنید. اندازۀ درجۀ آن \(45^{\circ}\) و شعاع این دایره \(12\) می باشد، بنابراین طول این کمان اینگونه بدست می آید:
$$
\text{Length}_{\overparen{AB}}=\biggl( \frac{m\overparen{AB}}{360} \biggr) (2 \pi r) \\
= \frac{45}{360} \cdot 2 \cdot \pi \cdot 12 \\
=\frac{1}{8} \cdot 24 \pi \\
= 3 \pi \approx 9.42 \text{ units}
$$
همانطور که می بینید، از آنجا که \(45^{\circ}\) برابر با \(\frac{1}{8}\) از \(360^{\circ}\) است، طول کمان \(\overparen{AB}\) برابر با \(\frac{1}{8}\) محیط این دایره می باشد. بسیار ساده است، اینطور نیست؟
محاسبۀ مساحت قطاع و قطعه در دایره
بله، درست خواندید. شما می توانید مساحت یک قطعه (segment) در دایره را بیابید. نه، البته که منظور مساحت یک پاره خط (line segment) نمی باشد (پاره خط مساحت ندارد)، منظور مساحت یک قطعه از دایره (segment of a circle) می باشد ـــ این دو چیز کاملاً متفاوت می باشند. یک قطعه در دایره، تکه ای از یک دایره می باشد که توسط یک وتر و یک کمان محاصره شده است. ناحیه دیگری بر روی دایره که در اینجا مورد بررسی قرار خواهیم داد، قطاع (sector) می باشد ـــ یک تکه از یک دایره که توسط دو شعاع و یک کمان محصور شده است. در این بخش، چگونگی یافتن مساحت هر کدام از این نواحی را به شما نشان خواهم داد.
در اینجا تعاریف این دو ناحیه را داریم (شکل 2-15 هر دوی اینها را به شما نشان می دهد):
-
قطاع (Sector): یک ناحیه از دایره که توسط دو شعاع و یک کمان محدود شده است (به زبان ساده تر: شکل یک تکه از پیتزا).
-
قطعۀ دایره (Segment of a circle): یک ناحیه در دایره که توسط یک وتر و یک کمان محدود شده است ـــ به آن مقطع نیز گفته می شود.

درست شبیه یک کمان که بخشی از محیط یک دایره می باشد، یک قطاع بخشی از مساحت یک دایره می باشد؛ از این رو، محاسبۀ مساحت یک قطاع مشابه فرمول طول کمان که در بخش پیشین اشاره شد، عمل می کند.
مساحت یک قطاع (Area of a sector): مساحت یک قطاع (مانند قطاع \(PQR\) در شکل 2-15) برابر است با مساحت آن دایره (\(\pi r^2\)) ضربدر کسری از آن دایره که توسط این قطاع نشان داده شده است:
$$ \text{Area}_{\text{Sector PQR}} = \biggl( \frac{m \overparen{PR}}{360} \biggr) (\pi r^2) $$
$$ \text{Area}_{\text{Sector PQR}} = \biggl( \frac{m \overparen{PR}}{360} \biggr) (\pi r^2) $$
با استفاده از این فرمول، مساحت قطاع \(ACB\) در شکل 1-15 را بیابید:
$$
\text{Area}_{\text{Sector }ACB}=\biggl( \frac{m\overparen{AB}}{360} \biggr) (\pi r^2) \\
=\frac{1}{8} \cdot \pi \cdot 12^2 \\
= 18 \pi \approx 56.55 \text{ units}^2
$$
از آنجا که \(45^{\circ}\) برابر با \(\frac{1}{8}\) از \(360^{\circ}\) می باشد، مساحت قطاع \(ACB\) برابر با \(\frac{1}{8}\) مساحت این دایره می باشد (درست همانند طول \(\overparen{AB}\) که برابر با \(\frac{1}{8}\) از محیط این دایره است).
مساحت یک قطعۀ دایره (Area of a segment): برای یافتن مساحت یک قطعه، مانند قطعه ای که در شکل 2-15 می بینید، کافیست مساحت آن مثلث را از مساحت آن قطاع تفریق کنید (ضمناً، هیچ روش فنی برای نامگذاری قطعه ها وجود ندارد، اما بیایید این یکی را قطعۀ \(XZ\) بنامیم):
$$\text{Area}_{\text{Circle Segment }XZ}=\text{area}_{\text{Sector }XYZ} - \text{area}_{\triangle{XYZ}}$$
$$\text{Area}_{\text{Circle Segment }XZ}=\text{area}_{\text{Sector }XYZ} - \text{area}_{\triangle{XYZ}}$$
شما می دانید که چگونه مساحت یک قطاع را محاسبه کنید. برای بدست آوردنِ مساحت این مثلث، یک ارتفاع ترسیم می کنید که از مرکز دایره به وتری که قاعدۀ این مثلث را می سازد می رود. سپس این ارتفاع ساقی از یک مثلث قائم الزاویه می گردد که وتر آن شعاعی از این دایره می باشد. شما با مفاهیم مثلث قائم الزاویه همچون قضیۀ فیثاغورث کار را تمام می کنید. در بخش بعدی چگونگی انجام تمامی این کارها را همراه با جزئیاتشان به شما نشان می دهم.
مسأله ترکیبی از طول کمان، مساحت قطاع، و مساحت قطعه
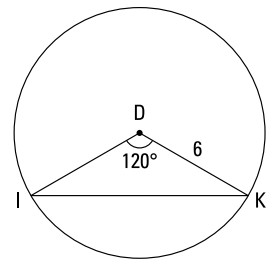
مسألۀ زیر، یافتن طول کمان، مساحت قطاع، و مساحت قطعه را نشان می دهد:

داده ها:
دایرۀ \(D\) با شعاع \(6\)
پیدا کنید:
-
طول کمان \(\overparen{IK}\)
-
مساحت قطاع \(IDK\)
-
مساحت قطعه دایرۀ \(IK\)
در اینجا پاسخ این مسألۀ سه بخشی را می بینید:
-
طول کمان \(\overparen{IK}\) را بیابید.
اگر مفاهیم را به درستی درک کرده باشید، برای یافتن طول کمان، نیازی به فرمول ندارید: اندازۀ این کمان \(120^{\circ}\) می باشد، که یک سوم \(360^{\circ}\) است، بنابراین طول \(\overparen{IK}\) برابر با یک سوم محیط دایرۀ \(D\) می باشد. همه اش همین بود. در اینجا چگونگی این کار را با جایگزینی مقادیر در فرمول محاسبۀ طول کمان می بینید:
$$
\text{Length}_{\overparen{IK}}=\biggl( \frac{m\overparen{IK}}{360} \biggr) (2 \pi r) \\
=\frac{120}{360} \cdot 12 \pi \\
=\frac{1}{3} \cdot 12 \pi \\
= 4 \pi \approx 12.6 \text{ units}
$$
-
مساحت قطاع \(IDK\) را بیابید.
یک قطاع بخشی از مساحت یک دایره می باشد. از آنجا که \(120^{\circ}\) یک سوم مساحت یک دایره را می گیرد، قطاع \(IDK\) یک سوم مساحت این دایره را اشغال می کند. در اینجا پاسخ رسمی را می بینید:
$$
\text{Area}_{\text{Sector }IDK} = \biggl( \frac{m\overparen{IK}}{360} \biggr) (\pi r^2) \\
= \frac{120}{360} \cdot 36 \pi \\
=\frac{1}{3} \cdot 36 \pi \\
= 12 \pi \approx 37.7 \text{ units}^2
$$
-
مساحت قطعه دایرۀ \(IK\) را بیابید.
برای یافتن مساحت قطعه، نیاز به مساحت \(\triangle{IDK}\) دارید تا بتوانید آنرا از مساحت قطاع \(IDK\) تفریق کنید. یک ارتفاع را مستقیماً از \(D\) با \(\overline{IK}\) ترسیم کنید. این کار منجر می شود تا دو مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) ایجاد گردد. اندازۀ اضلاع یک مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) در نسبت \(x:x\sqrt{3}:2x\) می باشند (فصل 8 را ببینید)، که در آن \(x\) ساق کوتاهتر، \(x\sqrt{3}\) ساق بزرگتر، و \(2x\) وتر می باشند. در این مسأله، وتر برابر با \(6\) می باشد، بنابراین ارتفاع (ساق کوتاهتر) نصفِ آن ، یعنی \(3\)، می باشد، و قاعده (ساق بلندتر) برابر با \(3\sqrt{3}\) است. \(\overline{IK}\) دو برابر قاعدۀ مثلث \(30^{\circ}-60^{\circ}-90^{\circ}\) است، بنابراین دو برابر \(3\sqrt{3}\)، یا \(6\sqrt{3}\) است. شما آماده هستید تا این مسأله را با فرمول مساحت قطعه به پایان برسانید:
$$
\text{Area}_{\text{Segment} IDK}=\text{area}_{\text{Sector }IDK} = \text{area}_{\triangle{IDK}} \\
= 12 \pi - \frac{1}{2}bh \\
=12 \pi - \frac{1}{2} \cdot 6\sqrt{3} \cdot 3 \\
= 12 \pi - 9\sqrt{3} \\
\approx 22.1 \text{ units}^2
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: