انواع زوایا در دایره

در این بخش، زوایایی که یک دایره را قطع می کنند، بررسی می کنیم. رأس های این زوایا می توانند درون دایره باشند، روی دایره باشند، یا بیرون دایره باشند. فرمولهای موجود در این بخش به شما می گویند این زوایا چگونه با کمان هایی که جدا کرده اند، مرتبط می باشند. همانند بسیاری دیگر از موضوعات ارائه شده در این کتاب، ارشمیدس (Archimedes) و سایر ریاضیدانان از حدود دو هزاره قبل این ارتباطات بین کمان ها و زوایا را می دانسته اند.

زوایای روی محیط یک دایره

از سه مکانی که رأس های یک زاویه می تواند با دایره در ارتباط باشد، زوایایی که رأس های آنها بر روی محیط یک دایره قرار می گیرند مواردی هستند که در بیشتر مسأله ها می آیند و از اینرو مهمترین آنها می باشند. این زوایا در دو نوع مختلف وجود دارند:

زاویۀ محاطی (Inscribed angle): یک زاویۀ محاطی، مانند $\angle{BCD}$ در بخش a از شکل 3-15 ، زاویه ای است که رأس آن روی محیط دایره قرار گرفته است و اضلاع آن دو وتر از آن دایره می باشند.
زاویۀ تانژانت-وتر (Tangent-chord angle) که با نام زاویۀ ظلی شناخته می شود: یک زاویۀ ظلی، همانند $\angle{JKL}$ ، در بخش b از شکل 3-15، زاویه ای است که رأس آن روی محیط یک دایره قرار گرفته است و اضلاع آن یک تانژانت و یک وتر از آن دایره می باشند (برای اطلاعات بیشتر در مورد تانژانت و وتر فصل 14 را ببینید).

اندازۀ یک زاویۀ قرار گرفته بر روی محیط دایره (Measure of an angle on a circle): اندازۀ یک زاویۀ محاطی یا یک زاویۀ ظلی (زاویۀ تانژانت-وتر) برابر با نصفِ اندازه کمانی است که آن زاویه جدا کرده است.

به عنوان مثال، در شکل 3-15 ، $\angle{BCD}=\frac{1}{2}\bigl( m\overparen{BD} \bigr)$ و $\angle{JKL}=\frac{1}{2}\biggl( m\overparen{JK} \biggr)$ .

مطمئن شوید که این مفهوم ساده را به حافظه سپرده باشید که یک زاویه بر روی محیط یک دایره، نصفِ اندازۀ کمانی است که جدا کرده است (یا، اگر از سمت مقابلش به آن بنگرید، اندازۀ این کمان دوبرابر اندازۀ زاویه اش می باشد). اگر یادتان رفت کدام نصفِ کدام است، این را امتحان کنید: یک شکل سریع از یک دایره همراه با یک کمان $90^{\circ}$ (یک چهارم دایره) بکشید و یک زاویۀ محاطی که آن کمان $90^{\circ}$ را جدا کرده باشد رسم کنید. شما فوراً متوجه خواهید شد که این زاویه کوچکتر از $90^{\circ}$ می باشد، که به شما نشان می دهد آن زاویه چیزی است که نصفِ کمان می باشد، و نه برعکس آن.

زوایای همنهشت روی محیط یک دایره (Congruent angles on a circle): قضایای زیر در مورد موقعیت هایی به شما می گویند که در آنها شما دو زاویۀ همنهشت را بر روی یک دایره بدست می آورید:

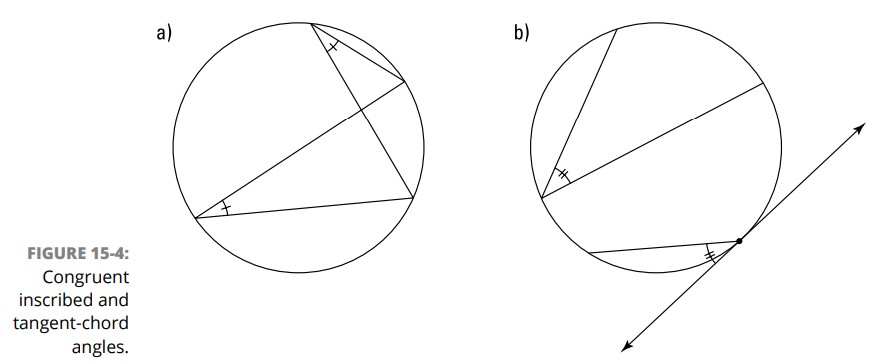
اگر دو زاویۀ محاطی یا دو زاویۀ ظلی (تانژانت-وتر)، کمان یکسانی را جدا کنند، آن گاه آن زوایا با هم همنهشت می باشند (بخش a از شکل 4-15 را ببینید).
اگر دو زاویۀ محاطی یا دو زاویۀ ظلی (تانژانت-وتر)، کمان های همنهشتی را جدا کنند، آن گاه آن زوایا با هم همنهشت می باشند (بخش b از شکل 4-15 را ببینید).

زمان آن فرا رسیده است تا این مفاهیم را در عمل ببینیم ـــ نگاهی به مسأله زیر بیندازید:

داده ها:
شکل هندسی به نحویکه می بینید
$\angle{QPS} = 75^{\circ}$
پیدا کنید:
زوایای $1$، $2$، $3$، و $4$ و اندازۀ کمان های $\overparen{SP}$ ، $\overparen{PQ}$، و $\overparen{QR}$

در اینجا چگونگی حل این مسأله را می بینید. کافیست استفاده از فرمول زاویه محاطی را دوباره و دوباره ادامه بدهید. یادتان باشد ـــ زاویه نصفِ کمان می باشد؛ کمان دوبرابر زاویه می باشد.

$\overparen{SP}$ دو برابر زاویۀ $60^{\circ}$ می باشد، پس برابر با $120^{\circ}$ است. زاویۀ $2$ نصف آن است، پس برابر با $60^{\circ}$ است (یا با استفاده از اولین قضیۀ زوایای همنهشت در این بخش داریم، $\angle{2}$ باید با $\angle{PRS}$ برابر باشد زیرا هر دوی آنها کمان یکسانی را جدا می کنند).

$\overparen{RS}$ برابر با $40^{\circ}$ است، پس $\angle{RPS}$ نصف آن، یعنی $20^{\circ}$ می شود. تفریق آن از $\angle{QPS}$ (که در داده ها گفته شده برابر با $75^{\circ}$ است) به شما مقدار $55^{\circ}$ را برای $\angle{1}$ می دهد. $\overparen{QR}$ دو برابر آن ($110^{\circ}$) می باشد؛ و از آنجا که $\angle{3}$ ، $\overparen{QR}$ را جدا می کند، نصف آن، یعنی $55^{\circ}$ است. (دوباره، شما می توانستید متوجه شوید $\angle{3}$ و $\angle{1}$ برابر می باشند، زیرا هر دوی آنها $\overparen{QR}$ را جدا می کنند.)

اکنون اندازۀ $\overparen{PQ}$ را بدست آورید. چهار کمان ـــ $\overparen{QR}$ ، $\overparen{RS}$ ، $\overparen{SP}$ ، و $\overparen{PQ}$ ـــ کل این دایره را تشکیل می دهند، که $360^{\circ}$ می باشد. شما اندازۀ سه کمان اول را دارید: به ترتیب $110^{\circ}$ ، $40^{\circ}$ ، و $120^{\circ}$ . مجموع آنها $270^{\circ}$ می شود. از اینرو، $\overparen{PQ}$ برابر با $360^{\circ}-270^{\circ}$ یا $90^{\circ}$ می باشد. در پایان، $\angle{4}$ نصف آن، یعنی $45^{\circ}$ است. (شما همچنین می توانستید مقدار $\angle{4}$ را با استفاده از این حقیقت که مجموع زوایای $\triangle{PRS}$ باید $180^{\circ}$ گردد، بدست آورید. صرفاً اندازه زوایای $\angle{R}$ ، $\angle{RPS}$ ، و $\angle{3}$ را با هم جمع بزنید، و حاصل را از $180^{\circ}$ تفریق کنید.)

نکته: این ایدۀ مثلث، همچنین روش خوبی را به شما می دهد تا نتایج را درست آزمایی کنید (فرض کنیم اندازۀ $\angle{4}$ را با روش اول بدست آورده اید). زاویۀ $R$ برابر با $60^{\circ}$ ، $\angle{RPS}$ برابر با $20^{\circ}$ ، $\angle{3}$ برابر با $55^{\circ}$ ، و $\angle{4}$ برابر با $45^{\circ}$ می باشند. مجموع اینها برابر با $180^{\circ}$ است، بنابراین پاسخ ها درست آزمایی می گردند، و منجر می شود تا نکته بعدی را به شما بگویم.

هرگاه که میسر باشد، پاسخهایتان را با روشی که متفاوت از روش مورد استفاده قرار گرفته در حل مسأله می باشد، درست آزمایی کنید. این کار نسبت به مرور مجدد مراحل حل مسأله برای بار دوم بسیار کارآمدتر می باشد و اشتباهات احتمالی را راحتتر به دام می اندازید.

زوایای داخل یک دایره

در این بخش، در مورد زوایای بحث خواهم کرد که رأس های آنها درون دایره قرار دارد اما دایره را لمس نمی کند.

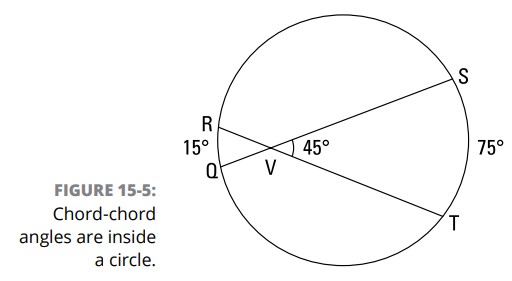
اندازۀ یک زاویه درون دایره (Measure of an angle inside a circle): اندازه یک زاویه که رأس آن درون یک دایره قرار دارد (یک زاویۀ وتر-وتر)، یک دوم مجموع اندازۀ کمان هایی می باشد که توسط آن زاویه و زاویۀ متقابل به رأس آن جدا شده اند. به عنوان مثال، شکل 5-15 را بررسی کنید، که زاویۀ وتر-وتر (chord-chord angle) $SVT$ را به شما نشان می دهد. شما اندازۀ این زاویه را اینگونه پیدا می کنید:
$$\angle{SVT} = \frac{1}{2} \biggl( m\overparen{ST}+m\overparen{QR} \biggr)$$

یادداشت مترجم: به زوایایی که رأس آنها داخل دایره قرار گرفته باشد، زاویۀ بین دو وتر یا زاویۀ داخلی دایره نیز گفته می شود.

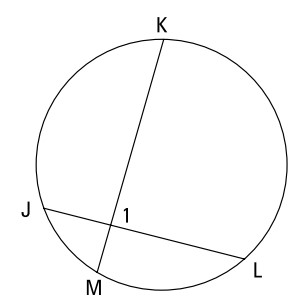
در اینجا یک مسأله داریم که چگونگی اجرای این فرمول را به شما نشان می دهد:

داده ها:
$\overparen{MJ}:\overparen{JK}:\overparen{KL}:\overparen{LM}=1:3:4:2$
پیدا کنید:
$\angle{1}$

برای استفاده از این فرمول جهت یافتن $\angle{1}$ ، شما به اندازۀ کمان های $MJ$ و $KL$ نیاز دارید. شما می دانید که نسبت کمان های $MJ$ ، $JK$ ، $KL$ ، و $LM$ برابر است با $1:3:4:2$ می باشد، بنابراین می توانید اندازۀ آنها را برابر با $1x$ ، $3x$ ، $4x$ ، و $2x$ قرار دهید. این چهار کمان یک دایرۀ کامل را می سازند، بنابراین حاصلجمع آنها باید برابر با $360^{\circ}$ باشد. از اینرو:
$$1x+3x+4x+2x=360 \\
10x=360 \\
x=36$$
عدد $36$ را جایگزین $x$ کنید تا اندازۀ $\overparen{MJ}$ و $\overparen{KL}$ را بیابید:
$$
m\overparen{MJ}=1x=36^{\circ} \\
m\overparen{KL}=4x=4 \cdot 36 = 144^{\circ}
$$
اکنون از این فرمول استفاده کنید:
$$
\angle{1}=\frac{1}{2}\biggl( m\overparen{KL}+m\overparen{MJ} \biggr) \\
=\frac{1}{2}(144+36) \\
=\frac{1}{2}(180) \\
=90^{\circ}
$$
تمام شد. پنج دقیقه به خودتان استراحت بدهید.

زوایای بیرون یک دایره

در بخشهای پیشین، زوایایی را بررسی کردیم که رأس های آنها روی محیط دایره و درون یک دایره قرار داشتند. تنها یک محل دیگر برای قرارگیری رأس های یک زاویه باقی می ماند ـــ مسلماً بیرون یک دایره. سه نوع از زوایا بیرون یک دایره قرار می گیرند، و تمامی آنها از تانژانت ها (tangents) و سکانت ها (secants) تشکیل شده اند.

شما می دانید تانژانت (مماس) چیست (فصل 14 را ببینید)، و در اینجا تعریف سِکانت (خط قاطع) را داریم: از نظر فنی، یک سکانت خطی است که یک دایره را در دو نقطه قطع می کند. اما سکانت هایی که در این بخش و در ادامۀ این فصل استفاده خواهید کرد، پاره خطهایی هستند که از میان یک دایره عبور می کنند و یک نقطۀ پایانی در بیرون آن دایره و یک نقطۀ پایانی در درون آن دایره دارند.

خوب، در اینجا سه نوع زاویه داریم که بیرون یک دایره قرار دارند:

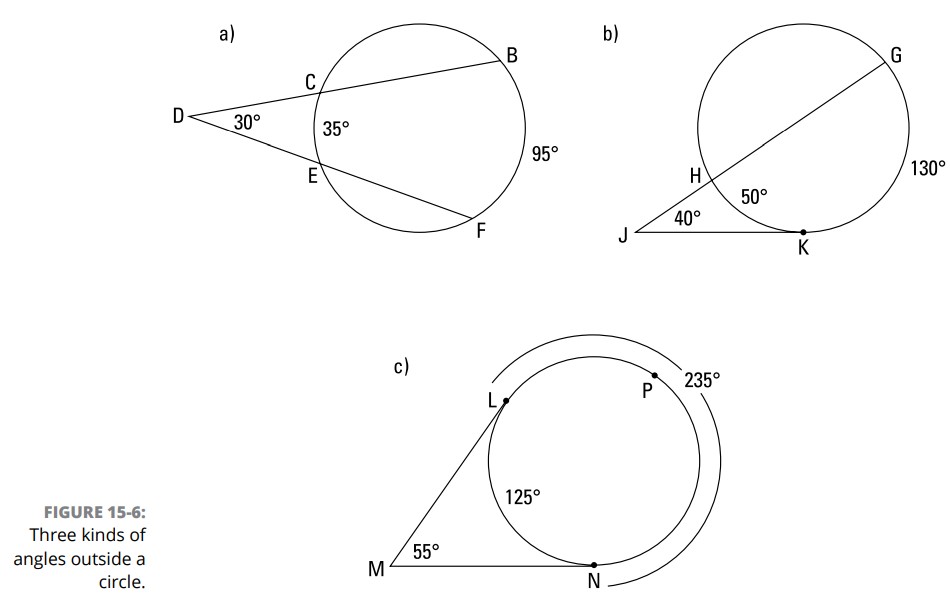
زاویۀ سکانت-سکانت (Secant-secant angle): یک زاویۀ سکانت-سکانت، مانند $\angle{BDF}$ در بخش a از شکل 6-15 ، زاویه ای است که رأس آن بیرون یک دایره قرار گرفته باشد و اضلاع آن دو سکانت از این دایره باشند.
زاویۀ سکانت-تانژانت (Secant-tangent angle): یک زاویۀ سکانت-تانژانت، مانند $\angle{GJK}$ در بخش b از شکل 6-15 ، زاویه ای است که رأس آن بیرون یک دایره قرار گرفته باشد و اضلاع آن یک سکانت و یک تانژانت از آن دایره باشند.
زاویۀ تانژانت-تانژانت (Tangent-tangent angle): یک زاویۀ تانژانت-تانژانت، مانند $\angle{LMN}$ در بخش c از شکل 6-15، زاویه ای می باشد که رأس آن بیرون دایره قرار گرفته باشد و اضلاع آن دو تانژانت از آن دایره باشند.

اندازۀ یک زاویه در بیرون دایره (Measure of an angle outside a circle): اندازۀ یک زاویۀ سکانت-سکانت، یک زاویۀ سکانت-تانژانت، یا یک زاویۀ تانژانت-تانژانت برابر با یک دوم تفاضل بین اندازه های کمان های جدا شده می باشد. به عنوان مثال، در شکل 6-15 :
$$
\angle{BDF} = \frac{1}{2} \bigl( m\overparen{BF}-m\overparen{CE} \bigr) \\
\angle{GJK} = \frac{1}{2} \bigl( m\overparen{GK}-m\overparen{HK} \bigr) \\
\angle{LMN} = \frac{1}{2} \bigl( m\overparen{LPN}-m\overparen{LN} \bigr)
$$

توجه داشته باشید که شما کمان کوچکتر را از کمان بزرگتر تفریق می کنید. (اگر به یک پاسخ منفی برسید، خواهید دانست که ترتیب تفریق را اشتباه انجام داده اید.)

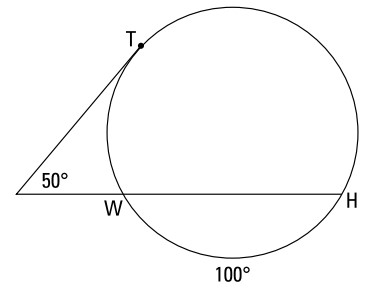
در اینجا مسأله ای داریم که فرمول زاویۀ بیرون یک دایره را نشان می دهد:

داده ها:
شکل هندسی به نحویکه می بینید
پیدا کنید:
$m\overparen{WT}$ و $m\overparen{TH}$

شما می دانید که حاصل جمع کمان های $\overparen{HW}$ ، $\overparen{WT}$، و $\overparen{TH}$ باید برابر با $360^{\circ}$ گردد، پس از آنجا که $\overparen{HW}$ برابر با $100^{\circ}$ است، $\overparen{WT}$ و $\overparen{TH}$ روی هم رفته $260^{\circ}$ می باشند. از این رو، شما می توانید $m\overparen{WT}$ را برابر با $x$ و $m\overparen{TH}$ را برابر با $260-x$ قرار دهید. این عبارتها را در فرمول جایگذاری کنید، و قسمت سخت کار را با موفقیت انجام داده اید:
$$
\text{Measure of } \angle{} \text{ outside circle} = \frac{1}{2}(\text{arc}-\text{arc}) \\
50 = \frac{1}{2}(m\overparen{TH}-m\overparen{WT}) \\
50 = \frac{1}{2}((260-x)-x) \\
50 = \frac{1}{2}(260-2x) \\
50=130-x \\
-80=-x \\
x=80
$$

ترجمۀ فرمول:
Measure of angle outside circle : اندازۀ زاویۀ بیرون دایره
arc: کمان

بنابراین $m\overparen{WT}$ برابر با $80^{\circ}$ ، و $m\overparen{TH}$ برابر با $180^{\circ}$ می باشد.

کدام فرمول زاویه-کمان را باید استفاده کنم؟

من دو نکتۀ عالی دارم که به شما کمک می کنند به یاد بیاورید، چه زمانی باید از کدام یک از این سه فرمول کمان-زاویه استفاده کنید.

در سه بخش پیشین، شما شش نوع از زوایا را مشاهده کردید که از وترها، سکانت ها، و تانژانت ها، ساخته شده بودند اما فقط سه فرمول زاویه-کمان را داشتید. همانطور که از روی عناوین هر کدام از این سه بخش می توانید بگویید، برای تعیین اینکه کدامیک از این سه فرمول زاویه-کمان را باید استفاده کنید، تنها چیزی که باید به آن دقت کنید، محل قرارگیریِ رأس آن زاویه می باشد: درون دایره، روی محیط دایره، یا بیرون دایره. شما نباید در مورد اینکه آیا دو ضلع این زاویه وتر، تانژانت، یا سکانت، یا ترکیبی از اینها می باشند، نگران باشید.

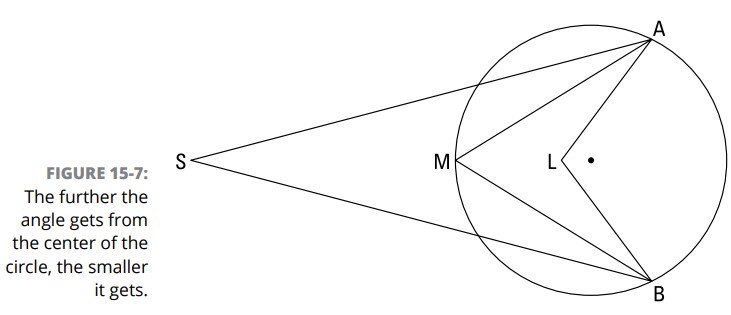
دومین نکته می تواند به شما کمک کند بیاد بیاورید که کدام فرمول با کدام دسته بندی از زاویه مرتبط است. ابتدا، شکل 7-15 را بررسی کنید.

شما می توانید ببینید که زاویۀ کوچکتر، $\angle{S}$ (شاید در حدود $35^{\circ}$) بیرون دایره قرار دارد؛ زاویۀ متوسط، $\angle{M}$ (در حدود $70^{\circ}$) روی محیط دایره قرار دارد؛ و زاویۀ بزرگتر، $\angle{L}$ (تقریباً $110^{\circ}$) درون دایره قرار دارد. در اینجا یک روش برای درک اینکه چرا اندازۀ این زوایا در این ترتیب پیش می روند داریم. فرض کنید اضلاع $\angle{L}$ قابل ارتجاع (مانند کش) می باشند. تجسم کنید $\angle{L}$ را در رأس آن با دست گرفته اید و آن را به سمت چپ می کشید (به نحویکه دو انتهای این کش به نقاط $A$ و $B$ متصل باقی بمانند). هر چقدر $\angle{L}$ را بیشتر به سمت چپ بکشید، این زاویه کوچکتر می شود.

تفریق چیزها را کوچکتر می کند، و جمع چیزها را بزرگتر می کند، اینطور نیست؟ خوب در اینجا چگونگی به یاد آوردن اینکه کدام فرمول زاویه-کمان را باید استفاده کنید، می بینید (شکل 7-15 را ببینید):

برای رسیدن به زاویۀ کوچکتر، تفریق می کنید:
$$\angle{S}=\frac{1}{2}(arc-arc)$$
برای رسیدن به زاویۀ متوسط، هیچ کاری انجام نمی دهید:
$$\angle{M}=\frac{1}{2}(arc)$$
برای رسیدن به زاویۀ بزرگتر، جمع می کنید:
$$\angle{L}=\frac{1}{2}(arc+arc)$$

(نکته: هرگاه که هر کدام از این فرمول های زاویه-کمان را استفاده می کنید، مطمئن شوید که شما همواره از کمان هایی استفاده می کنید که در درون زوایا قرار دارند.)

آموزش قبلی صفحۀ اصلی دوره آموزش بعدی