خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
معادلات خط و دایره
اگر دورۀ جبر 1 را گذرانده باشید، احتمالاً با نمودارهای خطها در دستگاه مختصات برخورد کرده باشید. نمودارهای دایره ها ممکن است چیز جدیدی برای شما باشد، اما بزودی خواهید دید که هیچ چیز خاصی ندارد. مسلماً خطها و دایره ها، بسیار متفاوتند. یکی راست و دیگر منحنی است. یکی بی نهایت و دیگری محدود است. اما چیز مشترک بین آنها این می باشد که هیچکدام از آنها یک آغاز یا پایان ندارند، و شما می توانید در امتداد هر کدام از آنها تا پایان زمان مسافرت کنید.

در مورد مستقیم و باریک صحبت کنید! خطها بی نهایت طولانی هستند، کاملاً سرراست هستند، و با این وجود تصور کردنش مشکل است، بی نهایت باریکتر از یک تار مو هستند.
در بخش 5، شما تمامی انواع ویژگیها، فرمولها، و قضایای جذاب در مورد دایره را دیدید، که هیچ ارتباطی با موقعیت و محل قرارگیری یک دایره ندارند. در این بخش، به لطف ادب و تواضع دکارت، شما در این مورد که دایره ها یک جایگاهی دارند تحقیق می کنید؛ شما موقعیت دایره ها را در دستگاه مختصات x-y با استفاده از روش های تحلیلی (analytic methods) ـــ یعنی با معادلات و جبر ـــ تحلیل می کنید. به عنوان مثال، یک ارتباط زیبای تحلیلی بین معادلۀ یک دایره و فرمول مسافت هر نقطه بر روی محیط آن دایره وجود دارد، زیرا هر نقطه بر روی یک دایره با مرکز آن دارای فاصلۀ یکسانی می باشد (برای جزئیات بیشتر در این زمینه مسأله ارائه شده به عنوان مثال را ببینید).
برای یک مسالۀ دایره آماده اید؟ بفرمایید:
داده ها:
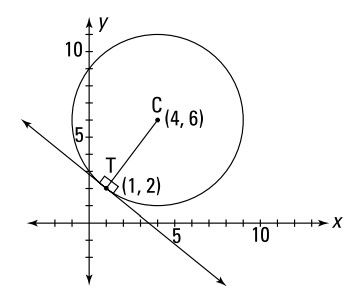
مرکز دایرۀ \(C\) در \((4,6)\) و تانژانت آن با یک خط در \((1,2)\) می باشد
پیدا کنید:

معادلات خط (Line equations)
در مورد مستقیم و باریک صحبت کنید! خطها بی نهایت طولانی هستند، کاملاً سرراست هستند، و با این وجود تصور کردنش مشکل است، بی نهایت باریکتر از یک تار مو هستند.
در اینجا شکل های پایه ای معادلات خط را داریم:
-
شکل شیب-تقاطع (Slope-intercept form): هنگامی که شیب یک خط (slope) و عرض از مبدأ (y-intercept) آن را می دانید (یا به سادگی می توانید آنها را بیابید)، از این شکل استفاده کنید.
$$y=mx+b$$
در این معادله، \(m\) شیب خط و \(b\) عرض از مبدأ آن می باشد.
-
شکل نقطه-شیب (Point-slope form): هنگامی که عرض از مبدأ یک خط را نمی دانید اما مختصات یک نقطه بر روی آن خط را می دانید، این ساده ترین شکل می باشد؛ شما همچنین نیاز به دانستن شیب این خط دارید.
$$y-y_1=m(x-x_1)$$
در این معادله \(m\) شیب خط و \((x_1,y_1)\) یک نقطه بر روی این خط می باشد.
-
خط افقی (Horizontal line): این شکل برای خطهایی که شیب آنها صفر می باشد استفاده می شود.
$$y=b$$
\(b\) (یا عددی که در \(b\) جایگذاری می شود) به شما می گوید که این خط در امتداد محور y چقدر بالا یا پایین است. توجه داشته باشید که هر نقطه ای در امتداد یک خط افقی دارای مختصات y یکسانی می باشد، که همان \(b\) می شود. در صورتیکه کنجکاو باشید، این شکل معادله یک مورد خاص از \(y=mx+b\) است که در آن \(m=0\) است.
-
خط عمودی (Vertical line): و در اینجا معادلۀ خطی را داریم که شیب آن تعریف نشده (undefined) می باشد.
$$x=a$$
در این معادله \(a\) طول از مبدأ (undefined) می باشد.
\(a\) (یا عددی که در \(a\) جایگذاری می شود) به شما می گوید که این خط در امتداد محور x چقدر رو به سمت راست یا چپ قرار دارد. هر نقطه ای در امتداد یک خط عمودی دارای مختصات \(x\) یکسانی که همان \(a\) است، می باشد.
معادلات مربوط به خطهای افقی و عمودی را با یکدیگر اشتباه نگیرید. این اشتباه به وفور رایج است. از آنجا که یک خط افقی با محور x موازی می باشد، شما ممکن است با خودتان فکر کنید که معادلۀ یک خط افقی \(x=a\) می باشد. و از آنجایی که یک خط عمودی با محور y موازی می باشد، همینطور ممکن است فکر کنید که معادلۀ یک خط عمودی \(y=b\) است. اما همانطور که در معادلات قبلی دیدید، ماجرا دقیقاً برعکس این است.
معادلۀ استاندارد دایره (standard circle equation)
در بخش 5، شما تمامی انواع ویژگیها، فرمولها، و قضایای جذاب در مورد دایره را دیدید، که هیچ ارتباطی با موقعیت و محل قرارگیری یک دایره ندارند. در این بخش، به لطف ادب و تواضع دکارت، شما در این مورد که دایره ها یک جایگاهی دارند تحقیق می کنید؛ شما موقعیت دایره ها را در دستگاه مختصات x-y با استفاده از روش های تحلیلی (analytic methods) ـــ یعنی با معادلات و جبر ـــ تحلیل می کنید. به عنوان مثال، یک ارتباط زیبای تحلیلی بین معادلۀ یک دایره و فرمول مسافت هر نقطه بر روی محیط آن دایره وجود دارد، زیرا هر نقطه بر روی یک دایره با مرکز آن دارای فاصلۀ یکسانی می باشد (برای جزئیات بیشتر در این زمینه مسأله ارائه شده به عنوان مثال را ببینید).
در اینجا معادلات دایره را داریم:
-
دایره ای که در مبدأ، \((0,0)\)، قرار گرفته است:
$$x^2+y^2=r^2$$
در این معادله \(r\) شعاع این دایره می باشد.
-
دایره ای که در هر نقطه ای، \((h,k)\)، قرار گرفته باشد:
$$(x-h)^2+(y-k)^2=r^2$$
در این معادله \((h,k)\) مرکز دایره و \(r\) شعاع آن می باشد.
(همانطور که ممکن است از دورۀ جبر به خاطر داشته باشید، تفریق هر عدد مثبت \(h\) از \(x\) در واقع دایره را به سمت راست حرکت می دهد؛ و تفریق هر عدد مثبت \(k\) از \(y\) دایره را به سمت بالا حرکت می دهد؛ افزودن یک عدد به \(x\) دایره را رو به سمت چپ، و افزودن یک عدد مثبت به \(y\) دایره را به سمت پایین حرکت می دهد.)
برای یک مسالۀ دایره آماده اید؟ بفرمایید:

داده ها:
مرکز دایرۀ \(C\) در \((4,6)\) و تانژانت آن با یک خط در \((1,2)\) می باشد
پیدا کنید:
-
معادلۀ این دایره
-
طول از مبدأ و عرض از مبدأ این دایره
-
معادلۀ خط مماس (تانژانت)
-
معادلۀ این دایره را بیابید.
تمام چیزی که برای معادلۀ یک دایره به آن نیاز دارید، مرکز و شعاع آن می باشد. در حال حاضر مرکز را دارید. شعاع یک دایره صرفاً فاصلۀ بین مرکز آن تا هر نقطه بر روی محیط دایره می باشد. از آنجا که نقطۀ تماس در مسأله داده شده است، از این نقطه استفاده می کنید.
$$
\text{Distance}_{C \text{ to } T}=\sqrt{(4-1)^2+(6-2)^2} \\
=\sqrt{3^2+4^2} \\
=5
$$
اکنون با جایگذاری مختصات مرکز و شعاع درون معادلۀ عمومی دایره، کار را تمام می کنید:
$$
(x-h)^2+(y-k)^2=r^2 \\
(x-4)^2+(y-6)^2=5^2
$$
-
طول از مبدأ و عرض از مبدأ این دایره را بیابید.
برای یافتن طول از مبدأها (x-intercepts) برای هر معادله ای، کافیست \(0\) را در \(y\) جایگذاری کنید و آن معادله را برای یافتن \(x\) حل کنید:
$$
(x-4)^2+(y-6)^2=5^2 \\
(x-4)^2+(0-6)^2=5^2 \\
(x-4)^2+36=25 \\
(x-4)^2=-11
$$
شما نمی توانید چیزی را مربع کنید و به یک عدد منفی برسید، بنابراین این معادله پاسخی ندارد؛ از اینرو، این دایره هیچ طول از مبدأیی ندارد. (من می دانم که شما می توانید صرفاً به تصویر نگاه کنید و از روی آن تشخیص دهید که این دایره با محور x تقاطعی ندارد، اما می خواستم به شما نشان بدهم که به لحاظ ریاضی چگونه می توانید این مسأله را تایید کنید.)
برای یافتن عرض از مبدأها (y-intercepts)، \(0\) را در \(x\) جایگذاری کنید و معادله را برای بدست آوردن \(y\) حل کنید:
$$
(0-4)^2+(y-6)^2=5^2 \\
16+(y-6)^2=25 \\
(y-6)^2=9 \\
y-6=\pm \sqrt{9} \\
y=\pm2+6 \\
y=3 \text{ or } 9
$$
بدین ترتیب عرض از مبدأهای این دایره \((0,3)\) و \((0,9)\) می باشند.
-
معادلۀ خط مماس (tangent line) را بیابید.
برای معادلۀ یک خط، شما نیاز به یک نقطه دارید (که هم اکنون آن را دارید) و همینطور به شیب خط نیاز دارید. در فصل 14 شما دریافتید که یک خط مماس بر شعاعی که به نقطۀ تماس ترسیم شده است، عمود می باشد. بنابراین، کافیست شیب آن شعاع را محاسبه کنید، و سپس قرینۀ معکوس (opposite reciprocal) آن، شیب خط مماس می باشد:
$$
\text{Slope}=\frac{y_2-y_1}{x_2-x_1} \\
\text{Slope}_{\text{Radius }\overline{CT}}=\frac{6-2}{4-1}=\frac{4}{3}
$$
بنابراین :
$$
\text{Slope}_{\text{Tangent line}}=-\frac{3}{4}
$$
اکنون این شیب و مختصات نقطۀ تماس را در شکل نقطه-شیب (point-slope form) از معادلۀ خط قرار می دهید:
$$
y-y_1=m(x-x_1) \\
y-2=-\frac{3}{4}(x-1)
$$
حالا آن را اندکی تر و تمیزتر می کنیم:
$$
4(y-2)=-3(x-1) \\
4y-8=-3x+3 \\
3x+4y=11
$$
مسلماً اگر به جای این شکل از معادلۀ خط، شما تصمیم می گرفتید که از شکل شیب-تقاطع (slope-intercept form) استفاده کنید، به نتیجۀ زیر می رسیدید:
$$
y=-\frac{3}{4}x+\frac{11}{4}
$$
تمام.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: