خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
بازتاب در هندسه (Reflection)

تبدیل (transformation) یک شکل در دستگاه مختصات x-y را می گیرد ـــ فرض کنید یک مثلث، متوازی الاضلاع، چندضلعی، هرچیزی ـــ و آن را به یک شکل مرتبط تبدیل می کند. به شکل گرفته شده توسط تبدیل، شکل سابق (before) و همینطور تصویر پیشین (pre-image) گفته می شود و به شکل تولید شده طی این فرآیند، شکل بعدی (after) و همینطور تصویر (image) گفته می شود. این تبدیل ممکن است تصویر اصلی را بزرگتر یا کوچکتر کند، آن را بپیچاند و به یک نسخۀ خنده دار از آن تبدیل کند (مانند وقتیکه در آینه های خمیده خودتان را نگاه می کنید)، شکل را بچرخاند، آن را به یک موقعیت جدید سُر بدهد، آن را چپه کند ـــ یا ممکن است تبدیل این شکل را در چندین ترکیب از این روش ها تغییر بدهید.

در این فصل، با یک زیرمجموعۀ خاص از تبدیلات که ایزومتری ها (isometries) نامیده می شوند، کار خواهید کرد. اینها تبدیلاتی هستند که در آنها شکلهای قبل و بعد از تبدیل با یکدیگر همنهشت (congruent) می باشند، که همانطور که می دانید، بدین معنا می باشد که این شکلها دقیقاً اشکال یکسان و هم اندازه ای هستند. من چهار نوع از ایزومتری ها را تشریح می کنم: بازتاب ها (reflections)، انتقال ها (translations)، دوران ها (rotations)، و لغزه ها (glide reflections). این بحث ها با بازتاب ها، که بلوک سازندۀ اصلی سه نوع دیگر ایزومتری ها می باشند، آغاز می گردد.
توجه: در این فصل از شما خواسته می شود که شیب ها، نقاط میانی، فاصله ها، عمود منصف ها، و معادلات خط را در دستگاه مختصات بیابید. اگر در مورد این چیزها نیاز به یک پیش زمینه دارید، به فصل 18 مراجعه کنید.
یک بازتاب هندسی (geometric reflection)، همانطور که به نظر می رسد، همانند یک بازتاب در آینه عمل می کند. شکل 1-19 شخصی را در برابر آینه نشان می دهد که به بازتاب یک مثلث که بر روی زمین مقابل آینه قرار دارد، نگاه می کند. توجه: تصویر \(\triangle{ABC}\) در آینه با حروف یکسانی نامگذاری شده است، با این استثناء که یک نماد پریم (prime symbol) به هر کدام از این حروف اضافه شده است \((\triangle{A'B'C'})\). بیشتر شکلهای هندسی تبدیل به این شیوه مورد رسیدگی قرار می گیرند.
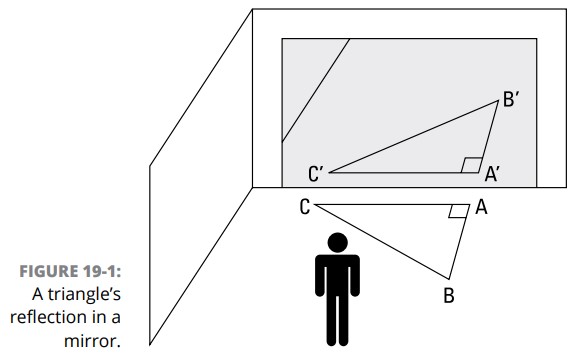
همانطور که می بینید، تصویر این مثلث در آینه در مقایسه با مثلث واقعی، پُشت و رو شده است. آینه ها (و به زبان ریاضی، بازتاب ها) همواره این نوع از وارونه کردن را تولید می کنند. وارونه کردن یک شکل، جهت (orientation) آن را تغییر می دهد، موضوعی که در بخش بعدی در موردش بحث خواهم کرد.
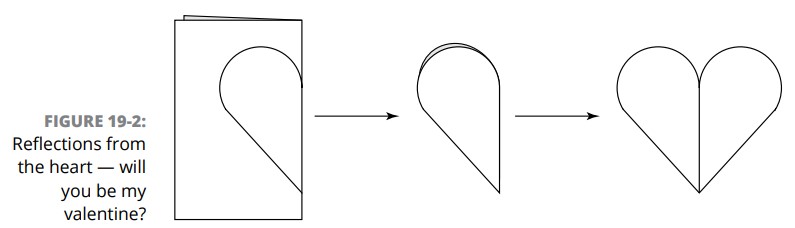
شکل 2-19 به شما نشان می دهد که یک بازتاب همچنین می تواند به شکل یک تاشُدن مورد تفکر قرار گیرد. در سمت چپ، شما یک برگۀ تاشده را می بینید که یک شکل قلب نصفه بر روی آن ترسیم شده است؛ در وسط، شما آن قلب نصف شده را می بینید که بریده شده است؛ و در سمت راست، آن قلب را به صورت باز شده می بینید. سمت چپ و راست این قلب به طرز آشکاری شکل یکسانی دارند. هر سمت، بازتاب سمت دیگر می باشد. این چین یا خط تا که از مرکز قلب رو به پایین می رود، خط بازتاب (reflecting line) نامیده می شود، که در ادامۀ این فصل در موردش بحث خواهم کرد.
من در ادامۀ این فصل انتقال ها، دوران ها، و لغزه ها را مورد بحث قرار خواهم داد. اما قبل از اینکه به سراغ آنها بروید، به طور خلاصه جهت (orientation) را مورد بحث قرار می دهم و سپس چگونگی حل کردن مسأله های بازتاب را به شما نشان می دهم.
در شکل 3-19 ، \(\triangle{PQR}\) از این سو به آن سوی خط \(l\) بازتاب یافته است تا \(\triangle{P'Q'R'}\) تولید گردد. مثلث های \(\triangle{PQR}\) و \(\triangle{P'Q'R'}\) همنهشت می باشند، اما جهت آنها متفاوت است:
توجه کنید که ـــ مانند قلب نشان داده شده در شکل 2-19 ـــ بازتاب نمایش داده شده در شکل 3-19 می تواند به عنوان یک تاشُدن مورد تفکر قرار گیرد. اگر شما این صفحه را از این سو به آن سوی خط \(l\) تا کنید، \(\triangle{PQR}\) کاملاً بر روی \(\triangle{P'Q'R'}\) قرار خواهد گرفت، \(P\) بر روی \(P'\)، \(Q\) بر روی \(Q'\)، و \(R\) بر روی \(R'\) .
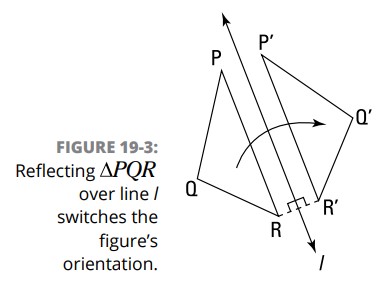
در یک بازتاب، خط بازتاب دهنده، خطی است که بر روی آن تصویر پیشین (pre-image) بازتاب می یابد. شکل 3-19 یک ویژگی مهم از خطهای بازتاب دهنده را نشان می دهد: اگر با متصل کردن نقطۀ \(R\) در تصویر پیشین به نقطۀ \(R'\) در تصویر، \(\overline{RR'}\) را بسازید (یا \(P\) با \(P'\) یا \(Q\) با \(Q'\))، خط بازتاب، یعنی \(l\)، عمود منصف (perpendicular bisector) \(\overline{RR'}\) خواهد بود.
در اینجا مسأله ای داریم که از این مفهوم استفاده می کند: در شکل زیر، \(\triangle{J'K'L'}\) بازتاب \(\triangle{JKL}\) بر روی یک خط بازتاب دهنده، می باشد. با استفاده از نقاط \(J\) و \(J'\) ، معادلۀ این خط بازتاب دهنده را بیابید. سپس تصدیق کنید که این خط بازتاب دهنده \(K\) را به \(K'\) و \(L\) را به \(L'\) ارسال می کند.

خط بازتاب دهنده، عمود منصف پاره خطهایی می باشد که نقاط تصویر پیشین را به نقاط تصویر متصل می کنند. از آنجا که عمود منصف یک پاره خط از نقطۀ میانی آن پاره خط می گذرد، اولین چیزی که برای یافتن معادلۀ خط بازتاب دهنده نیاز به انجام دادنش دارید اینست که نقطۀ میانی \(\overline{JJ'}\) را بیابید:
$$
\text{Midpoint}=\biggl( \frac{x_1+x_2}{2},\frac{y_1+y_2}{2} \biggr) \\
\text{Midpoint}_{\overline{JJ'}}=\biggl( \frac{-1+11}{2},\frac{9+3}{2} \biggr) \\
=(5,6)
$$
سپس، به شیب \(\overline{JJ'}\) نیاز دارید:
$$
\text{Slope}=\frac{y_2-y_1}{x_2-x_1} \\
\text{Slope}_{\overline{JJ'}}=\frac{3-9}{11-(-1)}=\frac{-6}{12}=-\frac{1}{2}
$$
شیب عمود منصف \(\overline{JJ'}\) قرینۀ معکوس شیب \(\overline{JJ'}\) می باشد (همانطور که در فصل 18 توضیح دادم). \(\overline{JJ'}\) دارای شیب \(-\frac{1}{2}\) می باشد، پس شیب عمود منصف، و بنابراین شیب خط بازتاب دهنده، برابر با \(2\) می باشد. اکنون می توانید با جایگذاری این شیب \(2\) و نقطۀ \((5,6)\) در شکل نقطه-شیب از معادلۀ این خط، بخش اول این مسأله را به پایان برسانید:
$$
y-y_1=m(x-x_1) \\
y-6=2(x-5) \\
y=2x-10+6 \\
y=2x-4
$$
این معادلۀ خط بازتاب دهنده در شکل شیب-تقاطع می باشد.
برای تصدیق اینکه، این خط بازتاب دهنده، \(K\) را به \(K'\) و \(L\) را به \(L'\) ارسال می کند، شما باید نشان دهید که این خط، عمود منصفِ \(\overline{KK'}\) و \(\overline{LL'}\) می باشد. برای انجام این کار، باید نشان دهید که نقاط میانی \(\overline{KK'}\) و \(\overline{LL'}\) بر روی این خط قرار گرفته اند و شیب \(\overline{KK'}\) و \(\overline{LL'}\) هر دو برابر با \(-\frac{1}{2}\) است (قرینۀ معکوس شیب خط بازتاب دهنده، یعنی خط \(y=2x-4\)). ابتدا، در اینجا نقطۀ میانی \(\overline{KK'}\) را داریم:
$$
\text{Midpoint}_{\overline{KK'}}=\biggl( \frac{2+14}{2},\frac{15+9}{2} \biggr) \\
=(8,12)
$$
این مختصات ها را در معادلۀ \(y=2x-4\) جایگذاری کنید تا ببینید آیا درست کار می کنند. از آنجا که \(12=2(8)-4\) ، نقطۀ میانی \(\overline{KK'}\) بر روی خط بازتاب دهنده قرار دارد. اکنون شیب \(\overline{KK'}\) را بدست آورید:
$$\text{Slope}_{\overline{KK'}}=\frac{9-15}{14-2}=\frac{-6}{12}=-{1\over2}$$
این شیب مطلوب می باشد، بنابراین همه چیز برای \(K\) و \(K'\) عالی است. اکنون نقطۀ میانی \(\overline{LL'}\) را بدست آورید:
$$
\text{Midpoint}_{\overline{LL'}}=\biggl( \frac{5+9}{2},\frac{11+9}{2} \biggr) \\
=(7,10)
$$
بررسی کنید وقتیکه این مختصات را در معادلۀ خط بازتاب دهنده، یعنی \(y=2x-4\) ، جایگذاری می کنید، بدرستی کار کند. از آنجا که \(10=2(7)-4\) ، نقطۀ میانی \(\overline{LL'}\) بر روی این خط قرار دارد. در پایان، شیب \(\overline{LL'}\) را بیابید:
$$\text{Slope}_{\overline{LL'}}=\frac{9-11}{9-5}=\frac{-2}{4}=-{1\over2}$$
درست است. شما با موفقیت این مسأله را به پایان رساندید.

در این فصل، با یک زیرمجموعۀ خاص از تبدیلات که ایزومتری ها (isometries) نامیده می شوند، کار خواهید کرد. اینها تبدیلاتی هستند که در آنها شکلهای قبل و بعد از تبدیل با یکدیگر همنهشت (congruent) می باشند، که همانطور که می دانید، بدین معنا می باشد که این شکلها دقیقاً اشکال یکسان و هم اندازه ای هستند. من چهار نوع از ایزومتری ها را تشریح می کنم: بازتاب ها (reflections)، انتقال ها (translations)، دوران ها (rotations)، و لغزه ها (glide reflections). این بحث ها با بازتاب ها، که بلوک سازندۀ اصلی سه نوع دیگر ایزومتری ها می باشند، آغاز می گردد.
توجه: در این فصل از شما خواسته می شود که شیب ها، نقاط میانی، فاصله ها، عمود منصف ها، و معادلات خط را در دستگاه مختصات بیابید. اگر در مورد این چیزها نیاز به یک پیش زمینه دارید، به فصل 18 مراجعه کنید.
بازتاب ها (Reflections)
یک بازتاب هندسی (geometric reflection)، همانطور که به نظر می رسد، همانند یک بازتاب در آینه عمل می کند. شکل 1-19 شخصی را در برابر آینه نشان می دهد که به بازتاب یک مثلث که بر روی زمین مقابل آینه قرار دارد، نگاه می کند. توجه: تصویر \(\triangle{ABC}\) در آینه با حروف یکسانی نامگذاری شده است، با این استثناء که یک نماد پریم (prime symbol) به هر کدام از این حروف اضافه شده است \((\triangle{A'B'C'})\). بیشتر شکلهای هندسی تبدیل به این شیوه مورد رسیدگی قرار می گیرند.

همانطور که می بینید، تصویر این مثلث در آینه در مقایسه با مثلث واقعی، پُشت و رو شده است. آینه ها (و به زبان ریاضی، بازتاب ها) همواره این نوع از وارونه کردن را تولید می کنند. وارونه کردن یک شکل، جهت (orientation) آن را تغییر می دهد، موضوعی که در بخش بعدی در موردش بحث خواهم کرد.
شکل 2-19 به شما نشان می دهد که یک بازتاب همچنین می تواند به شکل یک تاشُدن مورد تفکر قرار گیرد. در سمت چپ، شما یک برگۀ تاشده را می بینید که یک شکل قلب نصفه بر روی آن ترسیم شده است؛ در وسط، شما آن قلب نصف شده را می بینید که بریده شده است؛ و در سمت راست، آن قلب را به صورت باز شده می بینید. سمت چپ و راست این قلب به طرز آشکاری شکل یکسانی دارند. هر سمت، بازتاب سمت دیگر می باشد. این چین یا خط تا که از مرکز قلب رو به پایین می رود، خط بازتاب (reflecting line) نامیده می شود، که در ادامۀ این فصل در موردش بحث خواهم کرد.

بازتاب ها بلوک سارندۀ سه ایزومتری دیگر می باشند: شما می توانید سه ایزومتری دیگر را با یکسری از بازتاب ها تولید کنید:
-
انتقال ها (Translations) معادل دو بازتاب می باشند.
-
دوران ها (Rotations) معادل دو بازتاب می باشند.
-
لغزه ها (Glide reflections) معادل سه بازتاب می باشند.
من در ادامۀ این فصل انتقال ها، دوران ها، و لغزه ها را مورد بحث قرار خواهم داد. اما قبل از اینکه به سراغ آنها بروید، به طور خلاصه جهت (orientation) را مورد بحث قرار می دهم و سپس چگونگی حل کردن مسأله های بازتاب را به شما نشان می دهم.
جهت (orientation)
در شکل 3-19 ، \(\triangle{PQR}\) از این سو به آن سوی خط \(l\) بازتاب یافته است تا \(\triangle{P'Q'R'}\) تولید گردد. مثلث های \(\triangle{PQR}\) و \(\triangle{P'Q'R'}\) همنهشت می باشند، اما جهت آنها متفاوت است:
-
یک روش برای اینکه ببینید اینها دارای جهت های متفاوتی می باشند اینست که شما نمی توانید \(\triangle{PQR}\) و \(\triangle{P'Q'R'}\) را بدون چپه کردن آنها بر روی همدیگر قرار دهید ـــ مهم نیست که چگونه آنها را می چرخانید یا به اطراف می لغزانید.
-
ویژگی دوم اشکال دارای جهت متفاوت اینست که به صورت ساعتگرد/خلاف جهت ساعتگرد منتقل شده اند. توجه کنید که در \(\triangle{PQR}\) ، شما به صورت خلاف عقربه های ساعت از \(P\) به \(Q\) به \(R\) می روید، اما در مثلث بازتافته، یعنی \(\triangle{P'Q'R'}\) ، شما به صورت ساعتگرد از \(P'\) به \(Q'\) به \(R'\) می روید.
توجه کنید که ـــ مانند قلب نشان داده شده در شکل 2-19 ـــ بازتاب نمایش داده شده در شکل 3-19 می تواند به عنوان یک تاشُدن مورد تفکر قرار گیرد. اگر شما این صفحه را از این سو به آن سوی خط \(l\) تا کنید، \(\triangle{PQR}\) کاملاً بر روی \(\triangle{P'Q'R'}\) قرار خواهد گرفت، \(P\) بر روی \(P'\)، \(Q\) بر روی \(Q'\)، و \(R\) بر روی \(R'\) .

بازتاب ها و جهت (Reflections and orientation): یک مرتبه بازتاب دادن یک شکل جهت آن را تغییر می دهد. اگر یک شکل را بیش از یکبار بازتاب دهید، قوانین زیر اعمال می شوند:
-
اگر یک شکل را بازتاب دهید و سپس دوباره آن را روی خط یکسانی یا خط متفاوتی بازتاب دهید، آن شکل به جهت اصلی خودش باز می گردد. به طور عمومی تر، اگر شکلی را به تعداد دفعات زوجی بازتاب دهید، نتیجۀ نهایی شکلی خواهد بود که جهت آن با جهت شکل اصلی یکسان می باشد.
-
بازتاب دادن یک شکل به تعداد دفعاتی فرد، شکلی را تولید می کند که جهت آن مخالف جهت شکل اصلی می باشد.
یافتن یک خط بازتاب دهنده (reflecting line)
در یک بازتاب، خط بازتاب دهنده، خطی است که بر روی آن تصویر پیشین (pre-image) بازتاب می یابد. شکل 3-19 یک ویژگی مهم از خطهای بازتاب دهنده را نشان می دهد: اگر با متصل کردن نقطۀ \(R\) در تصویر پیشین به نقطۀ \(R'\) در تصویر، \(\overline{RR'}\) را بسازید (یا \(P\) با \(P'\) یا \(Q\) با \(Q'\))، خط بازتاب، یعنی \(l\)، عمود منصف (perpendicular bisector) \(\overline{RR'}\) خواهد بود.
یک خط بازتاب دهنده یک عمود منصف می باشد: هنگامی که یک شکل بازتافته می شود، خط بازتاب دهنده، عمود منصف تمامی پاره خطهایی است که نقاط تصویر پیشین را به نقاط متناظر آنها در تصویر، متصل می کنند.
در اینجا مسأله ای داریم که از این مفهوم استفاده می کند: در شکل زیر، \(\triangle{J'K'L'}\) بازتاب \(\triangle{JKL}\) بر روی یک خط بازتاب دهنده، می باشد. با استفاده از نقاط \(J\) و \(J'\) ، معادلۀ این خط بازتاب دهنده را بیابید. سپس تصدیق کنید که این خط بازتاب دهنده \(K\) را به \(K'\) و \(L\) را به \(L'\) ارسال می کند.

خط بازتاب دهنده، عمود منصف پاره خطهایی می باشد که نقاط تصویر پیشین را به نقاط تصویر متصل می کنند. از آنجا که عمود منصف یک پاره خط از نقطۀ میانی آن پاره خط می گذرد، اولین چیزی که برای یافتن معادلۀ خط بازتاب دهنده نیاز به انجام دادنش دارید اینست که نقطۀ میانی \(\overline{JJ'}\) را بیابید:
$$
\text{Midpoint}=\biggl( \frac{x_1+x_2}{2},\frac{y_1+y_2}{2} \biggr) \\
\text{Midpoint}_{\overline{JJ'}}=\biggl( \frac{-1+11}{2},\frac{9+3}{2} \biggr) \\
=(5,6)
$$
سپس، به شیب \(\overline{JJ'}\) نیاز دارید:
$$
\text{Slope}=\frac{y_2-y_1}{x_2-x_1} \\
\text{Slope}_{\overline{JJ'}}=\frac{3-9}{11-(-1)}=\frac{-6}{12}=-\frac{1}{2}
$$
شیب عمود منصف \(\overline{JJ'}\) قرینۀ معکوس شیب \(\overline{JJ'}\) می باشد (همانطور که در فصل 18 توضیح دادم). \(\overline{JJ'}\) دارای شیب \(-\frac{1}{2}\) می باشد، پس شیب عمود منصف، و بنابراین شیب خط بازتاب دهنده، برابر با \(2\) می باشد. اکنون می توانید با جایگذاری این شیب \(2\) و نقطۀ \((5,6)\) در شکل نقطه-شیب از معادلۀ این خط، بخش اول این مسأله را به پایان برسانید:
$$
y-y_1=m(x-x_1) \\
y-6=2(x-5) \\
y=2x-10+6 \\
y=2x-4
$$
این معادلۀ خط بازتاب دهنده در شکل شیب-تقاطع می باشد.
برای تصدیق اینکه، این خط بازتاب دهنده، \(K\) را به \(K'\) و \(L\) را به \(L'\) ارسال می کند، شما باید نشان دهید که این خط، عمود منصفِ \(\overline{KK'}\) و \(\overline{LL'}\) می باشد. برای انجام این کار، باید نشان دهید که نقاط میانی \(\overline{KK'}\) و \(\overline{LL'}\) بر روی این خط قرار گرفته اند و شیب \(\overline{KK'}\) و \(\overline{LL'}\) هر دو برابر با \(-\frac{1}{2}\) است (قرینۀ معکوس شیب خط بازتاب دهنده، یعنی خط \(y=2x-4\)). ابتدا، در اینجا نقطۀ میانی \(\overline{KK'}\) را داریم:
$$
\text{Midpoint}_{\overline{KK'}}=\biggl( \frac{2+14}{2},\frac{15+9}{2} \biggr) \\
=(8,12)
$$
این مختصات ها را در معادلۀ \(y=2x-4\) جایگذاری کنید تا ببینید آیا درست کار می کنند. از آنجا که \(12=2(8)-4\) ، نقطۀ میانی \(\overline{KK'}\) بر روی خط بازتاب دهنده قرار دارد. اکنون شیب \(\overline{KK'}\) را بدست آورید:
$$\text{Slope}_{\overline{KK'}}=\frac{9-15}{14-2}=\frac{-6}{12}=-{1\over2}$$
این شیب مطلوب می باشد، بنابراین همه چیز برای \(K\) و \(K'\) عالی است. اکنون نقطۀ میانی \(\overline{LL'}\) را بدست آورید:
$$
\text{Midpoint}_{\overline{LL'}}=\biggl( \frac{5+9}{2},\frac{11+9}{2} \biggr) \\
=(7,10)
$$
بررسی کنید وقتیکه این مختصات را در معادلۀ خط بازتاب دهنده، یعنی \(y=2x-4\) ، جایگذاری می کنید، بدرستی کار کند. از آنجا که \(10=2(7)-4\) ، نقطۀ میانی \(\overline{LL'}\) بر روی این خط قرار دارد. در پایان، شیب \(\overline{LL'}\) را بیابید:
$$\text{Slope}_{\overline{LL'}}=\frac{9-11}{9-5}=\frac{-2}{4}=-{1\over2}$$
درست است. شما با موفقیت این مسأله را به پایان رساندید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: