خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
انتقال در هندسه (translation)
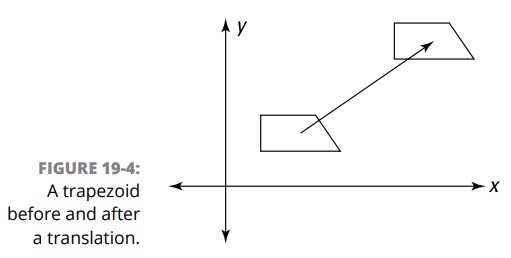
انتقال (translation) ـــ احتمالاً ساده ترین نوع تبدیل ـــ یک تبدیل است که در آن یک شکل بدون هیچ کج شدن یا چرخش، صرفاً به یک موقعیت جدید سُر می خورد. مشاهدۀ اینکه یک انتقال جهت یک شکل را تغییر نمی دهد، مشکل نیست. شکل 4-19 را ببینید.

ممکن است اندکی شگفت آور باشد، اما به جای سُر دادن یک شکل به یک موقعیت جدید، شما می توانید با بازتافتن آن شکل بر روی یک خط و سپس بر روی خط دوم، به نتیجۀ نهایی یکسانی برسید.
شما با انجام کار زیر می توانید چگونگی کارکرد این مطلب را ببینید: یک برگه کاغذ سفید بردارد و یک تکه از گوشۀ پایین و سمت راست آن را پاره کنید. آن برگه کاغذ را در مقابل خودتان و بر روی یک میز قرار دهید. حالا آن کاغذ را بر روی لبۀ راست آن به سمت راست برگردانید ـــ به نحویکه لبۀ سمت راست آن حرکت نکند. سپس پشت آن کاغذ را خواهید دید، و گوشۀ پاره شده در سمت چپ و پایین قرار خواهد داشت. در پایان، دوباره آن کاغذ را به سمت راست برگردانید. اکنون، بعد از دو بار برگرداندن، یا دو بازتاب، آن کاغذ را در همان شکل اصلی اش خواهید دید، با این تفاوت که هم اکنون به سمت راست سُر خورده است، یا منتقل شده است.
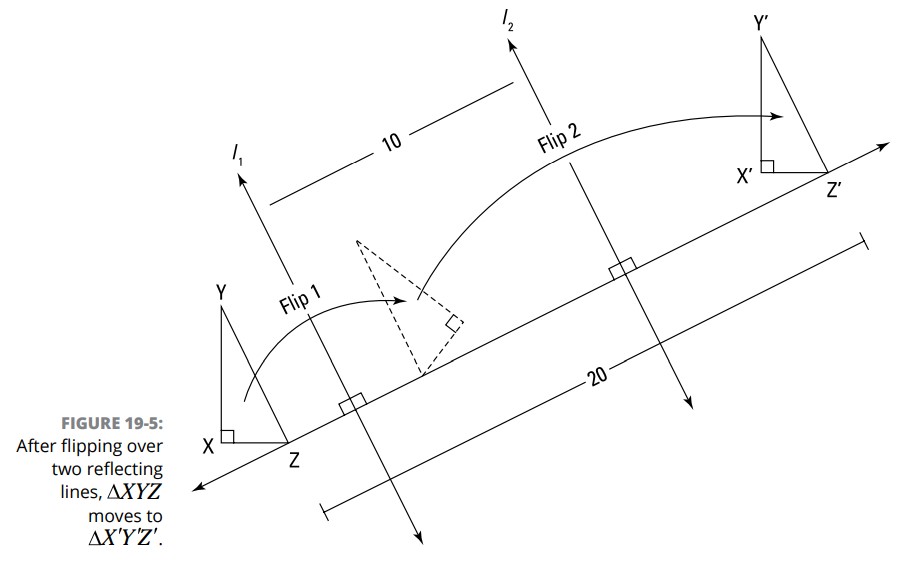
آیا این قضیه دهان پر کن است؟ به جای اینکه در این تئوری درگیر تفکر عمیق شوید، نگاهی به شکل 5-19 بیندازید تا ببینید چگونه خطهای بازتاب دهنده در یک انتقال کار می کنند.
در اینجا چندین نکته در مورد شکل 5-19 داریم. شما می توانید ببینید که مسافت انتقال (فاصلۀ بین \(Z\) تا \(Z'\)) برابر با \(20\) می باشد؛ که فاصلۀ بین خطهای بازتاب دهنده، یعنی \(l_1\) و \(l_2\) ، نصف آن می باشد؛ و آن خطهای بازتاب دهندۀ \(l_1\) و \(l_2\) بر خط انتقال \(\overleftrightarrow{ZZ'}\) عمود می باشند.
من انتخاب کرده ام تا این دو خط بازتاب دهنده را بین تصویر پیشین و تصویر قرار دهم، زیرا این ساده ترین روش برای مشاهدۀ چگونگی کارکرد آنها می باشد. اما خطهای بازتاب دهنده مجبور نیستند که در آنجا قرار بگیرند.
بهترین روش برای فهمیدن قضیه انتقال (translation theorem) بررسی یک مسألۀ مثال می باشد. مسألۀ بعدی چگونگی یافتن یک خط انتقال، مسافت انتقال، و یک جفت از خطهای بازتاب دهنده را به شما نشان می دهد.
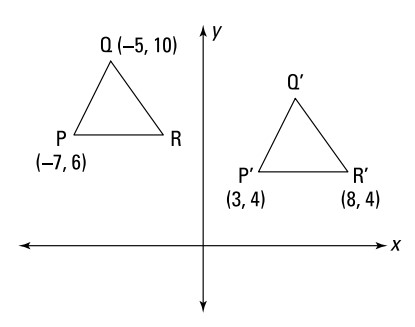
در شکل زیر، تصویر پیشین مثلث \(\triangle{PQR}\) به سمت پایین و راست تا تصویر مثلث \(\triangle{P'Q'R'}\) سُر خورده است.
داده ها:
مختصات های \(P\)، \(P'\)، \(Q\)، و \(R'\) به نحویکه می بینید
پیدا کنید:


یک انتقال برابر با دو بازتاب است
ممکن است اندکی شگفت آور باشد، اما به جای سُر دادن یک شکل به یک موقعیت جدید، شما می توانید با بازتافتن آن شکل بر روی یک خط و سپس بر روی خط دوم، به نتیجۀ نهایی یکسانی برسید.
شما با انجام کار زیر می توانید چگونگی کارکرد این مطلب را ببینید: یک برگه کاغذ سفید بردارد و یک تکه از گوشۀ پایین و سمت راست آن را پاره کنید. آن برگه کاغذ را در مقابل خودتان و بر روی یک میز قرار دهید. حالا آن کاغذ را بر روی لبۀ راست آن به سمت راست برگردانید ـــ به نحویکه لبۀ سمت راست آن حرکت نکند. سپس پشت آن کاغذ را خواهید دید، و گوشۀ پاره شده در سمت چپ و پایین قرار خواهد داشت. در پایان، دوباره آن کاغذ را به سمت راست برگردانید. اکنون، بعد از دو بار برگرداندن، یا دو بازتاب، آن کاغذ را در همان شکل اصلی اش خواهید دید، با این تفاوت که هم اکنون به سمت راست سُر خورده است، یا منتقل شده است.
خط انتقال و فاصلۀ انتقال : در یک انتقال، خط انتقال (translation line) هر خطی است که یک نقطه بر روی تصویر پیشین (pre-image) از یک شکل را به نقطۀ متناظر آن در تصویر (image) متصل می کند؛ خط انتقال جهت انتقال را به شما نشان می دهد. فاصلۀ انتقال (translation distance) مسافتی است که بین نقطۀ موجود بر روی تصویر پیشین و نقطۀ متناظر آن بر روی تصویر برقرار است.
یک انتقال برابر با دو بازتاب می باشد: یک انتقال از یک مسافت معین در امتداد یک خط انتقال برابر با دو بازتاب بر روی خطهایی موازی می باشد که:
-
بر خط انتقال عمود باشند
-
توسط یک مسافت که برابر با نصف مسافت انتقال می باشد، جدا شده باشند
توجه: این دو خط بازتاب دهندۀ موازی، یعنی \(l_1\) و \(l_2\) ، می توانند هر جایی در امتداد این خط انتقال باشند، مشروط بر اینکه:
-
آنها با نصف فاصلۀ انتقال جدا شده باشند
-
جهت از \(l_1\) به \(l_2\) با جهت از پیش تصویر به تصویر یکسان باشد
-
آنها با نصف فاصلۀ انتقال جدا شده باشند
آیا این قضیه دهان پر کن است؟ به جای اینکه در این تئوری درگیر تفکر عمیق شوید، نگاهی به شکل 5-19 بیندازید تا ببینید چگونه خطهای بازتاب دهنده در یک انتقال کار می کنند.
در اینجا چندین نکته در مورد شکل 5-19 داریم. شما می توانید ببینید که مسافت انتقال (فاصلۀ بین \(Z\) تا \(Z'\)) برابر با \(20\) می باشد؛ که فاصلۀ بین خطهای بازتاب دهنده، یعنی \(l_1\) و \(l_2\) ، نصف آن می باشد؛ و آن خطهای بازتاب دهندۀ \(l_1\) و \(l_2\) بر خط انتقال \(\overleftrightarrow{ZZ'}\) عمود می باشند.
من انتخاب کرده ام تا این دو خط بازتاب دهنده را بین تصویر پیشین و تصویر قرار دهم، زیرا این ساده ترین روش برای مشاهدۀ چگونگی کارکرد آنها می باشد. اما خطهای بازتاب دهنده مجبور نیستند که در آنجا قرار بگیرند.

یافتن عناصر یک انتقال
بهترین روش برای فهمیدن قضیه انتقال (translation theorem) بررسی یک مسألۀ مثال می باشد. مسألۀ بعدی چگونگی یافتن یک خط انتقال، مسافت انتقال، و یک جفت از خطهای بازتاب دهنده را به شما نشان می دهد.
در شکل زیر، تصویر پیشین مثلث \(\triangle{PQR}\) به سمت پایین و راست تا تصویر مثلث \(\triangle{P'Q'R'}\) سُر خورده است.

داده ها:
مختصات های \(P\)، \(P'\)، \(Q\)، و \(R'\) به نحویکه می بینید
پیدا کنید:
-
مختصات های \(Q'\) و \(R\)
-
مسافت انتقال
-
معادلۀ یک خط انتقال
-
معادلۀ دو جفت متفاوت از خطهای بازتاب دهنده
-
مختصات های \(Q'\) و \(R\) را بیابید.
از \(P(-7,6)\) به \(P'(3,4)\) ، شما \(10\) واحد به سمت راست و \(2\) واحد به سمت پایین حرکت می کنید. در یک انتقال، هر نقطه در تصویر پیشین به روش یکسانی به تصویر منتقل می گردد، بنابراین برای یافتن \(Q'\) ، کافیست از \(Q\) که در مختصات \((-5,10)\) می باشد، آغاز کنید و \(10\) واحد به سمت راست و \(2\) واحد پایین بروید. این کار شما را به \(Q'\) در \((5,8)\) می رساند.
برای بدست آوردن مختصات \(R\)، شما از \(R'\) آغاز می کنید و عقب گرد می کنید (یعنی \(10\) واحد رو به سمت چپ و \(2\) واحد رو به سمت بالا می روید). این کار \((-2,6)\) را به عنوان مختصات \(R\) به شما می دهد.
-
مسافت انتقال را بیابید.
مسافت انتقال (translation distance)، فاصلۀ بین هر نقطه در تصویر پیشین با نقطۀ متناظر آن در تصویر می باشد، مانند فاصلۀ بین \(P\) و \(P'\) . از فرمول مسافت استفاده کنید:
$$
\text{Distance}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\
\text{Distance}_{P \text{ to } P'}=\sqrt{(3-(-7))^2+(4-6)^2} \\
=\sqrt{10^2+(-2)^2} \\
=\sqrt{104}=2\sqrt{26} \approx 10.2 \text{ units}
$$
این پاسخ به شما می گوید که هر نقطه بر روی تصویر پیشین یک مسافت \(10.2\) واحدی را طی می کند تا به نقطۀ متناظر آن در تصویر برسد.
-
معادلۀ یک خط انتقال را بیابید.
شما می توانید از هر دو نقطه ای که \(\triangle{PQR}\) را به \(\triangle{P'Q'R'}\) متصل می کند به عنوان یک خط انتقال استفاده کنید. خطی که نقاط \(P\) و \(P'\) را به یکدیگر متصل می کند، همانند هر کدام دیگر از سایر این خطها کار می کند، بنابراین معادلۀ \(\overleftrightarrow{PP'}\) را به عنوان معادلۀ یک خط انتقال بدست آورید.
برای استفاده از شکل نقطه-شیب (point-slope form) برای معادلۀ \(\overleftrightarrow{PP'}\) ، شما به یک نقطه و شیب خط نیاز دارید. هم اکنون دو نقطه بر روی این خط دارید، نقاط \(P\) و \(P'\)، بنابراین هر کدام را که خواستید انتخاب کنید. فرمول شیب خط، چیز دیگری را که می خواهید به شما می دهد:
$$\text{Slope}_{\overleftrightarrow{PP'}}=\frac{4-6}{3-(-7)}=\frac{-2}{10}=-\frac{1}{5}$$
حالا این شیب و مختصات \(P'\) را در شکل نقطه-شیب جایگذاری کنید (\(P\) نیز بخوبی کار می کند، اما من تمایل دارم تا از اعداد منفی اجتناب کنم):
$$
y-y_1=m(x-x_1) \\
y-4=-{1\over5}(x-3)
$$
اگر دوست داشته باشید می توانید با اندکی جبر ساده این معادله را به شکل شیب-تقاطع (slope-intercept form) ببرید:
$$y=-\frac{1}{5}x+\frac{23}{5}$$
این معادلۀ یک خط انتقال می باشد. مثلث \(PQR\) می تواند در امتداد این خط تا \(\triangle{P'Q'R'}\) سُر بخورد.
-
معادلۀ دو جفت متفاوت از خطهای بازتاب دهنده را بیابید.
قضیۀ انتقال به شما می گوید که دو خط بازتاب دهنده که یک انتقال را به انجام می رسانند باید بر خط انتقال عمود باشند و با نصف مسافت انتقال از یکدیگر جدا شده باشند. بی نهایت از اینگونه جفت خط ها را می توان یافت. در اینجا یک روش ساده برای رسیدن به یک جفت از آنها را می بینید.
خطهای متعامد دارای شیب هایی می باشند که قرینۀ معکوس یکدیگرند. در بخش 3 از این مسأله، شما دریافتید که \(\overleftrightarrow{PP'}\) دارای شیب \(-\frac{1}{5}\) می باشد؛ ازینرو، از آنجایی که خطهای بازتاب دهنده بر \(\overleftrightarrow{PP'}\) عمود هستند، شیب آنها باید قرینۀ معکوس \(-\frac{1}{5}\) باشد، که برابر با \(5\) می باشد.
به عنوان اولین خط بازتاب دهنده، شما می توانید از خطی استفاده کنید که شیب آن \(5\) باشد و از میان \(P\) در مختصات \((-7,6)\) عبور کند. از شکل نقطه-شیب در معادلۀ خط استفاده کنید و آن را ساده سازی کنید:
$$
y-6=5(x-(-7)) \\
y=5x+41
$$
سپس از آنجا که مسافت انتقال برابر با طول \(\overline{PP'}\) می باشد، فاصلۀ بین \(P\) تا نقطۀ میانی \(\overline{PP'}\) نصف مسافت انتقال می باشد ـــ مسافت مطلوب بین خطهای بازتاب دهنده. بنابراین خط بازتاب دهندۀ دومتان را از نقطۀ میانی \(\overline{PP'}\) عبور دهید. ابتدا نقطۀ میانی را بیابید:
$$\text{Midpoint}_{\overline{PP'}}=\biggl( \frac{-7+3}{2}, \frac{6+4}{2} \biggr)=(-2,5)$$
دومین خط بازتاب دهنده، که با اولی موازی می باشد، همچنین دارای شیب \(5\) است. اعداد خود را در شکل شیب-تقاطع جایگذاری کنید و ساده سازی نمایید:
$$
y-5=5(x-(-2)) \\
y-5=5x+10 \\
y=5x+15
$$
بنابراین شما دو خط بازتاب دهنده تان را بدست آورده اید. اگر \(\triangle{PQR}\) را بر روی خط \(y=5x+41\) بازتاب دهید و سپس آن را بر روی خط \(y=5x+15\) بازتاب دهید (این بازتاب ها باید به همین ترتیب باشند)، \(\triangle{PQR}\) بر روی \(\triangle{P'Q'R'}\) فرود خواهد آمد، و هر نقطه دقیقاً روی نقطۀ دیگر قرار خواهد گرفت.
بعد از اینکه یک جفت از خطهای بازتاب دهنده را دانستید، بدون هیچ زحمتی می توانید به هر تعداد از این جفت ها که بخواهید را بیابید. تمامی خطهای بازتاب دهنده شیب یکسانی خواهند داشت، و در هر جفت از این خطها، عرض از مبدأهای آنها به یک اندازه از یکدیگر فاصله دارند.در این مسأله، تمامی خطهای بازتاب دهنده دارای شیب \(5\) می باشند، و هر جفت باید عرض از مبدأهایی داشته باشند که \(26\) واحد از یکدیگر فاصله داشته باشند ـــ مانند \(y=5x+41\) و \(y=5x+15\) . به عنوان مثال، جفت خطهای بازتاب دهندۀ زیر نیز می توانند این انتقال را به انجام برسانند:
$$
y=5x+27 \text{ and } y=5x+1 \text{ or } \\
y=5x+1,000,026 \text{ and } y=5x+1,000,000
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: