خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مکان هندسی (locus)

مکان هندسی (locus) یک واژۀ فانتزی برای کلمۀ مجموعه (set) می باشد. در یک مسالۀ مکان هندسی، کار شما اینست که یک شیء هندسی را که برخی شرایط را برآورده می کند، کشف کنید و سپس ترسیمش نمایید. در اینجا یک مثال ساده داریم: مکان هندسی یا مجموعۀ تمام نقاطی که از یک نقطۀ داده شده \(5\) واحد فاصله دارند، چه می باشد؟ پاسخ یک دایره می باشد زیرا اگر شما با یک نقطۀ داده شده آغاز کنید و سپس از آن نقطه \(5\) واحد در هر جهت فاصله بگیرید، به یک دایره با شعاع \(5\) می رسید.

ترسیم ها ممکن است بیشتر برای شما آشنا باشند. در یک مسالۀ ترسیم (Construction) کار شما اینست که از یک پرگار و خط کش استفاده کنید تا یک شکل موجود مانند یک زاویه یا یک مثلث را کپی کنید، یا چیزی شبیه عمود منصف یک پاره خط، نیمساز یک زاویه، یا ارتفاع های یک مثلث را رسم کنید.
چیزی که بین این دو موضوع مشترک می باشد اینست که هر دوی آنها شامل ترسیم مجموعه ای از نقاط که شکل هندسی خاصی را می سازند، می باشد. در مسأله های مکان هندسی، چالش ترسیم شکل نمی باشد؛ چالش اینست که کشف کنید مسأله چه شکلی را از شما می خواهد. در مسأله های ترسیم، برعکس آن است: شما دقیقاً می دانید چه شکلی را می خواهید، و چالش اینست که بفهمید چگونه باید آن را رسم کنید.
فرآیند حل کردن یک مسالۀ مکان هندسی، در صورتی که با متد معینی با آن روبرو نشوید، می تواند مشکل باشد. بنابراین در این بخش، یک روش چهار مرحله ای برای یافتن مکان هندسی ارائه می دهم که می تواند شما را از برخی اشتباهات رایج (مانند شامل کردن تعداد نقاط خیلی زیاد یا تعداد نقاط خیلی کم در پاسختان) برحذر دارد. سپس، چند مسالۀ دو بعدیِ مکان هندسی را به شما می دهم که از این فرآیند در آنها استفاده شده است، و سپس به شما نشان می دهم که چگونه از این مسأله های دو بعدی مکان هندسی برای حل کردن مسأله های مرتبط سه بعدی استفاده کنید.
در ادامه رویۀ راحت و سودمند حل کردن مسأله های مکان هندسی را که به شما قولش را داده بودم، می بینید. در مورد اینکه فوراً آن را درک کنید، نگران نباشید. به محض اینکه چند مسأله را که در ادامه آمده است حل کنید، برای شما واضح می گردد. (هشدار:با وجود اینکه شما اغلب در هنگام کار کردن با مراحل 2 و 3 به نتیجه ای نمی رسید، در بررسی آنها اهمال نورزید!):
در مسأله های مکان هندسی دو بعدی، تمامی نقاط در پاسخ مکان هندسی در یک صفحه قرار می گیرند. این معمولاً، و نه همیشه، همان صفحه ای می باشد که شیء هندسی داده شده، در آن قرار دارد. در چند مسأله به چگونگی کارکرد راه حل چهار مرحله ای در مسأله های دو بعدی نگاهی بیندازید.
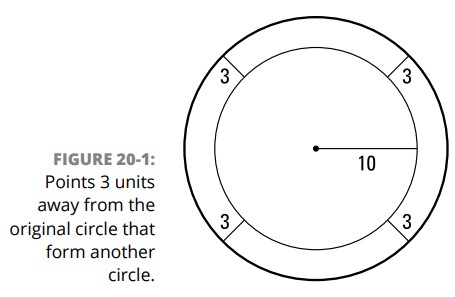
مکان هندسی تمامی نقاطی که از یک دایرۀ داده شده که شعاع آن \(10\) واحد است، \(3\) واحد فاصله دارند، چه می باشد؟
مکان هندسی تمامی نقاطی که از دو نقطۀ داده شده متساوی الفاصله می باشند، چیست؟
حالا فرض کنید مسالۀ دو به جای آن اینگونه می بود: مکان هندسی رأس های مثلث های متساوی الساقین که دارای یک پاره خط برای یک قاعده باشند، چیست؟
دوباره به شکل 4-20 نگاهی بیندازید. برای این مسالۀ اصلاح شده، \(\overline{AB}\) قاعدۀ مثلث های متساوی الساقین می باشد. از آنجا که رأسی از یک مثلث متساوی الساقین که ساق های همنهشت را به یکدیگر متصل می کند از نقاط پایانی قاعدۀ آن متساوی الفاصله می باشد (نقاط \(A\) و \(B\))، پاسخ این مسالۀ اصلاح شده با پاسخ مسالۀ دو یکسان می باشد ـــ با این تفاوت که، چه زمانی وارد مراحل 2 و 3 می شوید.
در مرحلۀ 1 از مسالۀ اصلاح شده، شما الگوی عمود منصف یکسانی را می یابید، بنابراین افتادن در این دام که فکر کنید این عمود منصف پاسخ نهایی می باشد، آسان است. اما وقتیکه وارد مرحلۀ دو می شوید، درخواهید یافت که شما باید نقاط داده شدۀ \(A\) و \(B\) را به پاسختان اضافه کنید، زیرا، مسلماً، آنها رأس هایی از همۀ مثلث ها می باشند.
و هنگامی که وارد مرحلۀ 3 می شوید، باید متوجه شوید که شما باید یک نقطۀ واحد را از مکان هندسی استثناء کنید: نقطۀ میانی \(\overline{AB}\) نمی تواند بخشی از پاسخ باشد زیرا بر روی همان خطی قرار دارد که نقاط \(A\) و \(B\) در آن قرار دارند، و شما نمی توانید از سه نقطۀ هم راستا به عنوان سه رأس یک مثلث استفاده کنید. از اینرو، مکان هندسی این مسالۀ اصلاح شده، عمود منصف \(\overline{AB}\) ، بعلاوۀ نقاط \(A\) و \(B\)، منهای نقطۀ میانی \(\overline{AB}\) می باشد.
حالا چگونه این نکته بر روی مسأله پیشین اعمال شده است: نقطه ای که شما در مرحلۀ 3 باید استثناء می کردید در نقطۀ میانی یک پاره خط قرار داشت.
با این حال نقاطی که باید اضافه می کردید (نقاط داده شده) نیز در این نکته لیست شده اند، این وضعیت غیرمعمول است. بیشتر اوقات، نقاطی که باید در مرحلۀ 2 اضافه گردند نوعی از نقاط خاص، یا جداشده در این لیست نمی باشند. در عوض، آنها معمولاً الگوی خودشان را فراتر از الگوی اول که شما تشخیص داده اید، تشکیل می دهند (شما این را در مسالۀ اول دیدید که در آن دایرۀ داخلی را فراموش کرده بودم).
نقاط \(P\) و \(R\) به شما داده شده اند، مکان هندسی نقاط \(Q\) به نحویکه \(\angle{PQR}\) یک زاویۀ قائمه را بسازد، چه می باشد؟
در مسأله های سه بعدی مکان هندسی، شما باید مکان هندسی تمامی نقاط را در یک فضای سه بعدی تعیین کنید که شرایط داده شده در مکان هندسی را برآورده می سازند. در این بخش کوتاه، به جای اینکه یک مسالۀ سه بعدی را از آغاز و بدون هیچ داده ای انجام بدهیم، من صرفاً می خواهم در مورد چگونگی مقایسۀ مسأله های سه بعدی مکان هندسی با مسأله های دو بعدی، بحث کنم.
برای اینکه درک واضحی از این نکتۀ سه بعدی داشته باشید، نگاهی به نسخۀ سه بعدی مسأله های سه بعدی مکان هندسی که در بخشهای پیشین مطرح شدند، بیندازید (من برای اینکه آنها را طبق ترتیب اصلیشان ذکر نکرده ام دلایلی دارم).
به شکل 4-20 ، که پاسخ مسالۀ دو را به شما نشان می دهد، باز گردید. همان مسأله را در نظر بگیرید، اما آن را یک مسالۀ سه بعدی کنید: مکان هندسی نقاطی در یک فضای سه بعدی که از دو نقطۀ داده شده متساوی الفاصله می باشند، چیست؟
پاسخ (به جای یک خط) یک صفحه می باشد که آن صفحه عمود منصف پاره خطی که این دو نقطه را به یکدیگر متصل کرده است، می باشد. در مورد این پاسخ به چند چیز توجه کنید:
اکنون نسخۀ اصلاح شدۀ مسالۀ دو را در نظر بگیرید. پاسخ آن را ممکن است بیاد بیاورید، که با پاسخ مسالۀ دو یکسان می باشد (یک عمود منصف)، اما با دو نقطۀ اضافه شده و یک نقطۀ حذف شده. این پاسخ دو بعدی در بصری سازی پاسخ سه بعدی به شما کمک می کند. پاسخ نسخۀ سه بعدی برابر با پاسخ نسخۀ دو بعدی که پیرامون \(\overleftrightarrow{AB}\) چرخانده شده است، می باشد، یعنی صفحۀ عمود منصف، بعلاوۀ نقاط \(A\) و \(B\) ، منهای نقطۀ میانی \(\overline{AB}\) .
نسخۀ سه بعدی مسالۀ سه (با نقطه های داده شدۀ \(P\) و \(R\)، مکان هندسی نقاط \(Q\) در فضا به نحویکه \(\angle{PQR}\) یک زاویۀ قائمه باشد، چیست؟) مسالۀ دیگری است که می توانید پاسخ سه بعدی را با چرخاندن پاسخ دو بعدی بدست آورید. شکل 6-20 که پیشتر نشان داده شد، این پاسخ دو بعدی را نشان داده و همینطور توصیف می کند: آن یک دایره منهای نقاط پایانی قطر \(\overline{PR}\) می باشد. اگر این پاسخ دو بعدی را پیرامون \(\overleftrightarrow{PR}\) بچرخانید، پاسخ سه بعدی را بدست می آورید: پاسخ یک کره با قطر \(\overline{PR}\)، منهای نقاط \(P\) و \(R\) می باشد.
شکل 2-20 که پیشتر نشان داده شد، پاسخ مسالۀ یک را نشان داده و توصیف می کند: دو دایرۀ متحدالمرکز. اما برخلاف سایر مسأله های سه بعدی در این بخش، پاسخ نسخۀ سه بعدی این مسأله (مکان هندسی تمامی نقاطی در فضا که سه واحد از دایرۀ داده شده با شعاع 10 واحد، فاصله دارند، چه می باشد؟) نمی تواند با چرخاندن پاسخ دو بعدی بدست آید. اگرچه، این پاسخ دو بعدی هنوز هم می تواند در تجسم کردن پاسخ سه بعدی به شما کمک کند، زیرا این پاسخ دو بعدی یک برش از پاسخ سه بعدی می باشد. آیا می توانید پاسخ سه بعدی را تجسم کنید؟ این پاسخ سه بعدی شکل یک دونات (donut) را دارد ـــ به زبان ریاضی به این شکل چنبره (torus) گفته می شود ـــ که عرض آن \(26\) واحد و عرض سوراخ آن \(14\) واحد می باشد. تجسم کنید که این دونات را به یک دستگاه برش نان شیرینی حلقوی (bagel slicer) برش زده اید. سطح مسطح هر کدام از این نصفه دونات ها یک دایرۀ کوچک در محل سوراخ دونات و یک دایرۀ بزرگ پیرامون لبۀ بیرونی دارد. به دو دایرۀ پررنگ در شکل 2-20 برگردید. آنها دو دایره ای را که در نصف دونات می بینید به شما نشان می دهند.

ترسیم ها ممکن است بیشتر برای شما آشنا باشند. در یک مسالۀ ترسیم (Construction) کار شما اینست که از یک پرگار و خط کش استفاده کنید تا یک شکل موجود مانند یک زاویه یا یک مثلث را کپی کنید، یا چیزی شبیه عمود منصف یک پاره خط، نیمساز یک زاویه، یا ارتفاع های یک مثلث را رسم کنید.
چیزی که بین این دو موضوع مشترک می باشد اینست که هر دوی آنها شامل ترسیم مجموعه ای از نقاط که شکل هندسی خاصی را می سازند، می باشد. در مسأله های مکان هندسی، چالش ترسیم شکل نمی باشد؛ چالش اینست که کشف کنید مسأله چه شکلی را از شما می خواهد. در مسأله های ترسیم، برعکس آن است: شما دقیقاً می دانید چه شکلی را می خواهید، و چالش اینست که بفهمید چگونه باید آن را رسم کنید.
مسأله های مکان های هندسی
مکان هندسی (Locus): یک مکان هندسی مجموعه ای از نقاط است (معمولاً نوعی از اشیاء هندسی مانند یک خط یا یک دایره) شامل همۀ نقاط و فقط نقاطی که برخی شرایط خاص را برآورده می سازند.
یادداشت مترجم: کلمۀ loci به معنای مکان های هندسی، جمع کلمۀ Locus (مکان هندسی) می باشد.
فرآیند حل کردن یک مسالۀ مکان هندسی، در صورتی که با متد معینی با آن روبرو نشوید، می تواند مشکل باشد. بنابراین در این بخش، یک روش چهار مرحله ای برای یافتن مکان هندسی ارائه می دهم که می تواند شما را از برخی اشتباهات رایج (مانند شامل کردن تعداد نقاط خیلی زیاد یا تعداد نقاط خیلی کم در پاسختان) برحذر دارد. سپس، چند مسالۀ دو بعدیِ مکان هندسی را به شما می دهم که از این فرآیند در آنها استفاده شده است، و سپس به شما نشان می دهم که چگونه از این مسأله های دو بعدی مکان هندسی برای حل کردن مسأله های مرتبط سه بعدی استفاده کنید.
روش چهار مرحله ای برای مسأله های مکان هندسی
در ادامه رویۀ راحت و سودمند حل کردن مسأله های مکان هندسی را که به شما قولش را داده بودم، می بینید. در مورد اینکه فوراً آن را درک کنید، نگران نباشید. به محض اینکه چند مسأله را که در ادامه آمده است حل کنید، برای شما واضح می گردد. (هشدار:با وجود اینکه شما اغلب در هنگام کار کردن با مراحل 2 و 3 به نتیجه ای نمی رسید، در بررسی آنها اهمال نورزید!):
-
یک الگو را شناسایی کنید.
گاهی اوقات کلید این الگو بلافاصله برای شما آشکار می شود. اگر اینطور باشد در همین مرحلۀ 1 شما کارتان را تمام کرده اید. اگر اینطور نباشد، یک نقطۀ واحد را بیابید که شرط یا شرایط داده شده در مسالۀ مکان هندسی را برآورده سازد؛ آن گاه نقطۀ مشابه دومی را بیابید؛ سپس، سومی؛ و به همین ترتیب، تا زمانی که یک الگو را شناسایی کنید.
-
به دنبال نقاطی خارج از الگو برای افزودن باشید.
در خارج از الگویی که در مرحلۀ 1 شناسایی کرده اید به دنبال نقاطی اضافی باشید که شرط یا شرایط داده شده را برآورده سازند.
-
در داخل الگو به دنبال نقاطی برای استثناء کردن باشید.
در درون الگویی که در مرحلۀ 1 شناسایی کرده اید (و احتمالاً، هر چند احتمال خیلی کمی دارد، هر الگویی که ممکن است در مرحلۀ 2 یافته باشید) به دنبال نقاطی باشید که علیرغم این حقیقت که متعلق به این الگو هستند، در برآورده ساختن شرط یا شرایط داده شده شکست بخورند.
- یک شکل هندسی ترسیم کنید و شرحی را بر پاسخ مکان هندسی بنویسید.
مسأله های دو بعدی مکان هندسی
در مسأله های مکان هندسی دو بعدی، تمامی نقاط در پاسخ مکان هندسی در یک صفحه قرار می گیرند. این معمولاً، و نه همیشه، همان صفحه ای می باشد که شیء هندسی داده شده، در آن قرار دارد. در چند مسأله به چگونگی کارکرد راه حل چهار مرحله ای در مسأله های دو بعدی نگاهی بیندازید.
مسالۀ یک
مکان هندسی تمامی نقاطی که از یک دایرۀ داده شده که شعاع آن \(10\) واحد است، \(3\) واحد فاصله دارند، چه می باشد؟
-
الگویی را شناسایی کنید.
در یک مسأله این احتمال وجود دارد که بدون اینکه وارد رویۀ یک نقطه در هر بار شوید، بتوانید الگویی را تجسم کنید. هنگامی که شما می خوانید که تمامی نقاطی را می خواهید که \(3\) واحد از یک دایره فاصله دارند، می توانید ببینید که یک دایرۀ بزرگتر، شما را به نتایج مطلوب می رساند. شکل 1-20 دایرۀ داده شده با شعاع \(10\) و دایره ای با شعاع \(13\) را نشان می دهد که شما به عنوان پاسخ آن را ترسیم کرده اید.
-
به دنبال نقاطی خارج از الگو برای افزودن باشید.
آیا می بینید مرحلۀ 1 به چه چیزی اشاره نکرده است؟ درست است ـــ آن یک دایرۀ کوچکتر با شعاع \(7\) می باشد که درون دایره اصلی قرار دارد (شکل 2-20 را ببینید). من گمان می کنم فراموش کردن این دایرۀ دوم توسط من اندکی ساختگی بوده است، و فرض می گیرم که بسیاری از افراد فوراً در می یابند که این پاسخ باید شامل هر دو دایره باشد. اگرچه، افراد معمولاً بر روی الگوی خاصی تمرکز می کنند (در این مسأله دایرۀ بزرگتر) ، به نحویکه هر چیز دیگر را حذف می کنند. ذهن آنها به نوعی گرفتار یک عادت شده است، و آنها در دیدن هر چیز دیگری به غیر از الگو یا ایدۀ اول که در آن گیر کرده اند، مشکل دارند. و به همین دلیل هم می باشد که وارد این مرحلۀ دوم از این روش چهار مرحله ای شدن، بسیار مهم است.
-
در داخل الگو به دنبال نقاطی برای استثناء کردن باشید.
تمامی نقاط از شعاع \(7\) واحدی و شعاع \(13\) واحدی در دایره ها، شرایط داده شده را برآورده می سازند، بنابراین هیچ نقطه ای نیاز به استثناء شدن ندارد.
-
مکان هندسی را ترسیم کنید و شرحی بر آن بنویسید.
شکل 2-20 این مکان هندسی را به شما نشان می دهد، و عنوانش آن را توصیف می کند.
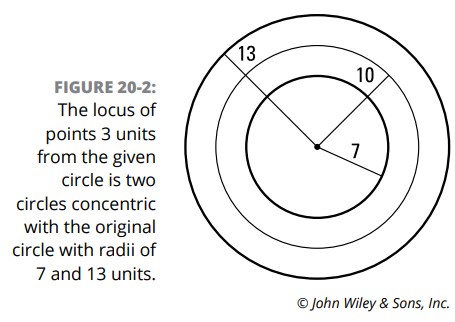
ترجمۀ شکل: مکان هندسی نقاطی که از دایرۀ داده شده \(3\) واحد فاصله دارند، دو دایرۀ متحدالمرکز با دایرۀ اصلی می باشند که شعاع های آنها \(7\) و \(13\) واحد هستند.
مسالۀ دو
مکان هندسی تمامی نقاطی که از دو نقطۀ داده شده متساوی الفاصله می باشند، چیست؟
-
الگویی را مشخص سازید.
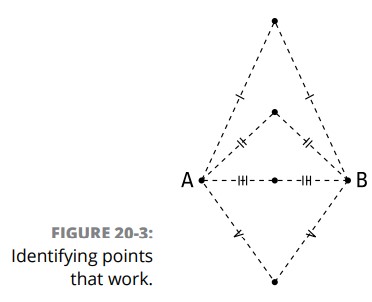
شکل 3-20 این دو نقطۀ داده شده را به شما نشان می دهد، \(A\) و \(B\)، همراه با چهار نقطۀ جدید که هر کدامشان از این نقاط داده شده فاصلۀ یکسانی دارند.
آیا این الگو را می بینید؟ درست فهمیدید ـــ آن یک خط عمودی است که از وسط نقطۀ میانی پاره خطی که این دو نقطۀ داده شده را به یکدیگر متصل می کند، عبور می کند. به عبارت دیگر، عمود منصف آن پاره خط می باشد.
-
خارج از الگو را بررسی کنید.
این بار در مرحلۀ دو به نتیجه ای نمی رسید. هر نقطۀ دیگری را که در عمود منصف \(\overline{AB}\) قرار ندارد، بررسی کنید، و خواهید دید که از نقاط \(A\) و \(B\) متساوی الفاصله نخواهد بود. از اینرو، هیچ نقطه ای برای افزودن ندارید.
-
داخل الگو را بررسی کنید.
هیچ چیز قابل توجهی در اینجا نیز وجود ندارد. هر نقطه ای بر روی عمود منصف \(\overline{AB}\) ، در واقع از نقاط \(A\) و \(B\) هم فاصله می باشد. (شما ممکن است این را از قضیۀ دوم متساوی الفاصله که در فصل 9 مطرح شد، به یاد داشته باشید.) از اینرو، هیچ نقطه ای برای استثناء کردن وجود ندارد. (تکرار هشدار: به خودتان اجازه ندهید اندکی تنبل شوید و مراحل 2 و 3 را نادیده بگیرید!)
-
مکان هندسی را ترسیم کنید و آن را با واژگان توصیف کنید.
شکل 4-20 این مکان هندسی را نشان می دهد، و عنوان آن توصیفش می کند.
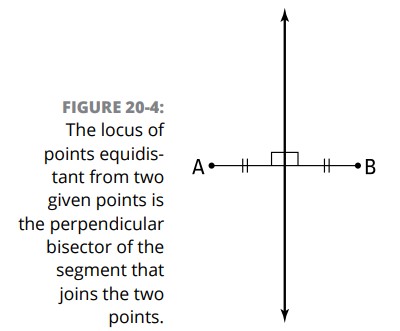
ترجمۀ شکل: مکان هندسی نقاطی که از دو نقطۀ داده شده متساوی الفاصله می باشند، عمود منصف پاره خطی است که این دو نقطه را به هم متصل کرده است.
حالا فرض کنید مسالۀ دو به جای آن اینگونه می بود: مکان هندسی رأس های مثلث های متساوی الساقین که دارای یک پاره خط برای یک قاعده باشند، چیست؟
دوباره به شکل 4-20 نگاهی بیندازید. برای این مسالۀ اصلاح شده، \(\overline{AB}\) قاعدۀ مثلث های متساوی الساقین می باشد. از آنجا که رأسی از یک مثلث متساوی الساقین که ساق های همنهشت را به یکدیگر متصل می کند از نقاط پایانی قاعدۀ آن متساوی الفاصله می باشد (نقاط \(A\) و \(B\))، پاسخ این مسالۀ اصلاح شده با پاسخ مسالۀ دو یکسان می باشد ـــ با این تفاوت که، چه زمانی وارد مراحل 2 و 3 می شوید.
در مرحلۀ 1 از مسالۀ اصلاح شده، شما الگوی عمود منصف یکسانی را می یابید، بنابراین افتادن در این دام که فکر کنید این عمود منصف پاسخ نهایی می باشد، آسان است. اما وقتیکه وارد مرحلۀ دو می شوید، درخواهید یافت که شما باید نقاط داده شدۀ \(A\) و \(B\) را به پاسختان اضافه کنید، زیرا، مسلماً، آنها رأس هایی از همۀ مثلث ها می باشند.
و هنگامی که وارد مرحلۀ 3 می شوید، باید متوجه شوید که شما باید یک نقطۀ واحد را از مکان هندسی استثناء کنید: نقطۀ میانی \(\overline{AB}\) نمی تواند بخشی از پاسخ باشد زیرا بر روی همان خطی قرار دارد که نقاط \(A\) و \(B\) در آن قرار دارند، و شما نمی توانید از سه نقطۀ هم راستا به عنوان سه رأس یک مثلث استفاده کنید. از اینرو، مکان هندسی این مسالۀ اصلاح شده، عمود منصف \(\overline{AB}\) ، بعلاوۀ نقاط \(A\) و \(B\)، منهای نقطۀ میانی \(\overline{AB}\) می باشد.
اگر یک نقطه نیاز به استثناء شده داشته باشد، باید چیزی خاص یا غیرمعمول در مورد آن وجود داشته باشد. هنگامی که به دنبال نقاطی از یک مکان هندسی برای استثناء کردن می باشید، نقاطی را که در محل هایی خاص قرار دارند بررسی کنند، مانند:
-
نقاط داده شده
-
نقاط میانی و نقاط پایانی در پاره خطها
-
نقاط تماس بر روی محیط یک دایره
حالا چگونه این نکته بر روی مسأله پیشین اعمال شده است: نقطه ای که شما در مرحلۀ 3 باید استثناء می کردید در نقطۀ میانی یک پاره خط قرار داشت.
با این حال نقاطی که باید اضافه می کردید (نقاط داده شده) نیز در این نکته لیست شده اند، این وضعیت غیرمعمول است. بیشتر اوقات، نقاطی که باید در مرحلۀ 2 اضافه گردند نوعی از نقاط خاص، یا جداشده در این لیست نمی باشند. در عوض، آنها معمولاً الگوی خودشان را فراتر از الگوی اول که شما تشخیص داده اید، تشکیل می دهند (شما این را در مسالۀ اول دیدید که در آن دایرۀ داخلی را فراموش کرده بودم).
مسالۀ سه
نقاط \(P\) و \(R\) به شما داده شده اند، مکان هندسی نقاط \(Q\) به نحویکه \(\angle{PQR}\) یک زاویۀ قائمه را بسازد، چه می باشد؟
-
الگویی را مشخص سازید.
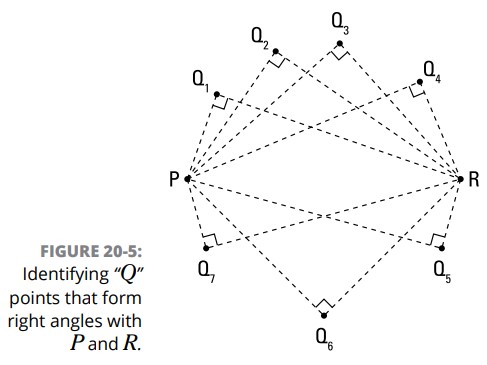
پیدا کردن این الگو ممکن است اندکی مهارت آمیز باشد، اما اگر با نقاط \(P\) و \(R\) آغاز کنید و سعی کنید تا چندین نقطۀ \(Q\) را بیابید که با \(P\) و \(R\) زاویۀ قائمه می سازند، احتمالاً شروع به دیدن الگویی کنید که ظهور می کند. شکل 5-20 را ببینید.
آیا الگو را دیدید؟ نقاط \(Q\) شروع به شکل دادن یک دایره با قطر \(\overline{PR}\) می کنند (شکل 6-20 را ببینید). اگر در مورد قضیۀ زاویۀ محاطی (inscribed-angle theorem) که در فصل 15 گفته شد، فکر کنید، این موضوع معنا دار می گردد: در یک دایره با \(\overline{PR}\) به عنوان قطر آن، کمان نیم دایره \(\overparen{PR}\) برابر با \(180^{\circ}\) خواهد بود، بنابراین تمامی زوایای محاطی \(PQR\) برابر با نصف آن یعنی \(90^{\circ}\) خواهند بود.
-
خارج از الگو را بررسی کنید.
نه، هیچ چیزی برای افزودن در اینجا نیست. هر نقطۀ \(Q\) درون این دایره که در مرحلۀ 1 تعیین کردید یک زاویۀ منفرجه (obtuse angle) و یا یک زاویۀ نیم صفحه (straight angle) را با \(P\) و \(R\) می سازد، و هر نقطه ای بیرون این دایره یک زاویۀ حاده (acute angle) یا یک زاویۀ صفر درجه را با \(P\) و \(R\) می سازد. تمامی زوایای قائمه بر روی محیط دایره قرار دارند. (محل قرارگیری این سه نوع زاویه ـــ حاده، قائمه، منفرجه ـــ از قضیۀ زاویه-دایره در فصل 15 تبعیت می کند.)
-
درون الگو را بررسی کنید.
خودشه! ببینید کدام نقاط را باید استثناء کنید؟ این نقاط، نقاط داده شدۀ \(P\) و \(R\) می باشند. اگر \(Q\) در محل قرارگیری هر کدام از این دو نقطۀ داده شده، قرار گیرد، چیزی که برای شما باقی می ماند یک پاره خط می باشد (\(\overline{QR}\) یا \(\overline{PQ}\))، بنابراین دیگر سه نقطۀ متمایز که برای ایجاد یک دایره مورد نیاز می باشد را نخواهید داشت.
-
مکان هندسی را ترسیم کنید و آن را با واژگان توصیف نمایید.
شکل 6-20 این مکان هندسی را نشان می دهد، و عنوان آن توصیفش می کند. به نقاط توخالی در \(P\) و \(R\)، که تعیین می کنند آن نقاط بخشی از پاسخ نمی باشند، توجه کنید.
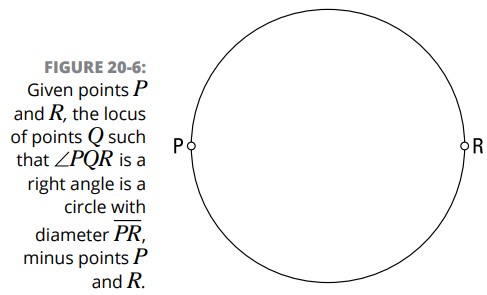
ترجمۀ شکل: با نقاط داده شدۀ \(P\) و \(R\)، مکان هندسی نقاط \(Q\) به نحویکه \(\angle{PQR}\) یک زاویۀ قائمه باشد، دایره ای می باشد که قطر آن \(\overline{PR}\) است، منهای نقاط \(P\) و \(R\).
مسأله های سه بعدی مکان هندسی
در مسأله های سه بعدی مکان هندسی، شما باید مکان هندسی تمامی نقاط را در یک فضای سه بعدی تعیین کنید که شرایط داده شده در مکان هندسی را برآورده می سازند. در این بخش کوتاه، به جای اینکه یک مسالۀ سه بعدی را از آغاز و بدون هیچ داده ای انجام بدهیم، من صرفاً می خواهم در مورد چگونگی مقایسۀ مسأله های سه بعدی مکان هندسی با مسأله های دو بعدی، بحث کنم.
شما می توانید از روش چهار مرحله ای مکان هندسی برای حل کردن مسأله های سه بعدی مکان هندسی نیز مستقیماً استفاده کنید، اما اگر این خیلی مشکل به نظر آید یا اینکه شما گیر کنید، ابتدا سعی کنید که نسخۀ دو بعدی آن مسأله را حل کنید. معمولاً پاسخ دو بعدی به روش پاسخ سه بعدی اشاره می کند. در اینجا این ارتباط را داریم:
-
پاسخ های سه بعدی اغلب (و نه همیشه) می توانند از روی یک پاسخ دو بعدی بوسیلۀ چرخاندن یک پاسخ دو بعدی پیرامون برخی خط ها، بدست آیند. (اغلب این خط از میان برخی یا همۀ نقطه های داده شده عبور می کند.)
-
پاسخ به یک نسخۀ دو بعدی از یک مسالۀ سه بعدی مکان هندسی همواره یک بُرش از پاسخ مسالۀ سه بعدی می باشد (از این جهت یک برش می باشد که یک دایره یک برش از یک کُره می باشد، یا به عبارت دیگر یک دایره تقاطع یک صفحه و یک کره می باشد.)
برای اینکه درک واضحی از این نکتۀ سه بعدی داشته باشید، نگاهی به نسخۀ سه بعدی مسأله های سه بعدی مکان هندسی که در بخشهای پیشین مطرح شدند، بیندازید (من برای اینکه آنها را طبق ترتیب اصلیشان ذکر نکرده ام دلایلی دارم).
نسخۀ سه بعدی مسالۀ دو
به شکل 4-20 ، که پاسخ مسالۀ دو را به شما نشان می دهد، باز گردید. همان مسأله را در نظر بگیرید، اما آن را یک مسالۀ سه بعدی کنید: مکان هندسی نقاطی در یک فضای سه بعدی که از دو نقطۀ داده شده متساوی الفاصله می باشند، چیست؟
پاسخ (به جای یک خط) یک صفحه می باشد که آن صفحه عمود منصف پاره خطی که این دو نقطه را به یکدیگر متصل کرده است، می باشد. در مورد این پاسخ به چند چیز توجه کنید:
-
شما می توانید با چرخاندن پاسخ دو بعدی (خط عمود منصف) پیرامون \(\overleftrightarrow{AB}\)، یعنی خطی که از میان این دو نقطۀ داده شده عبور می کند، به پاسخ سه بعدی (صفحۀ عمود منصف) دست یابید.
-
این پاسخ دو بعدی یک برش از پاسخ سه بعدی می باشد. اینکه این پاسخ دو بعدی را یک برش بنامیم ممکن است عجیب به نظر آید، اما اگر شما پاسخ سه بعدی (یک صفحه) را با یک صفحۀ دیگر برش دهید، به یک خط می رسید.
اکنون نسخۀ اصلاح شدۀ مسالۀ دو را در نظر بگیرید. پاسخ آن را ممکن است بیاد بیاورید، که با پاسخ مسالۀ دو یکسان می باشد (یک عمود منصف)، اما با دو نقطۀ اضافه شده و یک نقطۀ حذف شده. این پاسخ دو بعدی در بصری سازی پاسخ سه بعدی به شما کمک می کند. پاسخ نسخۀ سه بعدی برابر با پاسخ نسخۀ دو بعدی که پیرامون \(\overleftrightarrow{AB}\) چرخانده شده است، می باشد، یعنی صفحۀ عمود منصف، بعلاوۀ نقاط \(A\) و \(B\) ، منهای نقطۀ میانی \(\overline{AB}\) .
نسخۀ سه بعدی مسالۀ سه
نسخۀ سه بعدی مسالۀ سه (با نقطه های داده شدۀ \(P\) و \(R\)، مکان هندسی نقاط \(Q\) در فضا به نحویکه \(\angle{PQR}\) یک زاویۀ قائمه باشد، چیست؟) مسالۀ دیگری است که می توانید پاسخ سه بعدی را با چرخاندن پاسخ دو بعدی بدست آورید. شکل 6-20 که پیشتر نشان داده شد، این پاسخ دو بعدی را نشان داده و همینطور توصیف می کند: آن یک دایره منهای نقاط پایانی قطر \(\overline{PR}\) می باشد. اگر این پاسخ دو بعدی را پیرامون \(\overleftrightarrow{PR}\) بچرخانید، پاسخ سه بعدی را بدست می آورید: پاسخ یک کره با قطر \(\overline{PR}\)، منهای نقاط \(P\) و \(R\) می باشد.
نسخۀ سه بعدی مسالۀ یک
شکل 2-20 که پیشتر نشان داده شد، پاسخ مسالۀ یک را نشان داده و توصیف می کند: دو دایرۀ متحدالمرکز. اما برخلاف سایر مسأله های سه بعدی در این بخش، پاسخ نسخۀ سه بعدی این مسأله (مکان هندسی تمامی نقاطی در فضا که سه واحد از دایرۀ داده شده با شعاع 10 واحد، فاصله دارند، چه می باشد؟) نمی تواند با چرخاندن پاسخ دو بعدی بدست آید. اگرچه، این پاسخ دو بعدی هنوز هم می تواند در تجسم کردن پاسخ سه بعدی به شما کمک کند، زیرا این پاسخ دو بعدی یک برش از پاسخ سه بعدی می باشد. آیا می توانید پاسخ سه بعدی را تجسم کنید؟ این پاسخ سه بعدی شکل یک دونات (donut) را دارد ـــ به زبان ریاضی به این شکل چنبره (torus) گفته می شود ـــ که عرض آن \(26\) واحد و عرض سوراخ آن \(14\) واحد می باشد. تجسم کنید که این دونات را به یک دستگاه برش نان شیرینی حلقوی (bagel slicer) برش زده اید. سطح مسطح هر کدام از این نصفه دونات ها یک دایرۀ کوچک در محل سوراخ دونات و یک دایرۀ بزرگ پیرامون لبۀ بیرونی دارد. به دو دایرۀ پررنگ در شکل 2-20 برگردید. آنها دو دایره ای را که در نصف دونات می بینید به شما نشان می دهند.
یادداشت مترجم: برای اینکه درکی از دستگاه برش نان شیرینی حلقوی (bagel slicer) پیدا کنید تصویر آن را در اینجا آورده ایم.


لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: