خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
درک زبان مثلثات

هر موضوع ریاضی یا علمی دارای واژگان منحصر به فرد خودش می باشد. برخی از کلمات بسیار زیبای روزمره هنگامی که در محتوی آن موضوع مورد استفاده قرار می گیرند معانی جدید و خاصی را می یابند. مثلثات از این قاعده مستثنی نمی باشد.

هر مثلث دارای شش بخش می باشد: سه ضلع و سه زاویه. اگر اضلاع آن را اندازه گیری کنید و سپس آن اندازه گیری ها را با یکدیگر جفت کنید (هر بار دو تا از آنها را بگیرید)، سه جفت متفاوت خواهید داشت. با این جفت ها مسأله های تقسیم را انجام بدهید ـــ ترتیب هر جفت را تغییر بدهید ـــ و شش پاسخ متفاوت خواهید داشت. این شش پاسخ متفاوت نشان دهندۀ شش تابع مثلثاتی خواهند بود. به عنوان مثال، اگر مثلث شما دارای اضلاعی با اندازه های \(3\)، \(4\)، و \(5\) باشد، سپس این شش تقسیم عبارت از \(\frac{3}{4}\)، \(\frac{4}{3}\)، \(\frac{3}{5}\)، \(\frac{5}{3}\) ، \(\frac{4}{5}\) ، و \(\frac{5}{4}\) خواهند بود.
در فصل 7، شما درخواهید یافت چگونه تمامی این کسرها با استفاده از اضلاع متفاوت از یک زاویۀ قائمه، در دنیای توابع مثلثاتی کار می کنند. و سپس، در فصل 8، با کشف اینکه چگونه این توابع مثلثاتی را با یک دایره تعریف کنید، به رویکرد کاملاً متفاوت می رسید.
اسامی این شش تابع مثلثاتی سینوس (sine)، کسینوس (cosine)، تانژانت (tangent)، کتانژانت (cotangent)، سکانت (secant)، و کسکانت (cosecant) می باشند.
هرچند کلمۀ sine (سینوس) زیاد طولانی نیست، شما یک مخفف سه حرفی برای این تابع مثلثاتی و همچنین سایر آنها دارید. ریاضیدانان دریافته اند که استفاده از نسخه های مخفف شده ساده تر می باشد، و آن نسخه ها بر روی دکمه های ماشین حساب بهتر جای می گیرند.
همانطور که می بینید، به جز مورد cosecant، در سایر موارد سه حرف اول کلمۀ اصلی برابر با مخفف شدۀ آن می باشد.
تمرکز اصلی در مثلثات بر روی زوایا می باشد، و حتی اگر اندازۀ آنها را ندانید می توانید با آنها کار کنید. بسیاری از زوایا و اندازۀ آن زوایا دارای قوانین عمومی که بر آنها اعمال می گردد، می باشند. شما می توانید زوایا را با یک حرف، سه حرف، یا یک عدد نامگذاری کنید، اما برای حل کردن مسأله های مثلثات و محاسبات آنها، ریاضیدانان معمولاً به زوایا و اندازه های آنها با حروف الفبای یونانی اشاره می کنند.
رایج ترین حروف الفبای یونانیِ مورد استفاده برای اندازۀ زوایا عبارت از \(\alpha (\text{alpha})\)، \(\beta (\text{beta})\) ، \(\gamma (\text{gamma})\) ، \(\theta (\text{theta})\) می باشند. همچنین، بسیاری از معادلات از متغیر \(x\) برای نشان دادن اندازۀ یک زاویه استفاده می کنند.

ترجمۀ جدول 1-1 : چگونه از بالانویس ها در مثلثات استفاده می کنید
اولین ورودی در جدول 1-1 نشان می دهد چگونه می توانید هربار که می خواهید یک تابع مثلثاتی را به یک توان برسانید ، در نوشتن پرانتزهایی که نیاز به نگارش دارند، صرفه جویی کنید. این نشان گذاری شسته و رفته و کارآمد می باشد، اما اگر شما قانون آن را ندانید ممکن است گیج کننده باشد. دومین ورودی چگونگی نگارش معکوس یک تابع مثلثاتی را به شما نشان می دهد. این بدین معنا می باشد که شما باید مقدار این تابع را بدست آورید و عدد 1 را بر آن تقسیم کنید. آخرین ورودی در جدول 1-1 چگونگی نگارش معکوس تابع سینوس را به شما نشان می دهد. استفاده از بالانویس \(-1\) بین سینوس و زاویه بدین معنا می باشد که شما مشغول صحبت در مورد سینوس معکوس (آرک سینوس: arcsin) ، و نه معکوس این تابع، هستید. در فصل 15، معکوس توابع مثلثاتی را با جزئیات کامل پوشش خواهم داد، تا این موضوع مرتبط با نشان گذاری یک معکوس تابع مثلثاتی شفاف تر گردد.
توابع در جبر از بسیاری از عملگرها و نمادها که متفاوت از علائم رایج جمع، تفریق، ضرب، و تقسیم در حساب می باشند، استفاده می کنند. به عنوان مثال، نگاهی به عملیات جذر \(\sqrt{25}=5\) بیندازید. قرار دادن \(25\) زیر رادیکال (نماد جذر) منجر به تولید پاسخ \(5\) می شود. سایر عملیات ها در جبر، مانند قدر مطلق، فاکتوریل، و تابع پله ای، در مثلثات نیز مورد استفاده قرار می گیرند. اما دنیای مثلثات با تولید فرآیندهای هیجان انگیز بیشتر، این افق فکری را گسترش می دهد. هنگام کار با توابع مثلثاتی، شما یک مجموعۀ جدید کامل از مقادیر برای یادگیری یا پیدا کردن دارید. به عنوان مثال، قرار دادن \(25\) درون تابع سینوس شبیه این می باشد: \(\sin 25\) . پاسخی که از آن بیرون می آید، بسته به اینکه شما درجه یا رادیان را استفاده می کنید، برابر با \(0.423\) و یا برابر با \(-0.132\) است (برای اطلاعات بیشتر در مورد این دو مفهوم مهم مثلثاتی فصل های 4 و 5 را ببینید). شما معمولاً نمی توانید تمامی مقادیری که با قرار دادن اندازۀ زوایا در توابع مثلثاتی بدست می آورید، تعیین کنید یا به حافظه بسپارید. بنابراین برای مطالعۀ مثلثات، نیاز به مقادیر جداول مثلثاتی یا ماشین حساب های علمی دارید.
به طور کلی، هنگامی که یک تابع مثلثاتی را بر روی اندازۀ یک زاویه بکار می گیرید، اعداد حقیقی را بدست می آورید (اگر آن زاویه در دامنۀ آن باشد). برخی از زوایا و توابع مثلثاتی مقادیر زیبایی دارند، اما بیشتر آنها اینطور نیستند. جدول 2-1 توابع مثلثاتی برای یک زاویۀ \(30\) درجه را نشان می دهد.
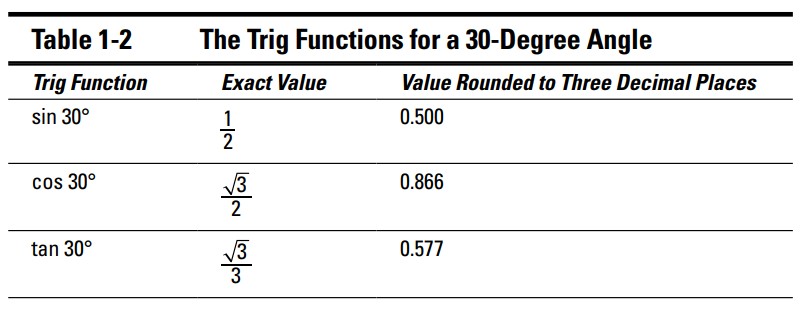

برخی از ویژگیهایی که ورودیهای جدول 2-1 تصدیق می کنند اینست که توابع سینوس و کسینوس همواره دارای مقادیری بین \(-1\) و \(1\) می باشند. همچنین، توابع سکانت و کسکانت همواره دارای مقادیری برابر با یا بزرگتر از \(1\) یا برابر با یا کوچکتر از \(-1\) می باشند. (در فصل 7 در مورد جزئیات این ویژگی ها مفصل بحث خواهم کرد.)
با استفاده از جدول پیوست، این کتاب، می توانید مقادیر بیشتری از توابع مثلثاتی را برای اندازۀ زوایای خاص (در واحد درجه) بیابید:
$$
\tan 45^{\circ} = 1 \\
\csc 90^{\circ} = 1 \\
\sec 60^{\circ} = 2
$$
رادیکال (radical) یک نماد ریاضی بدین معنا می باشد: "عددی را بیابید که یک بار یا بیشتر در خودش ضرب می شود تا مقدار زیر رادیکال را به شما بدهد." شما می بینید که چرا از نمادی همچون \(\sqrt{}\) به جای اینهمه تفسیر استفاده می کنند. رادیکال ها مقادیر توابعی را که به وفور در مثلثات مورد استفاده قرار می گیرند، نشان می دهند. در فصل 7، توابع مثلثاتی را با استفاده از یک مثلث قائم الزاویه تعریف کرده ام. برای بدست آوردن طول اضلاع یک مثلث قائم الزاویه با استفاده از قضیۀ فیثاغورث، شما باید برخی جذرها را محاسبه کنید، که از رادیکال ها استفاده می کنند. برخی پاسخهای ساده به عبارت های رادیکال بدین شرح می باشند: \(\sqrt{16}=4\) ، \(\sqrt{121}=11\) ، \(\sqrt[3]{8}=2\) ، و \(\sqrt[4]{81}=3\) .
این مثالها همگی مربع کامل، مکعب کامل، یا ریشۀ چهارم کامل می باشند، که بدین معنا است که پاسخ عددی است که خاتمه می یابد ـــ بخش اعشاریِ آن تا ابد ادامه نمی یابد. بخش زیر در مورد روشی برای ساده سازی رادیکال هایی که ریشۀ کامل نیستند، بحث می کند.
ساده سازی یک شکل رادیکال بدین معنا می باشد که آن را با عددی کوچکتر در زیر رادیکال بازنویسی کنید ـــ البته اگر شدنی باشد. شما تنها در صورتی می توانید این شکل را ساده سازی کنید که عدد زیر رادیکال دارای یک مربع کامل یا مکعب کامل (یا هر فاکتور کامل دیگر) باشد، که شما بتوانید آن را فاکتور بگیرید.
مثال: \(\sqrt{80}\) را ساده سازی کنید.
عدد \(80\) یک مربع کامل نمی باشد، اما یکی از فاکتورهای آن، \(16\)، مربع کامل است. شما می توانید عدد \(80\) را به شکل حاصلضرب \(16\) و \(5\) بنویسید، این دو رادیکال را جداگانه بنویسید، و سپس هر رادیکال را ارزیابی کنید. حاصلضرب بدست آمده، شکل ساده سازی شده می باشد:
$$\sqrt{80}=\sqrt{16 \cdot 5}=\sqrt{16}\sqrt{5}=4\sqrt{5}$$
مثال: \(\sqrt[3]{250}\) را ساده سازی کنید.
عدد \(250\) یک مکعب کامل نیست، اما یکی از فاکتورهای آن، \(125\)، اینگونه است. \(250\) را به شکل حاصلضرب \(125\) در \(2\) بنویسید: جداسازی کنید، ارزیابی کنید، و حاصلضرب ساده سازی شده را بنویسید:
$$\sqrt[3]{250}=\sqrt[3]{125 \cdot 2}=\sqrt[3]{125}\sqrt[3]{2}=5\sqrt[3]{2}$$
به همان اندازه که رادیکال ساده سازی شده فوق العاده است، و به همان اندازه که در هنگام انجام محاسبات ریاضی بیشتر، مفید است، گاهی اوقات شما صرفاً نیاز دارید تا بدانید مقدار آن چقدر است.
تقریب زدن (Approximating) یک پاسخ بدین معنا است که مقدار واقعی را به لحاظ ارقام اعشار کوتاهتر کنید. علی الخصوص تقریب زدن در مواقعی که مقدار اعشاری یک عدد بدون هیچ الگوی تکراری تا ابد ادامه می یابد، بسیار سودمند می باشد. هنگامی که یک پاسخ را تقریب می زنید، آن را به تعداد خاصی از ارقام اعشار، گرد (round) می کنید و بقیۀ مقادیر اعشاری آن را رها می کنید. اگرچه، قبل از انجام این کار، باید در نظر بگیرید که مقداری که حذف می کنید، چقدر بزرگ است. اگر اعدادی که حذف می کنید با یک \(5\) یا عدد بزرگتر آغاز گردد، آن گاه آخرین رقمی را که نگه داشته اید \(1\) واحد بالا ببرید. اگر چیزی که حذف می کنید با یک \(4\) یا کمتر آغاز می شود، آن گاه صرفاً آخرین رقم باقیمانده را همانطور دست نخورده باقی بگذارید.
مثال: عدد \(3.141592654\) را تا چهار رقم اعشار، سه رقم اعشار، و دو رقم اعشار گرد کنید.
هنگام تقریب زدن مقادیر رادیکال ها از این تکنیک استفاده کنید. با استفاده از یک ماشین حساب، مقدار اعشاری \(\sqrt{80}\) در حدود \(8.94427191\) خواهد بود. بسته به اینکه این مقدار را به چه منظوری مورد استفاده قرار می دهید، ممکن است بخواهید آن را تا دو، سه، چهار، یا بیشتر، ارقام اعشاری گرد کنید. به عنوان مثال اگر این عدد را تا سه رقم اعشار گرد کنید به \(8.944\) می رسید.

معرفی توابع مثلثاتی
هر مثلث دارای شش بخش می باشد: سه ضلع و سه زاویه. اگر اضلاع آن را اندازه گیری کنید و سپس آن اندازه گیری ها را با یکدیگر جفت کنید (هر بار دو تا از آنها را بگیرید)، سه جفت متفاوت خواهید داشت. با این جفت ها مسأله های تقسیم را انجام بدهید ـــ ترتیب هر جفت را تغییر بدهید ـــ و شش پاسخ متفاوت خواهید داشت. این شش پاسخ متفاوت نشان دهندۀ شش تابع مثلثاتی خواهند بود. به عنوان مثال، اگر مثلث شما دارای اضلاعی با اندازه های \(3\)، \(4\)، و \(5\) باشد، سپس این شش تقسیم عبارت از \(\frac{3}{4}\)، \(\frac{4}{3}\)، \(\frac{3}{5}\)، \(\frac{5}{3}\) ، \(\frac{4}{5}\) ، و \(\frac{5}{4}\) خواهند بود.
در فصل 7، شما درخواهید یافت چگونه تمامی این کسرها با استفاده از اضلاع متفاوت از یک زاویۀ قائمه، در دنیای توابع مثلثاتی کار می کنند. و سپس، در فصل 8، با کشف اینکه چگونه این توابع مثلثاتی را با یک دایره تعریف کنید، به رویکرد کاملاً متفاوت می رسید.
اسامی این شش تابع مثلثاتی سینوس (sine)، کسینوس (cosine)، تانژانت (tangent)، کتانژانت (cotangent)، سکانت (secant)، و کسکانت (cosecant) می باشند.
خلاصه نویسی توابع مثلثاتی
هرچند کلمۀ sine (سینوس) زیاد طولانی نیست، شما یک مخفف سه حرفی برای این تابع مثلثاتی و همچنین سایر آنها دارید. ریاضیدانان دریافته اند که استفاده از نسخه های مخفف شده ساده تر می باشد، و آن نسخه ها بر روی دکمه های ماشین حساب بهتر جای می گیرند.
مخفف شدۀ توابع مثلثاتی به شرح زیر می باشند:
-
sine: sin
-
cosine: cos
-
tangent: tan
-
cotangent: cot
-
secant: sec
-
cosecant: csc
همانطور که می بینید، به جز مورد cosecant، در سایر موارد سه حرف اول کلمۀ اصلی برابر با مخفف شدۀ آن می باشد.
نشان گذاریها
تمرکز اصلی در مثلثات بر روی زوایا می باشد، و حتی اگر اندازۀ آنها را ندانید می توانید با آنها کار کنید. بسیاری از زوایا و اندازۀ آن زوایا دارای قوانین عمومی که بر آنها اعمال می گردد، می باشند. شما می توانید زوایا را با یک حرف، سه حرف، یا یک عدد نامگذاری کنید، اما برای حل کردن مسأله های مثلثات و محاسبات آنها، ریاضیدانان معمولاً به زوایا و اندازه های آنها با حروف الفبای یونانی اشاره می کنند.
رایج ترین حروف الفبای یونانیِ مورد استفاده برای اندازۀ زوایا عبارت از \(\alpha (\text{alpha})\)، \(\beta (\text{beta})\) ، \(\gamma (\text{gamma})\) ، \(\theta (\text{theta})\) می باشند. همچنین، بسیاری از معادلات از متغیر \(x\) برای نشان دادن اندازۀ یک زاویه استفاده می کنند.
نکات فنی: جبر دارای نماد قراردادی بالانویس ها، مانند \(2\) در \(x^2\) می باشد. در مثلثات، بالانویس ها دارای قواعد و ویژگی های یکسانی مشابه سایر ریاضیات می باشند. اما بالانویس های مثلثات اغلب بسیار متفاوت به نظر می رسند. جدول 1-1 لیستی از چندین روش که مثلثات از این بالانویس ها استفاده می کند به شما نشان می دهد.

ترجمۀ جدول 1-1 : چگونه از بالانویس ها در مثلثات استفاده می کنید
|
چگونگی نگارش در مثلثات |
نشان گذاری جایگزین |
معنای بالانویس |
|---|---|---|
|
\(\sin^2 \theta\) |
\((\sin \theta)^2\) |
سینوس زاویۀ تتا را مربع سازید |
|
\((\sin \theta)^{-1}\) |
\(\frac{1}{\sin \theta}\) |
معکوس سینوس تتا را بیابید |
|
\(\sin^{-1} \theta\) |
\(\arcsin \theta\) |
زاویۀ تتا که سینوس آن داده شده است را بیابید |
اولین ورودی در جدول 1-1 نشان می دهد چگونه می توانید هربار که می خواهید یک تابع مثلثاتی را به یک توان برسانید ، در نوشتن پرانتزهایی که نیاز به نگارش دارند، صرفه جویی کنید. این نشان گذاری شسته و رفته و کارآمد می باشد، اما اگر شما قانون آن را ندانید ممکن است گیج کننده باشد. دومین ورودی چگونگی نگارش معکوس یک تابع مثلثاتی را به شما نشان می دهد. این بدین معنا می باشد که شما باید مقدار این تابع را بدست آورید و عدد 1 را بر آن تقسیم کنید. آخرین ورودی در جدول 1-1 چگونگی نگارش معکوس تابع سینوس را به شما نشان می دهد. استفاده از بالانویس \(-1\) بین سینوس و زاویه بدین معنا می باشد که شما مشغول صحبت در مورد سینوس معکوس (آرک سینوس: arcsin) ، و نه معکوس این تابع، هستید. در فصل 15، معکوس توابع مثلثاتی را با جزئیات کامل پوشش خواهم داد، تا این موضوع مرتبط با نشان گذاری یک معکوس تابع مثلثاتی شفاف تر گردد.
کار کردن با زاویه ها
توابع در جبر از بسیاری از عملگرها و نمادها که متفاوت از علائم رایج جمع، تفریق، ضرب، و تقسیم در حساب می باشند، استفاده می کنند. به عنوان مثال، نگاهی به عملیات جذر \(\sqrt{25}=5\) بیندازید. قرار دادن \(25\) زیر رادیکال (نماد جذر) منجر به تولید پاسخ \(5\) می شود. سایر عملیات ها در جبر، مانند قدر مطلق، فاکتوریل، و تابع پله ای، در مثلثات نیز مورد استفاده قرار می گیرند. اما دنیای مثلثات با تولید فرآیندهای هیجان انگیز بیشتر، این افق فکری را گسترش می دهد. هنگام کار با توابع مثلثاتی، شما یک مجموعۀ جدید کامل از مقادیر برای یادگیری یا پیدا کردن دارید. به عنوان مثال، قرار دادن \(25\) درون تابع سینوس شبیه این می باشد: \(\sin 25\) . پاسخی که از آن بیرون می آید، بسته به اینکه شما درجه یا رادیان را استفاده می کنید، برابر با \(0.423\) و یا برابر با \(-0.132\) است (برای اطلاعات بیشتر در مورد این دو مفهوم مهم مثلثاتی فصل های 4 و 5 را ببینید). شما معمولاً نمی توانید تمامی مقادیری که با قرار دادن اندازۀ زوایا در توابع مثلثاتی بدست می آورید، تعیین کنید یا به حافظه بسپارید. بنابراین برای مطالعۀ مثلثات، نیاز به مقادیر جداول مثلثاتی یا ماشین حساب های علمی دارید.
به طور کلی، هنگامی که یک تابع مثلثاتی را بر روی اندازۀ یک زاویه بکار می گیرید، اعداد حقیقی را بدست می آورید (اگر آن زاویه در دامنۀ آن باشد). برخی از زوایا و توابع مثلثاتی مقادیر زیبایی دارند، اما بیشتر آنها اینطور نیستند. جدول 2-1 توابع مثلثاتی برای یک زاویۀ \(30\) درجه را نشان می دهد.


برخی از ویژگیهایی که ورودیهای جدول 2-1 تصدیق می کنند اینست که توابع سینوس و کسینوس همواره دارای مقادیری بین \(-1\) و \(1\) می باشند. همچنین، توابع سکانت و کسکانت همواره دارای مقادیری برابر با یا بزرگتر از \(1\) یا برابر با یا کوچکتر از \(-1\) می باشند. (در فصل 7 در مورد جزئیات این ویژگی ها مفصل بحث خواهم کرد.)
با استفاده از جدول پیوست، این کتاب، می توانید مقادیر بیشتری از توابع مثلثاتی را برای اندازۀ زوایای خاص (در واحد درجه) بیابید:
$$
\tan 45^{\circ} = 1 \\
\csc 90^{\circ} = 1 \\
\sec 60^{\circ} = 2
$$
من این چند مثال را به این دلیل انتخاب کردم که پاسخهای آنها زیبا و کامل بودند. بیشتر زوایا و بیشتر توابع بسیار نامرتب تر از این مثال ها به نظر می رسند.
رادیکال ها
رادیکال (radical) یک نماد ریاضی بدین معنا می باشد: "عددی را بیابید که یک بار یا بیشتر در خودش ضرب می شود تا مقدار زیر رادیکال را به شما بدهد." شما می بینید که چرا از نمادی همچون \(\sqrt{}\) به جای اینهمه تفسیر استفاده می کنند. رادیکال ها مقادیر توابعی را که به وفور در مثلثات مورد استفاده قرار می گیرند، نشان می دهند. در فصل 7، توابع مثلثاتی را با استفاده از یک مثلث قائم الزاویه تعریف کرده ام. برای بدست آوردن طول اضلاع یک مثلث قائم الزاویه با استفاده از قضیۀ فیثاغورث، شما باید برخی جذرها را محاسبه کنید، که از رادیکال ها استفاده می کنند. برخی پاسخهای ساده به عبارت های رادیکال بدین شرح می باشند: \(\sqrt{16}=4\) ، \(\sqrt{121}=11\) ، \(\sqrt[3]{8}=2\) ، و \(\sqrt[4]{81}=3\) .
این مثالها همگی مربع کامل، مکعب کامل، یا ریشۀ چهارم کامل می باشند، که بدین معنا است که پاسخ عددی است که خاتمه می یابد ـــ بخش اعشاریِ آن تا ابد ادامه نمی یابد. بخش زیر در مورد روشی برای ساده سازی رادیکال هایی که ریشۀ کامل نیستند، بحث می کند.
ساده سازیِ شکلهای رادیکال
ساده سازی یک شکل رادیکال بدین معنا می باشد که آن را با عددی کوچکتر در زیر رادیکال بازنویسی کنید ـــ البته اگر شدنی باشد. شما تنها در صورتی می توانید این شکل را ساده سازی کنید که عدد زیر رادیکال دارای یک مربع کامل یا مکعب کامل (یا هر فاکتور کامل دیگر) باشد، که شما بتوانید آن را فاکتور بگیرید.
مثال: \(\sqrt{80}\) را ساده سازی کنید.
عدد \(80\) یک مربع کامل نمی باشد، اما یکی از فاکتورهای آن، \(16\)، مربع کامل است. شما می توانید عدد \(80\) را به شکل حاصلضرب \(16\) و \(5\) بنویسید، این دو رادیکال را جداگانه بنویسید، و سپس هر رادیکال را ارزیابی کنید. حاصلضرب بدست آمده، شکل ساده سازی شده می باشد:
$$\sqrt{80}=\sqrt{16 \cdot 5}=\sqrt{16}\sqrt{5}=4\sqrt{5}$$
مثال: \(\sqrt[3]{250}\) را ساده سازی کنید.
عدد \(250\) یک مکعب کامل نیست، اما یکی از فاکتورهای آن، \(125\)، اینگونه است. \(250\) را به شکل حاصلضرب \(125\) در \(2\) بنویسید: جداسازی کنید، ارزیابی کنید، و حاصلضرب ساده سازی شده را بنویسید:
$$\sqrt[3]{250}=\sqrt[3]{125 \cdot 2}=\sqrt[3]{125}\sqrt[3]{2}=5\sqrt[3]{2}$$
تقریب زدن پاسخها
به همان اندازه که رادیکال ساده سازی شده فوق العاده است، و به همان اندازه که در هنگام انجام محاسبات ریاضی بیشتر، مفید است، گاهی اوقات شما صرفاً نیاز دارید تا بدانید مقدار آن چقدر است.
تقریب زدن (Approximating) یک پاسخ بدین معنا است که مقدار واقعی را به لحاظ ارقام اعشار کوتاهتر کنید. علی الخصوص تقریب زدن در مواقعی که مقدار اعشاری یک عدد بدون هیچ الگوی تکراری تا ابد ادامه می یابد، بسیار سودمند می باشد. هنگامی که یک پاسخ را تقریب می زنید، آن را به تعداد خاصی از ارقام اعشار، گرد (round) می کنید و بقیۀ مقادیر اعشاری آن را رها می کنید. اگرچه، قبل از انجام این کار، باید در نظر بگیرید که مقداری که حذف می کنید، چقدر بزرگ است. اگر اعدادی که حذف می کنید با یک \(5\) یا عدد بزرگتر آغاز گردد، آن گاه آخرین رقمی را که نگه داشته اید \(1\) واحد بالا ببرید. اگر چیزی که حذف می کنید با یک \(4\) یا کمتر آغاز می شود، آن گاه صرفاً آخرین رقم باقیمانده را همانطور دست نخورده باقی بگذارید.
مثال: عدد \(3.141592654\) را تا چهار رقم اعشار، سه رقم اعشار، و دو رقم اعشار گرد کنید.
-
چهار رقم اعشار (Four decimal places): این مقدار گرد شده بدین معناست که \(3.141?\) باقی می ماند (علامت سوال آخرین مکان را نگهداری می کند تا اینکه شما تصمیمی برای آن بگیرید). از آنجایی که شما می خواهید \(92654\) را حذف کنید، و اولین رقم از این اعداد حذف شده \(9\) می باشد، آخرین رقم یعنی \(5\) را یک واحد افزایش بدهید تا به \(6\) تبدیل گردد. بنابراین اگر عدد \(3.141592654\) را تا چهار رقم اعشار گرد کنیم به عدد \(3.1416\) می رسیم.
-
سه رقم اعشار (Three decimal places): عدد \(3.14?\) باقی می ماند. از آنجا که شما \(592654\) را حذف می کنید که با \(5\) آغاز شده است، آخرین رقمی را که نگه داشته اید، یعنی \(1\) را، یک واحد افزایش بدهید که تبدیل به \(2\) می گردد. بنابراین اگر عدد \(3.141592654\) را تا سه رقم اعشار گرد کنید به \(3.142\) می رسید.
-
دو رقم اعشار (Two decimal places): عدد \(3.1?\) باقی می ماند. از آنجا که عدد حذف شده، یعنی \(1592654\) با رقم \(1\) آغاز می گردد، آخرین رقمی که حفظش کرده اید، یعنی \(4\) بدون تغییر باقی می ماند. بنابراین اگر عدد \(3.141592654\) را تا دو رقم اعشار گرد کنید به عدد \(3.14\) می رسید.
هنگام تقریب زدن مقادیر رادیکال ها از این تکنیک استفاده کنید. با استفاده از یک ماشین حساب، مقدار اعشاری \(\sqrt{80}\) در حدود \(8.94427191\) خواهد بود. بسته به اینکه این مقدار را به چه منظوری مورد استفاده قرار می دهید، ممکن است بخواهید آن را تا دو، سه، چهار، یا بیشتر، ارقام اعشاری گرد کنید. به عنوان مثال اگر این عدد را تا سه رقم اعشار گرد کنید به \(8.944\) می رسید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (2 دیدگاه)
دیدگاه خود را ثبت کنید: