خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ترسیم نقاط در دستگاه مختصات

یک تصویر به اندازۀ هزاران کلمه می ارزد. ترسیم تصاویر یا نمودارهای توابع و معادلات در ریاضی، در درک چیزی که در جریان است، به شما کمک می کند. در مثلثات، شما اغلب علاوه بر منحنی هایی که نشان دهندۀ توابع مثلثاتی (سینوس، کسینوس، تانژانت، کتانژانت، سکانت، کسکانت) هستند، زوایا و مثلث ها را ترسیم می کنید. دستگاه مختصات دکارتی استاندارد، که در هنگام ترسیم نمودارها در جبر و سایر موضوعات ریاضی مورد استفاده قرار می دادید، در اینجا بهتر کار می کند. اگر به دنبال یک یادآوری در این دستگاه ترسیم نقاط می باشد، می توانید در این فصل آن را بیابید. به طور خلاصه، با دستگاه مختصات دکارتی، همه چیز از چپ به راست و پایین به بالا خوانده می شود، از میان اعداد منفی می گذرند تا به اعداد مثبت برسند.

ترسیم نقاط (Plotting points) در یک نمودار ریاضی بدین معنا می باشد که موقعیت صحیح یک نقطه که با یک جفت مرتب از اعداد، مانند \((2,3)\) ، \((-1,4)\)، یا \((0,0)\) نشان داده شده است، را بیابید. این جفت مرتب \((x,y)\) مختصات دکارتی (Cartesian coordinates) آن نقطه نامیده می شود. شما با دو خط متقاطع که محورها (axes) نامیده می شوند، کار را آغاز می کنید.
ترسیم نقاط و رسم نمودارها به دو محور و یک فاصله یا مقیاس تعریف شده بر روی آنها نیاز دارد. این دو خط متعامد و متقاطع که یک نمودار را می سازند، محورهای افقی و عمودی (یا محورهای مختصات) نامیده می شوند.
این خطها تا ابد به سمت چپ و راست، بالا و پایین، گسترش می یابند. به طور سنتی به محور افقی، محور x گفته می شود، همچنین در مثلثات معمولاً به محور افقی محور \(\theta\) گفته می شود. محور عمودی همان محور y می باشد. این دو محور در نقطه ای که مبدأ (origin) نامیده می شود، یکدیگر را قطع می کنند، که آن را با برچسب \(O\) نشان می دهند. بخشی از محور x که به سمت راست می رود نشان دهندۀ مقادیر عددی مثبت می باشد، و شما از آن به عنوان محل آغاز یا سمت نخستین در هنگام ترسیم زوایا در یک موقعیت استاندارد (standard position)، استفاده می کنید. یک زاویه در موقعیت استاندارد دارای رأسی در مبدأ می باشد، ضلع نخستین آن در امتداد محور x مثبت می باشد، و ضلع پایانی آن یک نیمخط است که در جهت خلاف گردش عقربه های ساعت چرخیده است.
نقطه ای که این دو محور همدیگر را قطع می کنند، مبدأ (origin) نامیده می شود. شما آن را با یک \(O\) و یا با جفت مرتب آن یعنی \((0,0)\) برچسب گذاری می کنید. مبدأ نقطۀ آغاز شمارش مختصات هنگام ترسیم نمودار تمامی نقاط دیگر می باشد. همچنین مبدأ نقطۀ پایانی نیم خطهایی (خطهایی که در یک جهت تا بی نهایت می روند) می باشد که در هنگام ترسیم زوایا در موقعیت استاندارد بر روی محورهای مختصات از آنها استفاده می کنید.
ترسیم نقاط در یک دستگاه مختصات شامل شمارش فاصله ها از مبدأ به سمت راست یا چپ و بالا یا پایین می باشد. این محورها به عنوان یک نقطۀ شروع عمل می کنند. این نقاط که با یک جفت مرتب از اعداد نشان داده می شوند، \((x,y)\) ، مختصات x و مختصات y نامیده می شوند. نامگذاری جفت مرتب (ordered pair) بدین معناست که ترتیب (order) در آن حائز اهمیت می باشد. مختصات x همواره در ابتدا می آید، و مختصات y همیشه در انتها می آید، به نحویکه کل این دستگاه نموداری یک چیز جهانی می باشد.
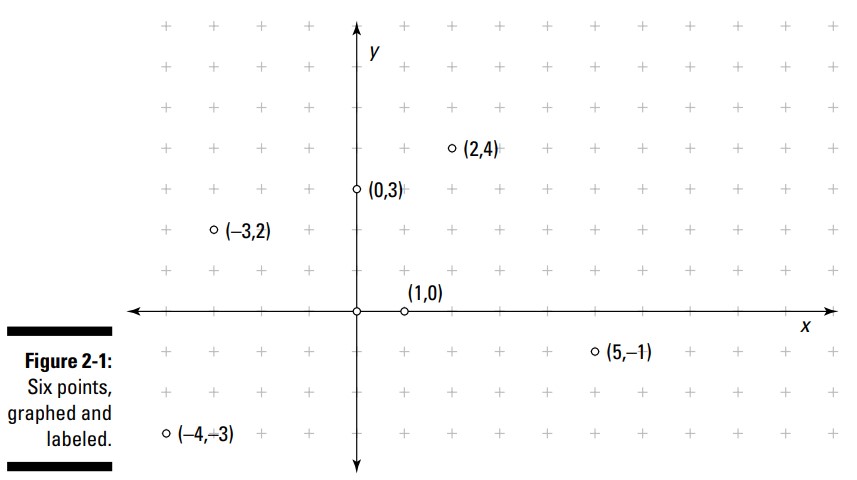
نقطۀ \((2,4)\) از مبدأ دو واحد به سمت راست و چهار واحد به سمت بالا می باشد؛ \((-3,2)\) سه واحد به سمت چپ و دو واحد به سمت بالا می باشد؛ \((-4,-3)\) چهار واحد به سمت چپ و سه واحد به سمت پایین می باشد؛ و \((5,-1)\) پنج واحد به سمت راست و یک واحد به سمت پایین می باشد. همچنی نقاط می توانند بر روی یکی از این محورها نیز قرار بگیرند. نقاطی که بر روی محورها قرار می گیرند همواره دارای مقدار \(0\) برای مختصات x یا مختصات y می باشند. نقطۀ \((0,3)\) بر روی محور y قرار می گیرد، و \((1,0)\) بر روی محور x قرار می گیرد. چگونگی ترسیم تمامی این نقاط را در شکل 1-2 ببینید.
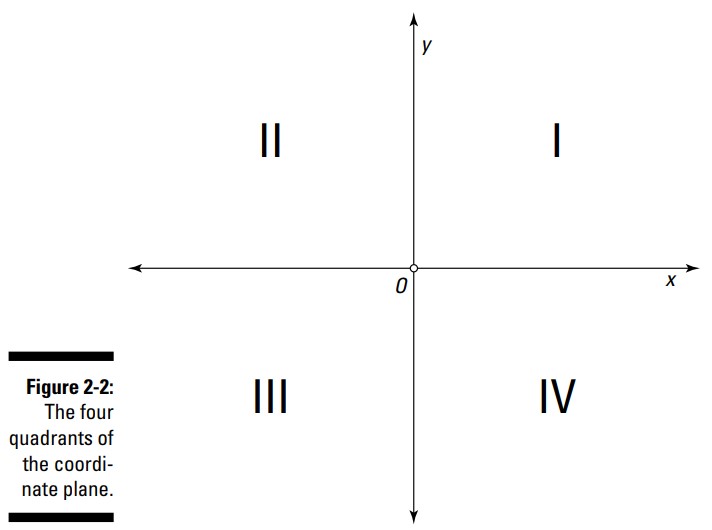
تقاطع محور x و محور y کل تصویر، یا صفحۀ مختصات، را به چهار ناحیۀ جداگانه که رُبع صفحه (quadrants) نامیده می شوند، تقسیم می کند. همانطور که در شکل 2-2 نشان داده شده است، این ربع صفحه ها به ترتیب از ربع صفحۀ بالا و راست و در خلاف جهت گردش عقربه های ساعت، شماره گذاری شده اند. به طور سنتی ربع صفحه ها را با اعداد رومی شماره گذاری می کنند.

ترسیم نقاط
ترسیم نقاط (Plotting points) در یک نمودار ریاضی بدین معنا می باشد که موقعیت صحیح یک نقطه که با یک جفت مرتب از اعداد، مانند \((2,3)\) ، \((-1,4)\)، یا \((0,0)\) نشان داده شده است، را بیابید. این جفت مرتب \((x,y)\) مختصات دکارتی (Cartesian coordinates) آن نقطه نامیده می شود. شما با دو خط متقاطع که محورها (axes) نامیده می شوند، کار را آغاز می کنید.
محورهای مختصات (Axes)
ترسیم نقاط و رسم نمودارها به دو محور و یک فاصله یا مقیاس تعریف شده بر روی آنها نیاز دارد. این دو خط متعامد و متقاطع که یک نمودار را می سازند، محورهای افقی و عمودی (یا محورهای مختصات) نامیده می شوند.
این خطها تا ابد به سمت چپ و راست، بالا و پایین، گسترش می یابند. به طور سنتی به محور افقی، محور x گفته می شود، همچنین در مثلثات معمولاً به محور افقی محور \(\theta\) گفته می شود. محور عمودی همان محور y می باشد. این دو محور در نقطه ای که مبدأ (origin) نامیده می شود، یکدیگر را قطع می کنند، که آن را با برچسب \(O\) نشان می دهند. بخشی از محور x که به سمت راست می رود نشان دهندۀ مقادیر عددی مثبت می باشد، و شما از آن به عنوان محل آغاز یا سمت نخستین در هنگام ترسیم زوایا در یک موقعیت استاندارد (standard position)، استفاده می کنید. یک زاویه در موقعیت استاندارد دارای رأسی در مبدأ می باشد، ضلع نخستین آن در امتداد محور x مثبت می باشد، و ضلع پایانی آن یک نیمخط است که در جهت خلاف گردش عقربه های ساعت چرخیده است.
مبدأ مختصات
نقطه ای که این دو محور همدیگر را قطع می کنند، مبدأ (origin) نامیده می شود. شما آن را با یک \(O\) و یا با جفت مرتب آن یعنی \((0,0)\) برچسب گذاری می کنید. مبدأ نقطۀ آغاز شمارش مختصات هنگام ترسیم نمودار تمامی نقاط دیگر می باشد. همچنین مبدأ نقطۀ پایانی نیم خطهایی (خطهایی که در یک جهت تا بی نهایت می روند) می باشد که در هنگام ترسیم زوایا در موقعیت استاندارد بر روی محورهای مختصات از آنها استفاده می کنید.
ترسیم x در مقایسه با y
ترسیم نقاط در یک دستگاه مختصات شامل شمارش فاصله ها از مبدأ به سمت راست یا چپ و بالا یا پایین می باشد. این محورها به عنوان یک نقطۀ شروع عمل می کنند. این نقاط که با یک جفت مرتب از اعداد نشان داده می شوند، \((x,y)\) ، مختصات x و مختصات y نامیده می شوند. نامگذاری جفت مرتب (ordered pair) بدین معناست که ترتیب (order) در آن حائز اهمیت می باشد. مختصات x همواره در ابتدا می آید، و مختصات y همیشه در انتها می آید، به نحویکه کل این دستگاه نموداری یک چیز جهانی می باشد.
مختصات x فاصلۀ مبدأ تا سمت چپ یا راست، تا محلی که نقطۀ مورد نظر قرار گرفته است، می باشد. اگر مختصات x مثبت باشد، شما به سمت راست مبدأ حرکت می کنید. اگر منفی باشد، به سمت چپ می روید. دومین عدد، مختصات y، مسافتی است که از مبدأ رو به سمت بالا یا پایین می روید. اعداد مثبت به معنای این می باشد که آن نقطه در بالا قرار دارد و منفی ها به معنای این هستند که شما به سمت جنوب محور x حرکت می کنید.
نقطۀ \((2,4)\) از مبدأ دو واحد به سمت راست و چهار واحد به سمت بالا می باشد؛ \((-3,2)\) سه واحد به سمت چپ و دو واحد به سمت بالا می باشد؛ \((-4,-3)\) چهار واحد به سمت چپ و سه واحد به سمت پایین می باشد؛ و \((5,-1)\) پنج واحد به سمت راست و یک واحد به سمت پایین می باشد. همچنی نقاط می توانند بر روی یکی از این محورها نیز قرار بگیرند. نقاطی که بر روی محورها قرار می گیرند همواره دارای مقدار \(0\) برای مختصات x یا مختصات y می باشند. نقطۀ \((0,3)\) بر روی محور y قرار می گیرد، و \((1,0)\) بر روی محور x قرار می گیرد. چگونگی ترسیم تمامی این نقاط را در شکل 1-2 ببینید.

بریدن نمودار به چهار بخش
تقاطع محور x و محور y کل تصویر، یا صفحۀ مختصات، را به چهار ناحیۀ جداگانه که رُبع صفحه (quadrants) نامیده می شوند، تقسیم می کند. همانطور که در شکل 2-2 نشان داده شده است، این ربع صفحه ها به ترتیب از ربع صفحۀ بالا و راست و در خلاف جهت گردش عقربه های ساعت، شماره گذاری شده اند. به طور سنتی ربع صفحه ها را با اعداد رومی شماره گذاری می کنند.
این نامگذاری ربع صفحه ها هنگامی که به برخی از انواع خاص زوایا، گروه بندی نقاط، و ویژگیهای توابع مثلثاتی، اشاره می کنید، سودمند هستند. نقاطی که در ربع \(I\) قرار دارند، همگی دارای مختصات x و مختصات y مثبت می باشند. در ربع صفحۀ \(II\) ، مختصات x منفی، و مختصات y مثبت می باشند. نقاط قرار گرفته در ربع صفحۀ \(III\) دارای مختصات x و y منفی می باشند. در ربع صفحۀ \(IV\) ، مختصات x مثبت، و مختصات y منفی می باشد.

لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: