خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توابع مثلثاتی: سینوس، کسینوس، و تانژانت
اجداد ما با گرفتن طول اضلاع یک مثلث قائم الزاویه یا وترهای دایره ها و ایجاد نسبت هایی با آن اعداد و متغیرها، تولد توابع مثلثاتی را رقم زدند. این توابع بی نهایت ارزشمند هستند، زیرا به شما امکان می دهند تا از ستاره ها برای ناوبری استفاده کنید و پل هایی بسازید که سقوط نمی کنند. اگر شما هرگز با ناوبری یک قایق یا مهندسی درگیر نبوده اید، در اینصورت می توانید از توابع مثلثاتی در خانه برای توسعۀ ساختمان استفاده کنید. برای دانش آموزانی که قصد دارند وارد دورۀ حسابان (calculus) گردند، توابع مثلثاتی جزء اصلی و اساسی می باشند.

این شش تابع مثلثاتی یک چیز را از شما تقاضا می کنند ـــ وارد کردن اندازۀ یک زاویه ـــ و سپس عددی را به عنوان خروجی به شما می دهند. این خروجی ها می توانند هر عدد حقیقی، از بی نهایت کوچک تا بی نهایت بزرگ و هر چیز دیگری بین آنها، باشند. نتایجی که دریافت می کنید بستگی به تابع مثلثاتی مورد استفاده دارد. اگرچه برخی از محاسبات اولیه نسبتاً خسته کننده بودند، امروزه ماشین حسابهای دستی همه چیز را بسیار ساده تر کرده اند.
SohCahToa کیست یا چیست؟ شاید یک نوع پاستای ایتالیایی، شاید یک پرنسس بومی آمریکایی، یا شاید دارویی معجزه آور باشد؟ در واقع هیچکدام از اینها نیست. بعضی از معلم های ریاضی باهوش این واژه را اختراع کرده اند تا در یادآوری نسبت های مثلثاتی به دانش آموزان کمک کند. بعد از آن بود که این کلمه در همه جا پخش شد. قبل از اینکه به شما توضیح بدهم SohCahToa چیست، باید بدانید که این حروف مخفف چه چیزهایی هستند. حروف بزرگ \(S\)، \(C\)، و \(T\) به ترتیب مخفف توابع مثلثاتی sine (سینوس)، cosine (کسینوس)، و tangent (تانژانت) می باشند. حروف کوچک نسبتهای آنها را در یک مثلث قائم الزاویه نشان می دهند.
یک مثلث قائم الزاویه دو ضلع کوتاهتر، یا دو ساق، دارد و بلندترین ضلع، مقابل زاویۀ قائمه است، که به آن وتر (hypotenuse) می گویند. دو ضلع کوتاهتر اسامی خاص دیگری هم دارند، این اسامی بستگی به این دارد که با کدام زاویۀ حاده از این مثلث در زمان خاصی مشغول کار می باشید.
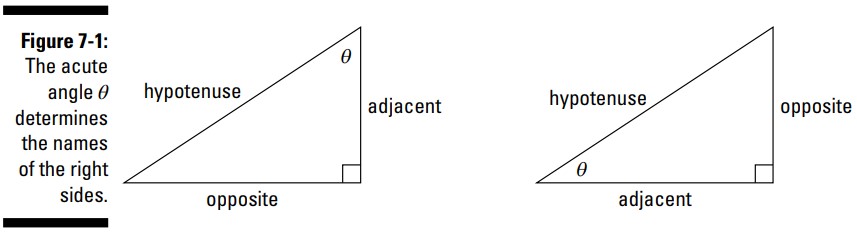
در ارتباط با زاویۀ \(\theta\) (شکل 1-7 را ببینید)، ساقی که در سمت دیگر \(\theta\) در این مثلث قرار دارد، ضلع روبرو (opposite side) نامیده می شود. این ضلع روبرو هرگز در امتداد یکی از نیمخطهایی که این زاویه را می سازند، قرار ندارد. ساق دیگر در این مثلث قائم الزاویه، ضلع مجاور (adjacent side) نامیده می شود. ضلع مجاور به معنای ضلع کناری می باشد، و در مورد مثلث های قائم الزاویه، ضلع مجاور کمک می کند تا همراه با وتر آن زاویۀ حاده را بسازید، زیرا در امتداد یکی از نیمخطهای این زاویه قرار دارد.
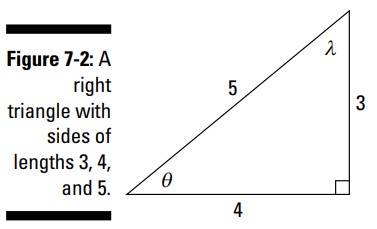
هر کدام از سه ضلع یک مثلث قائم الزاویه ـــ وتر، روبرو، و مجاور ـــ دارای یک طول یا اندازۀ مرتبط می باشد. و این سه طول یا اندازه شش نسبت متفاوت را می سازند. شکل 2-7 را بررسی کنید، که دارای اضلاعی با طول های \(3\)، \(4\)، و \(5\) می باشند.
شش نسبت متفاوتی که می توانید با اعداد \(3\)، \(4\)، و \(5\) بسازید عبارت از \(\frac{3}{4}\)، \(\frac{4}{5}\)، \(\frac{3}{5}\)، \(\frac{4}{3}\)، \(\frac{5}{4}\)، و \(\frac{5}{3}\) می باشند. این شش کسر تمام چیزی است که می توانید با استفاده از طول این سه ضلع ایجاد کنید. این نسبت ها خاص هستند، زیرا نشان دهندۀ تمامی مقادیر خروجیِ توابع مثلثاتی برای زوایای حاده در آن مثلث می باشند. و حتی بهتر از آن، شما می توانید مقدار یک زاویۀ مجهول را در یک مثلث قائم الزاویه صرفاً با ایجاد یکی از این نسبت ها و پیدا کردن اینکه کدام زاویه آن تابع مثلثاتی را دارد، محاسبه کنید.
هنگامی که از مثلث های قائم الزاویه برای تعریف توابع مثلثاتی استفاده می کنید، تابع مثلثاتی سینوس (sine)، که به اختصار به آن sin می گویند، دارای مقادیر ورودی که اندازۀ زوایا می باشد و مقادیر خروجی که از نسبت \(\frac{\text{opposite}}{\text{hypotenuse}}\) بدست می آیند، می باشد. شکل 2-7 دو زاویۀ حادۀ متفاوت را نشان می دهد، و هر کدام مقدار متفاوتی برای تابع سینوس دارد. این دو مقدار عبارت از \(\sin \theta = \frac{3}{5}\) و \(\sin \lambda = \frac{4}{5}\) .
حتی اگر هر دو ضلعی را که برای تابع سینوس مورد نیاز است، ندانید، در صورتیکه هر کدام از دو ضلع از سه ضلع یک مثلث را داشته باشید، می توانید سینوس را محاسبه کنید. به عنوان مثال، برای یافتن سینوس زاویۀ \(\alpha\) در یک مثلث قائم الزاویه که وتر آن برابر با \(10\) اینچ می باشد و ضلع مجاور آن برابر با \(8\) اینچ است، مراحل زیر را دنبال کنید:
تابع مثلثاتی کسینوس (cosine)، که به اختصار cos نامیده می شود، با تشکیل این نسبت کار می کند: \(\frac{\text{adjacent}}{\text{hypotenuse}}\) . دوباره شکل 2-7 را ببینید، و خواهید دید که کسینوس این دو زاویه برابر با \(\cos \theta=\frac{4}{5}\) و \(\cos \lambda = \frac{3}{5}\) می باشند. وضعیت این نسبت مشابه تابع سینوس می باشد ـــ مقادیر کوچکتر یا برابر با \(1\) می باشند (حالت دیگر تنها در صورتی رخ می دهد که مثلث شما یک پاره خط منفرد باشد یا اینکه مشغول کار با دایره ها باشید)، هرگز از \(1\) بزرگتر نخواهد شد، زیرا وتر در مخرج قرار دارد.
حالا یک مثال داریم. برای یافتن کسینوس زاویۀ \(\beta\) در یک مثلث قائم الزاویه اگر دو ساق آن هر کدام دارای طول \(\sqrt{6}\) فوت باشند، این مراحل را انجام دهید:
سومین تابع مثلثاتی، تانژانت (tangent)، به اختصار tan نامیده می شود. این تابع صرفاً از اندازۀ دو ساق استفاده می کند و به هیچ وجه از وتر استفاده نمی کند. تانژانت با این نسبت توصیف می شود: \(\frac{\text{opposite}}{\text{adjacent}}\) . هیچ محدودیت یا قاعده ای بر روی اندازه های مربوطه در این اضلاع وجود ندارد ـــ ضلع روبرو می تواند بزرگتر باشد، یا ضلع مجاور می تواند بزرگتر باشد. بنابراین، نسبت تانژانت اعدادی را تولید می کند که بسیار بزرگ، بسیار کوچک، و هر چیزی که بین آنها هست، می باشند. اگر به شکل 2-7 برگردید، خواهید دید که تانژانت ها عبارت از \(\tan \theta = \frac{3}{4}\) و \(\tan \lambda = \frac{4}{3}\) می باشند. و در صورتیکه از خودتان می پرسید که آیا این دو تانژانت زوایایِ حاده همیشه معکوس یکدیگرند، پاسخ بله است. اتحادهای مثلثاتی در فصل 11 این پدیده را توضیح می دهند.
مثال زیر به شما نشان می دهد چگونه مقادیر تانژانت هر کدام از زوایای حاده در یک مثلث قائم الزاویه که در آن وتر برابر با \(25\) اینچ و یکی از ساقها برابر با \(7\) اینچ می باشد را پیدا کنید.
گاهی اوقات شما مجبور می شوید یک تابع مثلثاتی را به لحاظ تابع دیگری حل کنید.
در مثال زیر، کسینوس زاویۀ \(\lambda\) برابر با \(\frac{12}{13}\) است. مقادیر سینوس و تانژانت \(\lambda\) چه می باشند؟
یک مثلث قائم الزاویه را در نظر بگیرید و یک ارتفاع (altitude) بر روی وترِ آن ترسیم کنید. چه چیزی بدست می آورید؟ شما مفتخر به دریافت سه مثلث قائم الزاویۀ مشابه هستید ـــ سه مثلث در اندازه های رو به کاهش، همگی دارای اندازۀ زوایای برابر. به عنوان مثالی از این وضعیت، نگاهی به شکل 4-7 بیندازید. زوایای حاده با \(\alpha\) و \(\beta\) نامگذاری شده اند تا برای یافتن ویژگی تشابه به شما کمک کنند.
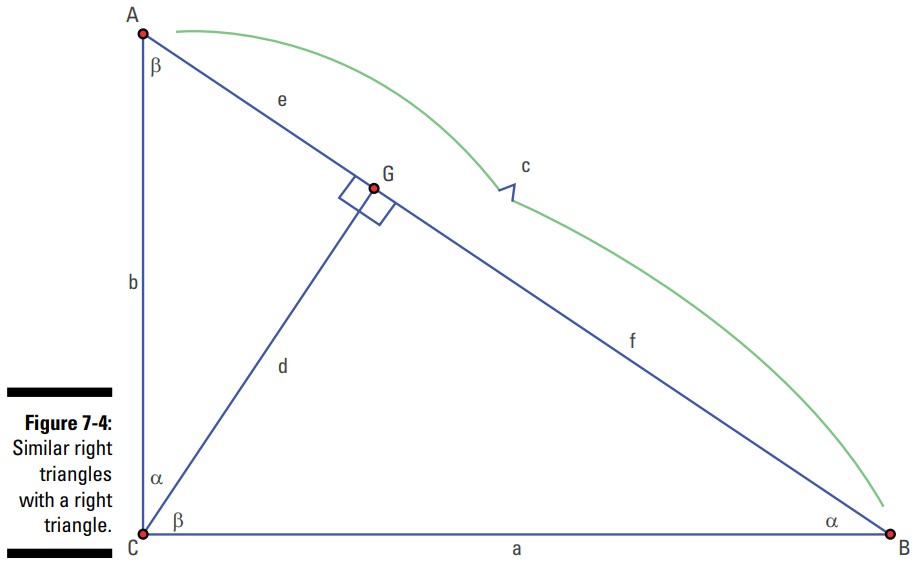
زوایای \(\alpha\) و \(\beta\) متمم می باشند و در هر کدام از این سه مثلث ظاهر شده اند. مثلث \(ABC\) با مثلث \(ACG\) مشابه می باشد، و هر دوی آنها با مثلث \(CBG\) مشابه هستند. من در دادن این اسامی با اولین حرف الفبا در رأس با زاویۀ \(\alpha\)، و دومین حرف الفبا در رأس با زاویۀ \(\beta\)، و آخرین حرف در زاویۀ قائمه، با دقت عمل کرده ام و مراقب بوده ام.
نامگذاری با دقت این مثلث ها شما را قادر می سازد تا توابع مثلثاتی این سه مثلث متفاوت را در معادلاتی که مقادیر آنها را مقایسه می کنند، بنویسید. به عنوان مثال، از آنجا که \(\triangle{ABC} \sim \triangle{ACG} \sim \triangle{CBG}\)، شما می توانید معادلاتی بنویسید که شامل نسبتهایی از اضلاع متناظر در این مثلث ها باشند. اگر نسبتهای ساق های بزرگتر را که بر ساقهای کوچکتر تقسیم شده اند، بنویسید، خواهید داشت:
$$\frac{a}{b} = \frac{d}{e} = \frac{f}{d}$$
حالا، نگاهی به تانژانت زاویۀ \(\beta\) در هر مثلث بیندازید. در \(\triangle{ABC}\)، \(\tan \beta =\frac{a}{b}\). در \(\triangle{ACG}\)، \(\tan \beta = \frac{d}{e}\). در \(\triangle{CBG}\)، \(\tan \beta=\frac{f}{d}\) .
اینها و ارتباطات دیگر شما را به چندین معادلۀ دیگر همچون قوانین وسطین تناسب (means) و طرفین تناسب (extremes) قادر می سازند:
و حالا به عنوان بخش جالب کار می پردازیم: افسانۀ یک سرآشپز هندی با نام SohCahToa (اینگونه بخوانید: سُکات آُ). سالها پیش، یک قبیله از آمریکایی های هندی تبار در امتداد رودخانۀ ایلینوی زندگی می کردند، که مشغول شکار، ماهیگیری و هر چیز ضروریِ دیگر برای زندگی در صلح و آرامش بودند. یک جوان شجاع سعی داشت تا استفاده از تیر و کمانش را به صورت موثر بیاموزد، و انواع مشکلات را در این مسیر داشت. دست آخر ناامید شد و به چیزی که تصور می کرد نرم باشد لگد محکمی زد، اما از شانس بدش یک صخرۀ سفت بود. انگشت پای او کبود و دردناک شد و شب و روز درد می کرد. او آن را پانسمان کرد، ماساژ داد، و سعی کرد دردش را نادیده بگیرد، اما هیچ چیزی او را به آرامش نرساند. مادر او که یک زن سرخپوست فهمیده بود، در نهایت از شکایت و غرولند او کلافه شد و فریاد زد: "همین الان به سمت رودخانه برو و سُ کا تُ آ (Soh Cah Toa)!" . جوان شجاع به سمت رودخانه رفت، پایش را در آب سرد رودخانه فرو برد، و تسکین یافت. او هرگز در کار با تیر و کمان حرفه ای نشد، و به لگد زدن به چیزها در ناامیدی ادامه داد. خیلی زود، او به SohCahToa مشهور شد.
مسلماً این داستان خیلی بی مزه و خسته کننده بود، اما هرگاه که بخواهید نسبت بین سه تابع مثلثاتی پایه ای را بیابید برایتان بسیار مفید خواهد بود:
افرادیکه مثلثات را در گذشته مطالعه کرده باشند، ممکن نیست چیز زیادی از آن را به خاطر داشته باشند، اما یک چیز که قطعاً به یادشان مانده است SohCahToa می باشد، البته اگر این داستان، یا چیزی مشابه آن را شنیده باشند.

این شش تابع مثلثاتی یک چیز را از شما تقاضا می کنند ـــ وارد کردن اندازۀ یک زاویه ـــ و سپس عددی را به عنوان خروجی به شما می دهند. این خروجی ها می توانند هر عدد حقیقی، از بی نهایت کوچک تا بی نهایت بزرگ و هر چیز دیگری بین آنها، باشند. نتایجی که دریافت می کنید بستگی به تابع مثلثاتی مورد استفاده دارد. اگرچه برخی از محاسبات اولیه نسبتاً خسته کننده بودند، امروزه ماشین حسابهای دستی همه چیز را بسیار ساده تر کرده اند.
توابع مثلثاتی چگونه کار می کنند؟ آشنایی با واژۀ SohCahToa
SohCahToa کیست یا چیست؟ شاید یک نوع پاستای ایتالیایی، شاید یک پرنسس بومی آمریکایی، یا شاید دارویی معجزه آور باشد؟ در واقع هیچکدام از اینها نیست. بعضی از معلم های ریاضی باهوش این واژه را اختراع کرده اند تا در یادآوری نسبت های مثلثاتی به دانش آموزان کمک کند. بعد از آن بود که این کلمه در همه جا پخش شد. قبل از اینکه به شما توضیح بدهم SohCahToa چیست، باید بدانید که این حروف مخفف چه چیزهایی هستند. حروف بزرگ \(S\)، \(C\)، و \(T\) به ترتیب مخفف توابع مثلثاتی sine (سینوس)، cosine (کسینوس)، و tangent (تانژانت) می باشند. حروف کوچک نسبتهای آنها را در یک مثلث قائم الزاویه نشان می دهند.
یادداشت مترجم: SohCahToa یک کلمۀ معنادار انگلیسی نمی باشد و در واقع مخفف نویسی است، آن را به صورت "سُکاتُ آ" یا "سُ کا تُ آ" تلفظ می کنند.
سه ضلع یک مثلث قائم الزاویه
یک مثلث قائم الزاویه دو ضلع کوتاهتر، یا دو ساق، دارد و بلندترین ضلع، مقابل زاویۀ قائمه است، که به آن وتر (hypotenuse) می گویند. دو ضلع کوتاهتر اسامی خاص دیگری هم دارند، این اسامی بستگی به این دارد که با کدام زاویۀ حاده از این مثلث در زمان خاصی مشغول کار می باشید.
در ارتباط با زاویۀ \(\theta\) (شکل 1-7 را ببینید)، ساقی که در سمت دیگر \(\theta\) در این مثلث قرار دارد، ضلع روبرو (opposite side) نامیده می شود. این ضلع روبرو هرگز در امتداد یکی از نیمخطهایی که این زاویه را می سازند، قرار ندارد. ساق دیگر در این مثلث قائم الزاویه، ضلع مجاور (adjacent side) نامیده می شود. ضلع مجاور به معنای ضلع کناری می باشد، و در مورد مثلث های قائم الزاویه، ضلع مجاور کمک می کند تا همراه با وتر آن زاویۀ حاده را بسازید، زیرا در امتداد یکی از نیمخطهای این زاویه قرار دارد.

شش نسبت: مرتبط با این سه ضلع
هر کدام از سه ضلع یک مثلث قائم الزاویه ـــ وتر، روبرو، و مجاور ـــ دارای یک طول یا اندازۀ مرتبط می باشد. و این سه طول یا اندازه شش نسبت متفاوت را می سازند. شکل 2-7 را بررسی کنید، که دارای اضلاعی با طول های \(3\)، \(4\)، و \(5\) می باشند.

شش نسبت متفاوتی که می توانید با اعداد \(3\)، \(4\)، و \(5\) بسازید عبارت از \(\frac{3}{4}\)، \(\frac{4}{5}\)، \(\frac{3}{5}\)، \(\frac{4}{3}\)، \(\frac{5}{4}\)، و \(\frac{5}{3}\) می باشند. این شش کسر تمام چیزی است که می توانید با استفاده از طول این سه ضلع ایجاد کنید. این نسبت ها خاص هستند، زیرا نشان دهندۀ تمامی مقادیر خروجیِ توابع مثلثاتی برای زوایای حاده در آن مثلث می باشند. و حتی بهتر از آن، شما می توانید مقدار یک زاویۀ مجهول را در یک مثلث قائم الزاویه صرفاً با ایجاد یکی از این نسبت ها و پیدا کردن اینکه کدام زاویه آن تابع مثلثاتی را دارد، محاسبه کنید.
تابع سینوس: ضلع روبرو بر روی وتر
هنگامی که از مثلث های قائم الزاویه برای تعریف توابع مثلثاتی استفاده می کنید، تابع مثلثاتی سینوس (sine)، که به اختصار به آن sin می گویند، دارای مقادیر ورودی که اندازۀ زوایا می باشد و مقادیر خروجی که از نسبت \(\frac{\text{opposite}}{\text{hypotenuse}}\) بدست می آیند، می باشد. شکل 2-7 دو زاویۀ حادۀ متفاوت را نشان می دهد، و هر کدام مقدار متفاوتی برای تابع سینوس دارد. این دو مقدار عبارت از \(\sin \theta = \frac{3}{5}\) و \(\sin \lambda = \frac{4}{5}\) .
سینوس همیشه اندازۀ ضلع روبرو (opposite side) تقسیم بر اندازۀ وتر (hypotenuse) می باشد. از آنجا که وتر همیشه بلندترین ضلع می باشد، عدد موجود در مخرج این نسبت همواره از عدد موجود در صورت آن بزرگتر است. به همین دلیل، خروجی تابع سینوس همیشه یک کسر واقعی (proper fraction) می باشد ـــ هرگز عددی برابر یا بزرگتر از \(1\) نخواهد بود، مگر اینکه طول ضلع روبرو با وتر برابر باشد (که تنها در صورتی رخ می دهد که مثلث شما یک پاره خط منفرد باشد یا شما مشغول کار با دایره ها باشید ـــ فصل 8 را ببینید).
حتی اگر هر دو ضلعی را که برای تابع سینوس مورد نیاز است، ندانید، در صورتیکه هر کدام از دو ضلع از سه ضلع یک مثلث را داشته باشید، می توانید سینوس را محاسبه کنید. به عنوان مثال، برای یافتن سینوس زاویۀ \(\alpha\) در یک مثلث قائم الزاویه که وتر آن برابر با \(10\) اینچ می باشد و ضلع مجاور آن برابر با \(8\) اینچ است، مراحل زیر را دنبال کنید:
-
طول ضلع روبروی \(\alpha\) را بیابید.
با استفاده از قضیۀ فیثاغورث، \(a^2+b^2=c^2\)، \(a\) را برابر با \(8\) و \(c\) را برابر با \(10\) قرار دهید. هنگامی که اعداد را در این قضیه جایگذاری کنید و آن را برای بدست آوردن \(b\) حل کنید، به این نتایج می رسید:
$$
8^2+b^2=10^2 \\
64 + b^2=100 \\
b^2=36 \\
b=6
$$
پس، ضلع روبرو برابر با \(6\) اینچ می باشد.
-
از نسبت سینوس، ضلع روبرو بر روی وتر، استفاده کنید.
$$\sin \alpha = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{6}{10}=\frac{3}{5}$$
تابع کسینوس: ضلع مجاور بر روی وتر
تابع مثلثاتی کسینوس (cosine)، که به اختصار cos نامیده می شود، با تشکیل این نسبت کار می کند: \(\frac{\text{adjacent}}{\text{hypotenuse}}\) . دوباره شکل 2-7 را ببینید، و خواهید دید که کسینوس این دو زاویه برابر با \(\cos \theta=\frac{4}{5}\) و \(\cos \lambda = \frac{3}{5}\) می باشند. وضعیت این نسبت مشابه تابع سینوس می باشد ـــ مقادیر کوچکتر یا برابر با \(1\) می باشند (حالت دیگر تنها در صورتی رخ می دهد که مثلث شما یک پاره خط منفرد باشد یا اینکه مشغول کار با دایره ها باشید)، هرگز از \(1\) بزرگتر نخواهد شد، زیرا وتر در مخرج قرار دارد.
این دو نسبت مربوط به کسینوس با نسبتهای مربوط به سینوس یکسان می باشند ـــ با این تفاوت که زوایا معکوس شده اند. این ویژگی برای سینوس ها و کسینوس های زوایای متمم (complementary angles) در یک مثلث قائم الزاویه صدق می کند (بدین معنا که زوایایی که مجموع آنها \(90\) درجه می شود).
اگر \(\theta\) و \(\lambda\) دو زاویۀ حاده از یک مثلث قائم الزاویه باشند، آن گاه \(\sin \theta = \cos \lambda\) و \(\cos \theta = \sin \lambda\) .
حالا یک مثال داریم. برای یافتن کسینوس زاویۀ \(\beta\) در یک مثلث قائم الزاویه اگر دو ساق آن هر کدام دارای طول \(\sqrt{6}\) فوت باشند، این مراحل را انجام دهید:
-
طول وتر را بیابید.
با استفاده از قضیۀ فیثاغورث، \(a^2+b^2=c^2\)، و جایگزینی \(a\) و \(b\) با اندازۀ داده شده، این معادله را برای بدست آوردن \(c\) حل کنید.
$$
\bigl( \sqrt{6} \bigr)^2 + \bigl( \sqrt{6} \bigr)^2 = c^2 \\
6+6=c^2 \\
12=c^2 \\
\sqrt{12}=c \\
2\sqrt{3}=c
$$
طول وتر برابر است با \(2\sqrt{3}\) فوت.
-
از نسبت مربوط به کسینوس، ضلع مجاور بر روی وتر، استفاده کنید تا پاسخ را بیابید.
$$\cos \beta = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{\sqrt{6}}{2\sqrt{3}}=\frac{\sqrt{2}}{2}$$
تابع تانژانت: ضلع روبرو بر روی ضلع مجاور
سومین تابع مثلثاتی، تانژانت (tangent)، به اختصار tan نامیده می شود. این تابع صرفاً از اندازۀ دو ساق استفاده می کند و به هیچ وجه از وتر استفاده نمی کند. تانژانت با این نسبت توصیف می شود: \(\frac{\text{opposite}}{\text{adjacent}}\) . هیچ محدودیت یا قاعده ای بر روی اندازه های مربوطه در این اضلاع وجود ندارد ـــ ضلع روبرو می تواند بزرگتر باشد، یا ضلع مجاور می تواند بزرگتر باشد. بنابراین، نسبت تانژانت اعدادی را تولید می کند که بسیار بزرگ، بسیار کوچک، و هر چیزی که بین آنها هست، می باشند. اگر به شکل 2-7 برگردید، خواهید دید که تانژانت ها عبارت از \(\tan \theta = \frac{3}{4}\) و \(\tan \lambda = \frac{4}{3}\) می باشند. و در صورتیکه از خودتان می پرسید که آیا این دو تانژانت زوایایِ حاده همیشه معکوس یکدیگرند، پاسخ بله است. اتحادهای مثلثاتی در فصل 11 این پدیده را توضیح می دهند.
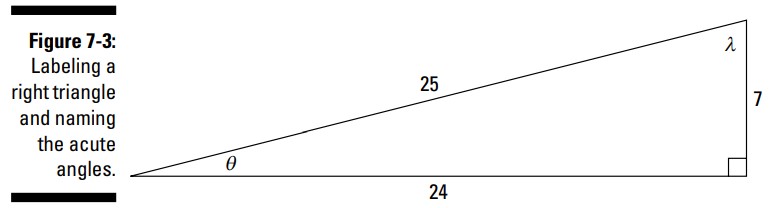
مثال زیر به شما نشان می دهد چگونه مقادیر تانژانت هر کدام از زوایای حاده در یک مثلث قائم الزاویه که در آن وتر برابر با \(25\) اینچ و یکی از ساقها برابر با \(7\) اینچ می باشد را پیدا کنید.
-
طول ضلع مجهول را بیابید.
با استفاده از قضیۀ فیثاغورث، \(a^2+b^2=c^2\)، و قرار دادن \(7\) در \(a\) و \(25\) در \(c\)، و حل کردن آن برای ضلع مجهول، \(b\)، در می یابید که طول این ضلع مجهول برابر با \(24\) اینچ می باشد:
$$
7^2+b^2=25^2 \\
b^2 = 25^2 - 7^2 \\
= 625-49 \\
= 576 \\
b=24
$$
-
برای این زوایای حاده اسم انتخاب کنید تا بتوانید ضلع روبرو و ضلع مجاور را تعیین کنید.
ساده ترین روش برای انجام این کار ترسیم یک تصویر و برچسب گذاری آن می باشد ـــ نگاهی به شکل 3-7 بیندازید.
این دو زاویۀ حاده با حروف یونانیِ \(\theta\) و \(\lambda\) نامگذاری شده اند. ضلع روبروی \(\theta\) دارای اندازۀ \(7\) اینچ، و ضلع مجاور آن دارای اندازۀ \(24\) اینچ می باشد. در مورد زاویۀ \(\lambda\)، ضلع روبرو \(24\) اینچ، و ضلع مجاور \(7\) اینچ می باشد.
-
این دو نسبت تانژانت را با استفاده از مقادیر \(7\)، \(24\)، و \(25\) تشکیل دهید.
$$\tan \theta = \frac{\text{opposite}}{\text{adjacent}} = \frac{7}{24} \\
\tan \lambda = \frac{opposite}{adjacent} = \frac{24}{7}$$

استفاده از یک تابع برای بدست آوردن دیگری
گاهی اوقات شما مجبور می شوید یک تابع مثلثاتی را به لحاظ تابع دیگری حل کنید.
در مثال زیر، کسینوس زاویۀ \(\lambda\) برابر با \(\frac{12}{13}\) است. مقادیر سینوس و تانژانت \(\lambda\) چه می باشند؟
-
اضلاع داده شده توسط تابع کسینوس را شناسایی کنید.
نسبت کسینوس برابر با \(\frac{\text{adjacent}}{\text{hypotenuse}}\) می باشد. با استفاده از این نسبت داده شده، اندازۀ ضلع مجاور برابر با \(12\) واحد، و وتر برابر با \(13\) واحد می باشد.
-
اندازۀ ضلع مجهول را بیابید.
با استفاده از قضیۀ فیثاغورث، شما در می یابید که ضلع مجهول (ضلع روبرو) برابر با \(5\) واحد است.
$$
12^2+b^2=13^2 \\
b^2 = 13^2 - 12^2 \\
= 169-144 \\
=25\\
b=5
$$
-
مقادیر سینوس و تانژانت را تعیین کنید.
سینوس برابر با \(\frac{\text{opposite}}{\text{hypotenuse}}\) و تانژانت برابر با \(\frac{\text{opposite}}{\text{adjacent}}\) است، پس \(\sin \lambda = \frac{5}{13}\) و \(\tan \lambda = \frac{5}{12}\) می باشند.
مثلث های قائم الزاویۀ مشابه درون یک مثلث قائم الزاویه
یک مثلث قائم الزاویه را در نظر بگیرید و یک ارتفاع (altitude) بر روی وترِ آن ترسیم کنید. چه چیزی بدست می آورید؟ شما مفتخر به دریافت سه مثلث قائم الزاویۀ مشابه هستید ـــ سه مثلث در اندازه های رو به کاهش، همگی دارای اندازۀ زوایای برابر. به عنوان مثالی از این وضعیت، نگاهی به شکل 4-7 بیندازید. زوایای حاده با \(\alpha\) و \(\beta\) نامگذاری شده اند تا برای یافتن ویژگی تشابه به شما کمک کنند.

زوایای \(\alpha\) و \(\beta\) متمم می باشند و در هر کدام از این سه مثلث ظاهر شده اند. مثلث \(ABC\) با مثلث \(ACG\) مشابه می باشد، و هر دوی آنها با مثلث \(CBG\) مشابه هستند. من در دادن این اسامی با اولین حرف الفبا در رأس با زاویۀ \(\alpha\)، و دومین حرف الفبا در رأس با زاویۀ \(\beta\)، و آخرین حرف در زاویۀ قائمه، با دقت عمل کرده ام و مراقب بوده ام.
نامگذاری با دقت این مثلث ها شما را قادر می سازد تا توابع مثلثاتی این سه مثلث متفاوت را در معادلاتی که مقادیر آنها را مقایسه می کنند، بنویسید. به عنوان مثال، از آنجا که \(\triangle{ABC} \sim \triangle{ACG} \sim \triangle{CBG}\)، شما می توانید معادلاتی بنویسید که شامل نسبتهایی از اضلاع متناظر در این مثلث ها باشند. اگر نسبتهای ساق های بزرگتر را که بر ساقهای کوچکتر تقسیم شده اند، بنویسید، خواهید داشت:
$$\frac{a}{b} = \frac{d}{e} = \frac{f}{d}$$
حالا، نگاهی به تانژانت زاویۀ \(\beta\) در هر مثلث بیندازید. در \(\triangle{ABC}\)، \(\tan \beta =\frac{a}{b}\). در \(\triangle{ACG}\)، \(\tan \beta = \frac{d}{e}\). در \(\triangle{CBG}\)، \(\tan \beta=\frac{f}{d}\) .
اینها و ارتباطات دیگر شما را به چندین معادلۀ دیگر همچون قوانین وسطین تناسب (means) و طرفین تناسب (extremes) قادر می سازند:
-
\(d^2=e \cdot f\): مربع ارتفاع برابر است با حاصلضرب دو بخش وتر.
-
\(b^2=e \cdot c\): مربع یک ساق برابر است با حاصلضرب بخشی از وتر که مجاور آن ساق می باشد در وتر.
ذخیره کردن این قوانین در یک جای امن: افسانۀ SohCahToa
و حالا به عنوان بخش جالب کار می پردازیم: افسانۀ یک سرآشپز هندی با نام SohCahToa (اینگونه بخوانید: سُکات آُ). سالها پیش، یک قبیله از آمریکایی های هندی تبار در امتداد رودخانۀ ایلینوی زندگی می کردند، که مشغول شکار، ماهیگیری و هر چیز ضروریِ دیگر برای زندگی در صلح و آرامش بودند. یک جوان شجاع سعی داشت تا استفاده از تیر و کمانش را به صورت موثر بیاموزد، و انواع مشکلات را در این مسیر داشت. دست آخر ناامید شد و به چیزی که تصور می کرد نرم باشد لگد محکمی زد، اما از شانس بدش یک صخرۀ سفت بود. انگشت پای او کبود و دردناک شد و شب و روز درد می کرد. او آن را پانسمان کرد، ماساژ داد، و سعی کرد دردش را نادیده بگیرد، اما هیچ چیزی او را به آرامش نرساند. مادر او که یک زن سرخپوست فهمیده بود، در نهایت از شکایت و غرولند او کلافه شد و فریاد زد: "همین الان به سمت رودخانه برو و سُ کا تُ آ (Soh Cah Toa)!" . جوان شجاع به سمت رودخانه رفت، پایش را در آب سرد رودخانه فرو برد، و تسکین یافت. او هرگز در کار با تیر و کمان حرفه ای نشد، و به لگد زدن به چیزها در ناامیدی ادامه داد. خیلی زود، او به SohCahToa مشهور شد.
مسلماً این داستان خیلی بی مزه و خسته کننده بود، اما هرگاه که بخواهید نسبت بین سه تابع مثلثاتی پایه ای را بیابید برایتان بسیار مفید خواهد بود:
-
Soh: مخفف Sine Opposite Hypotenuse به معنی سینوس روبرو وتر، می باشد.
-
Cah: مخفف Cosine Adjacent Hypotenuse به معنای کسینوس مجاور وتر می باشد.
-
Toa: مخفف Tangent Opposite Adjacent به معنای تانژانت روبرو مجاور می باشد.
افرادیکه مثلثات را در گذشته مطالعه کرده باشند، ممکن نیست چیز زیادی از آن را به خاطر داشته باشند، اما یک چیز که قطعاً به یادشان مانده است SohCahToa می باشد، البته اگر این داستان، یا چیزی مشابه آن را شنیده باشند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: