خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
رایج ترین زوایا در هندسه

شما ممکن است یک برنامۀ تلویزیونی، دسر، یا رنگ محبوب داشته باشید. با این حال، معمولاً داشتن یک زاویۀ محبوب در لیست علاقمندیهای اشخاص قرار ندارد. اما داشتن یک زاویۀ محبوب واقعاً زیاده روی نیست. زاویۀ محبوب من، زاویۀ \(30\) درجه می باشد.

رایج ترین زوایا آنهایی هستند که اندازۀ آنها مضربی از \(15\) می باشد. در بالای این لیست زوایای \(30\)، \(60\)، و \(90\) درجه قرار دارند. زاویۀ محبوب دیگر \(45\) درجه می باشد. دلیل محبوبیت این زوایا اینست که همگی آنها \(360\) درجه را به صورت برابر تقسیم می کنند. این تقسیم های دقیق منجر به مقادیر زیباتر از حد معمول برای توابع مثلثاتی مختلف می گردند.
یک روش برای اینکه زوایایی حتی بیش از این چهار زاویه را به کار گیرید ـــ \(30\)، \(45\)، \(60\)، و \(90\) ـــ اینست که به مضرب های آنها که تا \(360\) پیش می روند بنگرید. توابع مثلثاتی برای این چهار زاویۀ پایه ای اول و توابع مثلثاتیِ مضرب های آنها به یکدیگر مرتبط می باشند (فصل 8 را ببینید). لیست همیشه محبوب ها شامل مضربهایی از \(30\) درجه می باشند (\(30\)، \(60\)، \(90\)، \(120\)، \(150\)، \(180\)، \(210\)، \(240\)، \(270\)، \(300\)، و \(330\)) و برخی از مضربهای \(15\) درجه که بین آنها هستند می باشند: \(45\)، \(135\)، \(225\)، و \(315\). تمامی این مضربها چهار ربع صفحه را در اولین بار جدا می کنند. همچنین یک زاویۀ \(0\) درجه به شدت محبوب است. یک اندازۀ \(0\) درجه به لحاظ فنی مضربی از تمامی این اندازه ها می باشد، و شما به این دلیل که نقطۀ آغاز می باشد به آن نیاز دارید.
با وجود اینکه یک ماشین حساب علمی مقادیر توابع مثلثاتی هر زاویه ای، و نه صرفاً زوایای محبوب شما، را به شما می دهد، مقادیری که برای بیشتر آن زوایا به شما نشان می دهد صرفاً تخمینی هستند. به عنوان مثال، مقدار دقیق سینوس \(60\) درجه برابر با \(\frac{\sqrt{3}}{2}\) می باشد. با این حال، از آنجا که رادیکال اعدادی که مربع کامل نیستند، غیرگویا می باشند و دارای بی نهایت مقدار اعشاری می باشند، یک ماشین حساب آن عدد را تا تعداد معینی ارقام اعشاری نگه می دارد و بقیه اش را گرد می کند. در این مورد، \(\frac{\sqrt{3}}{2} \approx 0.8660254038\) . این عدد اعشاری تعداد ارقام اعشاری خیلی بیش از آنچه شما نیاز دارید را در خودش دارد ـــ به طور معمول، سه یا چهار رقم اعشار کفایت می کند.
فرآیند ایجاد یک جدول از مقادیر توابع مثلثاتی، که در این بخش توضیح خواهم داد، برای یادآوری ساده می باشد، بنابراین شما می توانید هرجا که نیاز باشد یکی از آنها را به سرعت بسازید ـــ خواه بر روی کاغذ و خواه در حافظه تان.
زوایایی که بیشتر اوقات در مثلثات مورد استفاده قرار می گیرند، دارای توابع مثلثاتی با مقادیر دقیق راحت می باشند. سایر زوایا به زیبایی این زوایای رایج همکاری نمی کنند.
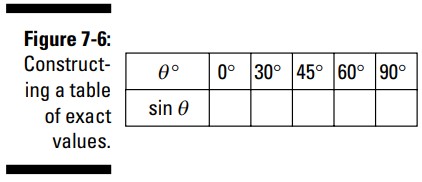
یک روش سریع و ساده برای حفظ کردن مقادیر دقیق توابع مثلثاتیِ زوایای رایج اینست که یک جدول بسازیم، با تابع سینوس و با الگویی از کسرها و رادیکال ها، آغاز کنیم. جدولی که در ردیف بالایی آن زوایا قرار گرفته اند، مشابه شکل 6-7 بسازید. اولین تابع در ردیف بعدی، سینوس (sine) می باشد.
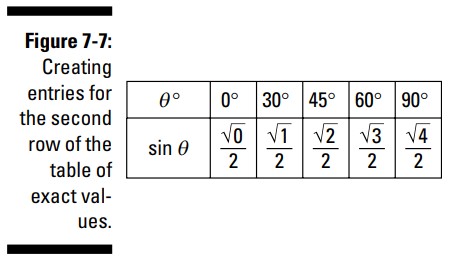
مقادیر \(\sin \theta\) در ردیف دوم، کسرها و رادیکال هایی با الگوهای زیر می باشند:
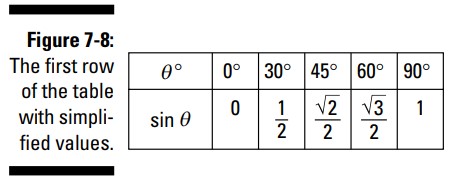
در ادامه، کسرهایی که امکان ساده شدن دارند را ساده کنید، جدول به چیزی که در شکل 8-7 می بینید، تبدیل می گردد:
$$\frac{\sqrt{0}}{2}=0, \frac{\sqrt{1}}{2}=\frac{1}{2}, \frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2},\frac{\sqrt{4}}{2}=1$$
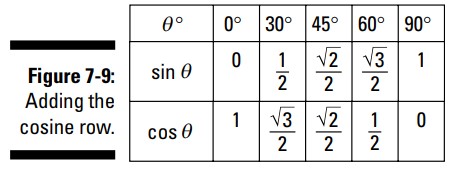
ردیف بعدی، برای کسینوس، همانطور که شکل 9-7 نشان می دهد، صرفاً همان ردیف سینوس است که ترتیبش برعکس شده است. دلیل این رخداد اینست که شما زوایایی دارید که در ترتیب معکوس، متمم یکدیگر می باشند.
ردیف بعدی مربوط به تانژانت است. در یک مثلث قائم الزاویه، تانژانت یک زاویۀ حاده را با نسبت \(\frac{\text{opposite}}{\text{adjacent}}\) بدست می آورید. هنگامی که سینوس را بر روی کسینوس تقسیم کنید، به همان نسبت می رسید. در اینجا چگونگی این کار را می بینید:
$$
\require{cancel}
\frac{\text{sine}}{\text{cosine}} = \frac{\frac{\text{opposite}}{\text{hypotenuse}}}{\frac{\text{adjacent}}{\text{hypotenuse}}} = \frac{\text{opposite}}{\cancel{\text{hypotenuse}}} \cdot \frac{\cancel{\text{hypotenuse}}}{\text{adjacent}} =\frac{\text{opposite}}{\text{adjacent}}
$$
از آنجا که در حال حاضر شما مقادیر سینوس و کسینوس را می دانید، می توانید از این ویژگی (تانژانت برابر است با سینوس تقسیم بر کسینوس) استفاده کنید تا مقادیر تانژانت در جدول را بدست آورید:
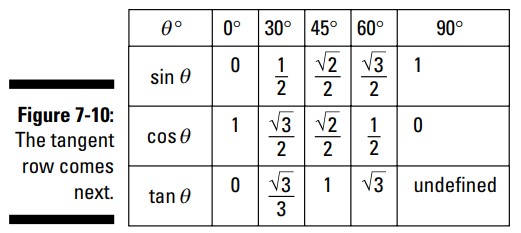
شکل 10-7 را که در آن ردیف تانژانت نیز در جدول تکمیل شده است، ببینید.
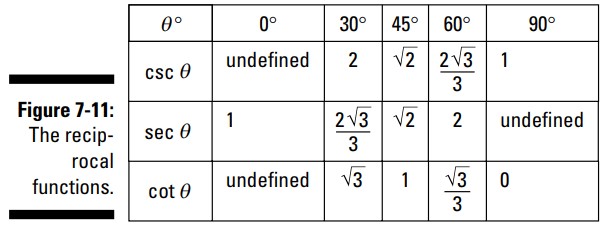
پیشتر در همین فصل دانستید که توابع مثلثاتی معکوس، مقادیرشان معکوس توابع اصلی مربوطه می باشد. معکوس سینوس برابر با کسکانت است، بنابراین هر مقدار در تابع کسکانت معکوس سینوس می باشد. رویۀ یکسانی در مورد دو تابع معکوس دیگر جریان دارد. جدول 11-7 معکوس ها را در هر مورد، در شکل ساده شده، نشان می دهد. هرجا که واژۀ undefined (تعریف نشده) را می بینید، به این دلیل است که تابع اصلی دارای مقدار \(0\) است و معکوس \(0\) مقداری ندارد.

شناسایی رایج ترین زوایا
رایج ترین زوایا آنهایی هستند که اندازۀ آنها مضربی از \(15\) می باشد. در بالای این لیست زوایای \(30\)، \(60\)، و \(90\) درجه قرار دارند. زاویۀ محبوب دیگر \(45\) درجه می باشد. دلیل محبوبیت این زوایا اینست که همگی آنها \(360\) درجه را به صورت برابر تقسیم می کنند. این تقسیم های دقیق منجر به مقادیر زیباتر از حد معمول برای توابع مثلثاتی مختلف می گردند.
یک روش برای اینکه زوایایی حتی بیش از این چهار زاویه را به کار گیرید ـــ \(30\)، \(45\)، \(60\)، و \(90\) ـــ اینست که به مضرب های آنها که تا \(360\) پیش می روند بنگرید. توابع مثلثاتی برای این چهار زاویۀ پایه ای اول و توابع مثلثاتیِ مضرب های آنها به یکدیگر مرتبط می باشند (فصل 8 را ببینید). لیست همیشه محبوب ها شامل مضربهایی از \(30\) درجه می باشند (\(30\)، \(60\)، \(90\)، \(120\)، \(150\)، \(180\)، \(210\)، \(240\)، \(270\)، \(300\)، و \(330\)) و برخی از مضربهای \(15\) درجه که بین آنها هستند می باشند: \(45\)، \(135\)، \(225\)، و \(315\). تمامی این مضربها چهار ربع صفحه را در اولین بار جدا می کنند. همچنین یک زاویۀ \(0\) درجه به شدت محبوب است. یک اندازۀ \(0\) درجه به لحاظ فنی مضربی از تمامی این اندازه ها می باشد، و شما به این دلیل که نقطۀ آغاز می باشد به آن نیاز دارید.
تعیین مقدار دقیق توابع
با وجود اینکه یک ماشین حساب علمی مقادیر توابع مثلثاتی هر زاویه ای، و نه صرفاً زوایای محبوب شما، را به شما می دهد، مقادیری که برای بیشتر آن زوایا به شما نشان می دهد صرفاً تخمینی هستند. به عنوان مثال، مقدار دقیق سینوس \(60\) درجه برابر با \(\frac{\sqrt{3}}{2}\) می باشد. با این حال، از آنجا که رادیکال اعدادی که مربع کامل نیستند، غیرگویا می باشند و دارای بی نهایت مقدار اعشاری می باشند، یک ماشین حساب آن عدد را تا تعداد معینی ارقام اعشاری نگه می دارد و بقیه اش را گرد می کند. در این مورد، \(\frac{\sqrt{3}}{2} \approx 0.8660254038\) . این عدد اعشاری تعداد ارقام اعشاری خیلی بیش از آنچه شما نیاز دارید را در خودش دارد ـــ به طور معمول، سه یا چهار رقم اعشار کفایت می کند.
در مثلثات، شما به وفور از مقدار دقیق بیشتر زوایای محبوب استفاده می کنید، زیرا آنها نتایج بهتری در محاسبات و کاربردها می دهند، بنابراین حفظ کردن آن مقادیر دقیق ایدۀ خوبی است.
فرآیند ایجاد یک جدول از مقادیر توابع مثلثاتی، که در این بخش توضیح خواهم داد، برای یادآوری ساده می باشد، بنابراین شما می توانید هرجا که نیاز باشد یکی از آنها را به سرعت بسازید ـــ خواه بر روی کاغذ و خواه در حافظه تان.
یک جدول سریع برای سه تابع مثلثاتی اصلی
زوایایی که بیشتر اوقات در مثلثات مورد استفاده قرار می گیرند، دارای توابع مثلثاتی با مقادیر دقیق راحت می باشند. سایر زوایا به زیبایی این زوایای رایج همکاری نمی کنند.
یک روش سریع و ساده برای حفظ کردن مقادیر دقیق توابع مثلثاتیِ زوایای رایج اینست که یک جدول بسازیم، با تابع سینوس و با الگویی از کسرها و رادیکال ها، آغاز کنیم. جدولی که در ردیف بالایی آن زوایا قرار گرفته اند، مشابه شکل 6-7 بسازید. اولین تابع در ردیف بعدی، سینوس (sine) می باشد.

مقادیر \(\sin \theta\) در ردیف دوم، کسرها و رادیکال هایی با الگوهای زیر می باشند:
-
هر کسر مخرجی از \(2\) دارد.
-
صورت این کسرها مقادیر رادیکالی با \(0\)، \(1\)، \(2\)، \(3\)، و \(4\) در زیر رادیکال، به ترتیبی که در شکل 7-7 می بینید، می باشند.

در ادامه، کسرهایی که امکان ساده شدن دارند را ساده کنید، جدول به چیزی که در شکل 8-7 می بینید، تبدیل می گردد:
$$\frac{\sqrt{0}}{2}=0, \frac{\sqrt{1}}{2}=\frac{1}{2}, \frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2},\frac{\sqrt{4}}{2}=1$$

ردیف بعدی، برای کسینوس، همانطور که شکل 9-7 نشان می دهد، صرفاً همان ردیف سینوس است که ترتیبش برعکس شده است. دلیل این رخداد اینست که شما زوایایی دارید که در ترتیب معکوس، متمم یکدیگر می باشند.

ردیف بعدی مربوط به تانژانت است. در یک مثلث قائم الزاویه، تانژانت یک زاویۀ حاده را با نسبت \(\frac{\text{opposite}}{\text{adjacent}}\) بدست می آورید. هنگامی که سینوس را بر روی کسینوس تقسیم کنید، به همان نسبت می رسید. در اینجا چگونگی این کار را می بینید:
$$
\require{cancel}
\frac{\text{sine}}{\text{cosine}} = \frac{\frac{\text{opposite}}{\text{hypotenuse}}}{\frac{\text{adjacent}}{\text{hypotenuse}}} = \frac{\text{opposite}}{\cancel{\text{hypotenuse}}} \cdot \frac{\cancel{\text{hypotenuse}}}{\text{adjacent}} =\frac{\text{opposite}}{\text{adjacent}}
$$
از آنجا که در حال حاضر شما مقادیر سینوس و کسینوس را می دانید، می توانید از این ویژگی (تانژانت برابر است با سینوس تقسیم بر کسینوس) استفاده کنید تا مقادیر تانژانت در جدول را بدست آورید:
-
تانژانت \(0\) درجه:
$$ \frac{0}{1}=0 $$
-
تانژانت \(30\) درجه:
$$\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{2} \cdot \frac{2}{\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$$
-
تانژانت \(45\) درجه:
$$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=1$$
-
تانژانت \(60\) درجه:
$$\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\frac{\sqrt{3}}{2} \cdot \frac{2}{1}=\frac{\sqrt{3}}{1}=\sqrt{3}$$
-
تانژانت \(90\) درجه برابر با \(\frac{1}{0}\) است، که تعریف نشده (undefined) می باشد. بنابراین، تانژانت \(90\) درجه مقداری نخواهد داشت ـــ به سادگی وجود ندارد.
شکل 10-7 را که در آن ردیف تانژانت نیز در جدول تکمیل شده است، ببینید.

یک جدول سریع برای سه تابع مثلثاتی معکوس
پیشتر در همین فصل دانستید که توابع مثلثاتی معکوس، مقادیرشان معکوس توابع اصلی مربوطه می باشد. معکوس سینوس برابر با کسکانت است، بنابراین هر مقدار در تابع کسکانت معکوس سینوس می باشد. رویۀ یکسانی در مورد دو تابع معکوس دیگر جریان دارد. جدول 11-7 معکوس ها را در هر مورد، در شکل ساده شده، نشان می دهد. هرجا که واژۀ undefined (تعریف نشده) را می بینید، به این دلیل است که تابع اصلی دارای مقدار \(0\) است و معکوس \(0\) مقداری ندارد.

لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: