خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
معرفی توابع مثلثاتی برای تمامی زوایا

شش تابع مثلثاتی پایه همگی شروع فروتنانه ای با مثلث قائم الزاویه و زوایای آن داشتند. دایرۀ واحد (unit circle) یک دنیای کاملاً جدید را برای مقادیر ورودی در این توابع باز کرد. به خاطر ماهیت توابع مثلثاتی ـــ آنها الگوی یکسانی را دوباره و دوباره تکرار می کنند ـــ مقادیر خروجی به طور منظم ظاهر می گردند. این تکرار چیز خوبی است؛ شما تشخیص می دهید که یک ورودی خاص متعلق به کدام قسمت این الگو می باشد و سپس خروجی را تعیین می کنید.

زوایای بسیاری در مثلثات و سایر حوزه های ریاضی مورد استفاده قرار می گیرند، و اکثریت آن زوایا مضرب هایی از \(30\) و \(45\) درجه می باشند. بنابراین، اینکه یک ایده ی پنهانی داشته باشید که شما را قادر سازد از روی این لیست پرکاربرد زوایا، به سرعت به مقادیر توابع دسترسی پیدا کنید، چیز کاملاً معناداری است. به منظور تعیین تمامی توابع مثلثاتی برای تمامی زوایای، مثبت یا منفی، که مضربی از \(30\) یا \(45\) درجه باشند، که دو زاویۀ پایه ای و بنیادین هستند، تمام چیزی که لازم است بدانید یا به حافظه بسپارید، مقادیر توابع مثلثاتی برای زوایای \(0\)، \(30\)، \(45\)، و \(90\) درجه می باشد. یافتن مقادیر این توابع برای یک زاویۀ خاص یک فرایند سه مرحله ای است:
اولین گام برای یافتن مقدار تابع برای یکی از زوایایی که مضربی از \(30\) یا \(45\) درجه می باشد، اینست که زاویۀ مرجع آن را بیابیم. هنگامی که مشخص شود این زاویۀ مرجع یکی از مقادیر \(0\)، \(30\)، \(45\)، \(60\)، یا \(90\) است، شما می توانید مقدار تابع آن زاویه را مورد استفاده قرار دهید و سپس علامتش را بدست آورید (در مورد چگونگی بدست آوردن علامت در ادامه توضیح داده ایم). برای یافتن زاویۀ مرجع از جدول 1-8 یا جدول 2-8 استفاده کنید.
مقادیر سینوس برای \(30\)، \(150\)، \(210\)، و \(330\) درجه، به ترتیب عبارت از \(\frac{1}{2}\)، \(\frac{1}{2}\)، \(-\frac{1}{2}\)، و \(-\frac{1}{2}\) می باشند. تمامی این مضربهای \(30\) درجه دارای قدرمطلقی از \(\frac{1}{2}\) می باشند (همانطور که در بخش پیشین توضیح دادم). قاعدۀ زیر و شکل 1-9 به شما کمک می کنند تا تعیین کنید که آیا مقدار یک تابع مثلثاتی مثبت است یا منفی. در ابتدا، توجه داشته باشید که هر ربع صفحه در شکل با یک حرف الفبا برچسب گذاری شده است. این اعداد تصادفی نیستند؛ آنها نشان دهندۀ توابع مثلثاتی می باشند.
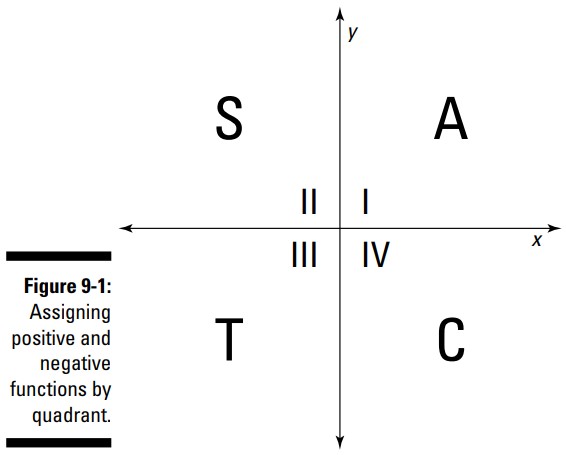
در \(QII\)، فقط سینوس و کسکانت مثبت هستند. تمامی مقادیر تابع برای زوایا در این ربع صفحه منفی هستند ـــ و این قاعده به شیوه مشابهی برای ربع صفحات دیگر ادامه می یابد.
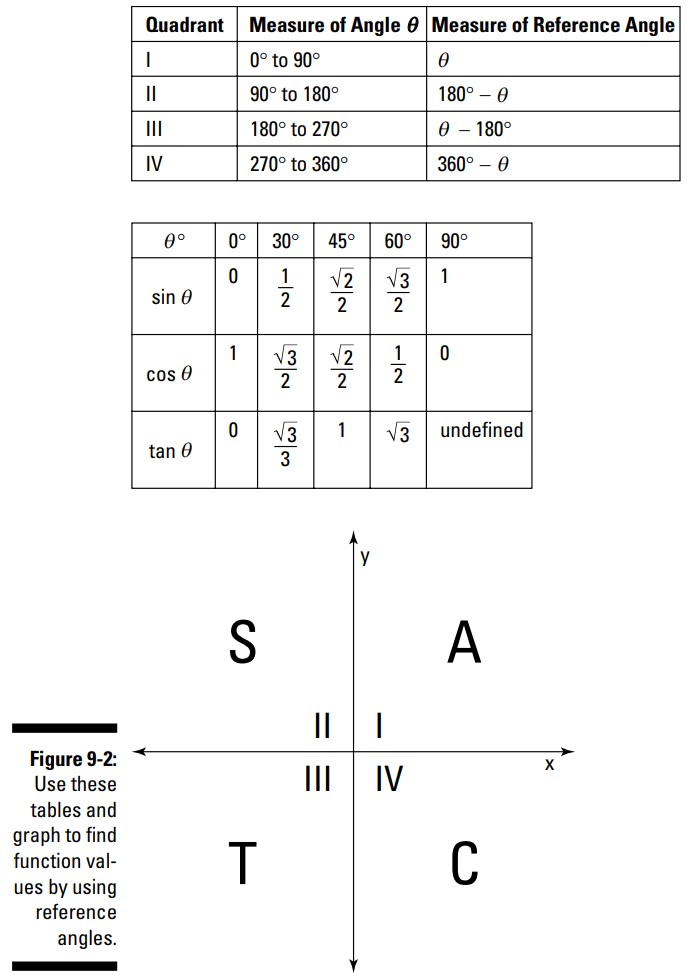
با استفاده از قوانین زوایای مرجع، مقادیر توابع برای برخی زوایای حاده (فصل 7 را ببینید)، و قانون علامت های توابع، می توانید توابع مثلثاتی را برای هر زاویه ای که در دایرۀ واحد یافت می شود، تعیین کنید ـــ هر زاویه ای که نمودارش در موقعیت استاندارد ترسیم شود (بدین معنا که رأس آن زاویه در مبدأ مختصات و ضلع آغازینش در امتداد محور \(x\) مثبت باشد). شکل 2-9 اطلاعاتی از این فصل و فصل 8 را برای شما ترکیب کرده است تا اطلاعات مورد نیازتان را به شما برساند.
حالا که به تمامی اطلاعات مورد نیاز مجهز هستید، تانژانت \(300\) درجه را بیابید.
برای اینکه با رادیان ها هم امتحان کرده باشید، کسکانت \(\frac{7\pi}{6}\) را بیابید.

معرفی توابع مثلثاتی برای تمامی زوایا
زوایای بسیاری در مثلثات و سایر حوزه های ریاضی مورد استفاده قرار می گیرند، و اکثریت آن زوایا مضرب هایی از \(30\) و \(45\) درجه می باشند. بنابراین، اینکه یک ایده ی پنهانی داشته باشید که شما را قادر سازد از روی این لیست پرکاربرد زوایا، به سرعت به مقادیر توابع دسترسی پیدا کنید، چیز کاملاً معناداری است. به منظور تعیین تمامی توابع مثلثاتی برای تمامی زوایای، مثبت یا منفی، که مضربی از \(30\) یا \(45\) درجه باشند، که دو زاویۀ پایه ای و بنیادین هستند، تمام چیزی که لازم است بدانید یا به حافظه بسپارید، مقادیر توابع مثلثاتی برای زوایای \(0\)، \(30\)، \(45\)، و \(90\) درجه می باشد. یافتن مقادیر این توابع برای یک زاویۀ خاص یک فرایند سه مرحله ای است:
-
اندازۀ زاویۀ مرجع آن زاویه را بیابید.
-
مقدار عددی صحیح را تعیین کنید.
-
تعیین کنید که آیا این مقدار تابع مثبت یا منفی است.
به کار گیریِ زاویۀ مرجع
اولین گام برای یافتن مقدار تابع برای یکی از زوایایی که مضربی از \(30\) یا \(45\) درجه می باشد، اینست که زاویۀ مرجع آن را بیابیم. هنگامی که مشخص شود این زاویۀ مرجع یکی از مقادیر \(0\)، \(30\)، \(45\)، \(60\)، یا \(90\) است، شما می توانید مقدار تابع آن زاویه را مورد استفاده قرار دهید و سپس علامتش را بدست آورید (در مورد چگونگی بدست آوردن علامت در ادامه توضیح داده ایم). برای یافتن زاویۀ مرجع از جدول 1-8 یا جدول 2-8 استفاده کنید.
تمامی زوایای دارای یک زاویۀ مرجع \(30\) درجه، دارای توابع مثلثاتی می باشند که قدرمطلقشان با مقادیر آن زاویۀ \(30\) درجه همسان است. به عنوان مثال، سینوس \(30\)، \(150\)، \(210\)، و \(330\) درجه، یا \(\frac{1}{2}\) و یا \(-\frac{1}{2}\) می باشد. به همین ترتیب، با استفاده از یک زاویۀ \(45\) درجه به عنوان یک زاویۀ مرجع، کسینوس \(45\)، \(135\)، \(225\)، و \(315\) درجه، برابر با \(\frac{\sqrt{2}}{2}\) یا \(-\frac{\sqrt{2}}{2}\) می باشد.
تعیین علامت توابع مثلثاتی برای هر ربع صفحه
مقادیر سینوس برای \(30\)، \(150\)، \(210\)، و \(330\) درجه، به ترتیب عبارت از \(\frac{1}{2}\)، \(\frac{1}{2}\)، \(-\frac{1}{2}\)، و \(-\frac{1}{2}\) می باشند. تمامی این مضربهای \(30\) درجه دارای قدرمطلقی از \(\frac{1}{2}\) می باشند (همانطور که در بخش پیشین توضیح دادم). قاعدۀ زیر و شکل 1-9 به شما کمک می کنند تا تعیین کنید که آیا مقدار یک تابع مثلثاتی مثبت است یا منفی. در ابتدا، توجه داشته باشید که هر ربع صفحه در شکل با یک حرف الفبا برچسب گذاری شده است. این اعداد تصادفی نیستند؛ آنها نشان دهندۀ توابع مثلثاتی می باشند.

دورتادور ربع صفحه ها را بخوانید، با \(QI\) آغاز کنید و به صورت پادساعت گرد پیش بروید، قوانین از این قرار هستند. اگر ضلع نهایی آن زاویه در ربع صفحۀ مشخص شده با حرف الفبای زیر باشد، قوانین اشاره شده بر روی آن صادق هستند:
-
A: تمامی توابع مثبت هستند.
-
S: سینوس و معکوس آن، کسکانت، مثبت هستند.
-
T: تانژانت و معکوس آن، کتانژانت، مثبت هستند.
-
C: کسینوس و معکوس آن، سکانت، مثبت هستند.
در \(QII\)، فقط سینوس و کسکانت مثبت هستند. تمامی مقادیر تابع برای زوایا در این ربع صفحه منفی هستند ـــ و این قاعده به شیوه مشابهی برای ربع صفحات دیگر ادامه می یابد.
معلم مثلثات من، دکتر جانسون (Dr. Johnson)، یک روش عالی برای به یاد آوری این قاعده به من نشان داد: "All Students Take Calculus" (همۀ دانش آموزان حسابان را می فهمند.)
ترکیب همۀ قواعد
با استفاده از قوانین زوایای مرجع، مقادیر توابع برای برخی زوایای حاده (فصل 7 را ببینید)، و قانون علامت های توابع، می توانید توابع مثلثاتی را برای هر زاویه ای که در دایرۀ واحد یافت می شود، تعیین کنید ـــ هر زاویه ای که نمودارش در موقعیت استاندارد ترسیم شود (بدین معنا که رأس آن زاویه در مبدأ مختصات و ضلع آغازینش در امتداد محور \(x\) مثبت باشد). شکل 2-9 اطلاعاتی از این فصل و فصل 8 را برای شما ترکیب کرده است تا اطلاعات مورد نیازتان را به شما برساند.
حالا که به تمامی اطلاعات مورد نیاز مجهز هستید، تانژانت \(300\) درجه را بیابید.
-
زاویۀ مرجع را بیابید.
با استفاده از جدول بالایی در شکل 2-9 ، می توانید ببینید که ضلع نهایی زاویۀ \(300\) درجه در ربع صفحۀ چهارم قرار دارد، بنابراین زاویۀ مرجع آن را با تفریق \(300\) از \(360\) بدست می آورید. بنابراین، اندازۀ زاویۀ مرجع برابر با \(60\) درجه می باشد.
-
مقدار عددی تانژانت را بیابید.
با استفاده از جدول میانی در شکل 2-9 می توانید مقدار عددی تانژانت \(60\) درجه را که برابر با \(\sqrt{2}\) می باشد، ببینید.
-
علامت تانژانت را بیابید.
از آنجا که یک زاویۀ \(300\) درجه در ربع صفحۀ چهارم قرار دارد، و زاویه های آن ربع صفحه دارای تانژانت های منفی می باشند (در این زمینه به بخش قبلی همین آموزش مراجعه کنید)، تانژانت \(300\) درجه، برابر با \(-\sqrt{3}\) می باشد.

برای اینکه با رادیان ها هم امتحان کرده باشید، کسکانت \(\frac{7\pi}{6}\) را بیابید.
-
زاویۀ مرجع را بیابید.
برای استفاده از جدول بالایی در شکل 2-9، شما نیاز دارید تا معادل درجۀ اندازۀ \(\frac{7\pi}{6}\) را بیابید. در فصل 5، می توانید فرمول تبدیل رادیان به درجه را بیابید. در این مورد با استفاده از این فرمول تبدیل، در می یابید که \(\frac{7\pi}{6}\) برابر با \(210^{\circ}\) می باشد. این زاویه در ربع صفحۀ سوم می باشد، پس، شما می توانید زاویۀ مرجع آن را با تفریق \(\pi\) از \(\frac{7\pi}{6}\) بدست آورید:
$$\frac{7\pi}{6}-\pi=\frac{\pi}{6}$$
-
مقدار عددی کسکانت را بیابید.
در جدول میانی شکل 2-9، کسکانت ظاهر نشده است. اگرچه، معکوس کسکانت، سینوس می باشد. بنابراین مقدار سینوس را بیابید، و معکوس آن را مورد استفاده قرار دهید. سینوس \(\frac{\pi}{6}\) برابر با \(\frac{1}{2}\) است، که بدین معناست که کسکانت \(\frac{\pi}{6}\) برابر با \(2\) می شود (معکوس آن).
-
علامت کسکانت را بیابید.
در ربع صفحۀ سوم، کسکانت یک زاویه منفی می باشد، بنابراین کسکانت \(\frac{7\pi}{6}\) برابر با \(-2\) می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: