خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
دامنه و برد توابع مثلثاتی

دامنۀ (domain) یک تابع عبارت از تمامی ورودی هایی است که یک تابع می تواند آن را به کار ببرد ـــ روشی که آن تابع معرفی شده است. مسلماً، هنگامی که مقادیر ورودی را وارد یک تابع می کنید، قصد دارید تا به مقادیر خروجی برسید، این مقادیر خروجی بُرد (range) تابع می باشند (برای اطلاعات بیشتر در مورد دامنه و برد تابع فصل 3 را ببینید). اما گاهی اوقات، هنگامی که چیزی را وارد می کنید که به آن تابع تعلق ندارد، با برخی از وضعیتهای غیرممکن مواجه می شوید. در اینگونه موارد، شما نیاز به محدود کردن مقادیر ورودی آن تابع دارید ـــ دامنۀ آن باید محدود گردد. به عنوان مثال، کسکانت به شکل وتر تقسیم بر ضلع روبرو تعریف شده است (فصل 7 را ببینید). اگر ضلع نهایی آن زاویه بر روی محور \(x\) باشد، آن گاه ضلع روبرو برابر با \(0\) خواهد بود، و از شما خواسته شده است تا آن را بر \(0\) تقسیم کنید. غیرممکن است!

توابع مثلثاتی دارای دامنه هایی می باشند که اندازۀ زوایا در واحد درجه یا واحد رادیان هستند (تمامی ورودی ها زوایا هستند). خروجی های توابع مثلثاتی اعداد حقیقی می باشند. مشکل اینست که توابع مثلثاتی مختلف دارای دامنه ها و بردهای متفاوتی می باشند. شما نمی توانید صرفاً هر زاویه ای را در هر تابعی قرار دهید. سینوس و کسینوس بسیاری همکاری می کنند و دارای دامنه و برد یکسانی می باشند. با این حال، تابع تانژانت و توابع معکوس، اینگونه نیستند. بهترین روش برای توصیف این دامنه ها و بردهای متفاوت روش بصری است: به صفحۀ مختصات همراه با یک دایره که مرکزش در مبدأ قرار دارد و یک مثلث قائم الزاویه درون آن، ارجاع کنید. این مثلث قائم الزاویه از عمود کردن یک خط از هر نقطۀ دلخواه \((x,y)\) بر روی محیط دایره، به محور \(x\) شکل گرفته است (شکل 7-9 را ببینید). یادتان باشد که \(r\) مخفف radius (شعاع دایره) می باشد (و همچنین در این شکل وتر این مثلث قائم الزاویه نیز هست). هنگامی که این وتر در امتداد یکی از محورها قرار می گیرد، یکی از اضلاع این مثلث برابر با \(0\) می گردد، که ابداً نباید در مخرج یک کسر قرار گیرد.
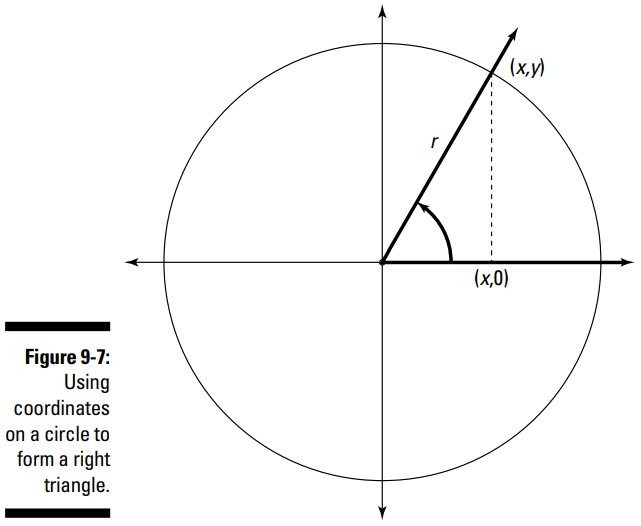
مقادیر متغیرها در شکل 7-9 را در ارتباط با یکدیگر در نظر بگیرید. شعاع، \(r\)، همواره مثبت است. و قدر مطلق \(x\) و \(y\) (طول پاره خطهایی که نشان می دهند) همواره از \(r\) کوچکتر است، مگر اینکه نقطۀ \((x,y)\) بر روی محور قرار داشته باشد ـــ آن گاه یکی از این مقادیر برابر با \(r\) و دیگری برابر با \(0\) خواهد بود.
توابع سینوس و کسینوس در دنیای توابع مثلثاتی بی همتا هستند، زیرا نسبت های آنها همواره دارای یک مقدار است. مهم نیست که چه زاویه ای را وارد این توابع کنید، در هر صورت نتیجه ای را به عنوان خروجی دریافت خواهید کرد. مقداری که بدست می آورید، ممکن است \(0\) باشد، اما به هر حال آن هم یک عدد است. در ارتباط با صفحۀ مختصات، سینوس برابر با \(\frac{y}{r}\)، و کسینوس برابر با \(\frac{x}{r}\) می باشد.
شعاع، \(r\)، همواره عددی مثبت است (به همین دلیل است که این توابع همیشه دارای یک مقدار هستند، زیرا از شما نمی خواهند تا بر \(0\) تقسیم انجام بدهید)، و \(r\) همیشه عددی بزرگتر (یا برابر با) قدر مطلق \(x\) و \(y\) می باشد.
نسبت های \(\frac{y}{r}\) و \(\frac{x}{r}\) هرگز یک کسر ناسره (improper fractions) نخواهند شد ـــ صورت آن هرگز بزرگتر از مخرجش نخواهد بود ـــ زیرا مقدار \(r\)، شعاع، همواره عدد بزرگتر است. در بهترین حالت، اگر زاویۀ \(\theta\) دارای یک ضلع نهایی بر روی یک محور باشد (بدین معنا که یکی از اضلاع آن برابر با \(r\) شود)، آن گاه مقدار آن نسبت برابر با \(1\) یا \(-1\) خواهد شد.
توابع کسکانت و سکانت ارتباط تنگاتنگی با سینوس و کسینوس دارند، زیرا معکوس یکدیگر می باشند. در ارتباط با صفحۀ مختصات، کسکانت برابر با \(\frac{r}{y}\)، و سکانت برابر با \(\frac{r}{x}\) می باشند. مقدار \(r\) طول وتر یک مثلث قائم الزاویه است ـــ که همانطور که در ابتدای این بخش دریافتید، همواره مثبت و همواره بزرگتر از \(x\) و \(y\) می باشد. تنها مشکلی که در محاسبۀ این توابع رخ می دهد، هنگامی است که \(x\) یا \(y\) برابر با \(0\) باشند ـــ هنگامیکه ضلع نهایی این زاویه بر روی یک محور باشد. یک تابع با \(0\) در مخرج آن، عدد یا مقداری را تولید می کند که وجود ندارد (به زبان ریاضی، نتیجۀ آن تعریف نشده است)، بنابراین هرگاه که \(x\) یا \(y\) برابر با \(0\) باشد، شما هیچ خروجی را از توابع کسکانت یا سکانت بدست نخواهید آورد. هنگامیکه ضلع نهایی بر روی محور \(y\) قرار گیرد، \(x\) برابر با \(0\) خواهد بود، و هنگامیکه ضلع نهایی بر روی محور \(x\) قرار گیرد، \(y\) برابر با \(0\) خواهد بود.
دامنه های کسکانت و سکانت محدود هستند ـــ شما تنها می توانید از توابعی برای اندازۀ زوایا استفاده کنید که مقدار خروجی آنها وجود داشته باشند.
نسبت های توابع کسکانت و سکانت در صفحۀ مختصات، \(\frac{r}{y}\) و \(\frac{r}{x}\)، دارای وتر، \(r\)، در صورت کسر می باشند. از آنجا که \(r\) همواره مثبت و بزرگتر یا برابر با \(x\) و \(y\) است، این کسرها همواره ناسره (بزرگتر از \(1\)) یا برابر با \(1\) می باشند. بردهای این دو تابع هرگز شامل کسرهای سره (اعداد بین \(-1\) و \(1\)) نمی گردند.
توابع تانژانت و کتانژانت نه تنها بر اساس این واقعیت که معکوس یکدیگرند، بلکه همچنین بر اساس رفتار بردهایشان با یکدیگر در ارتباطند. در ارتباط با صفحۀ مختصات، تانژانت برابر با \(\frac{y}{x}\)، و کتانژانت برابر با \(\frac{x}{y}\) می باشند. دامنۀ هر دو تابع محدود هستند، زیرا گاهی اوقات نسبتهای آنها می تواند دارای صفرهایی در مخرج کسرها باشند، اما بردهای آنها نامحدود می باشند.
هرگاه که مخرج نسبت مربوطه به \(0\) نزدیک گردد، مقادیر برد این توابع می توانند بسیار کوچک گردند (به سمت منفی بی نهایت پیش روند) یا بسیار بزرگ گردند (به سمت مثبت بی نهایت پیش روند). هنگامی که عددی را بر عدد بسیار کوچکی همچون \(0.0001\) تقسیم کنید، نتیجه عدد بزرگی می شود. هرچقدر مخرج کوچکتر باشد، نتیجه بزرگتر خواهد شد.

توابع مثلثاتی دارای دامنه هایی می باشند که اندازۀ زوایا در واحد درجه یا واحد رادیان هستند (تمامی ورودی ها زوایا هستند). خروجی های توابع مثلثاتی اعداد حقیقی می باشند. مشکل اینست که توابع مثلثاتی مختلف دارای دامنه ها و بردهای متفاوتی می باشند. شما نمی توانید صرفاً هر زاویه ای را در هر تابعی قرار دهید. سینوس و کسینوس بسیاری همکاری می کنند و دارای دامنه و برد یکسانی می باشند. با این حال، تابع تانژانت و توابع معکوس، اینگونه نیستند. بهترین روش برای توصیف این دامنه ها و بردهای متفاوت روش بصری است: به صفحۀ مختصات همراه با یک دایره که مرکزش در مبدأ قرار دارد و یک مثلث قائم الزاویه درون آن، ارجاع کنید. این مثلث قائم الزاویه از عمود کردن یک خط از هر نقطۀ دلخواه \((x,y)\) بر روی محیط دایره، به محور \(x\) شکل گرفته است (شکل 7-9 را ببینید). یادتان باشد که \(r\) مخفف radius (شعاع دایره) می باشد (و همچنین در این شکل وتر این مثلث قائم الزاویه نیز هست). هنگامی که این وتر در امتداد یکی از محورها قرار می گیرد، یکی از اضلاع این مثلث برابر با \(0\) می گردد، که ابداً نباید در مخرج یک کسر قرار گیرد.

مقادیر متغیرها در شکل 7-9 را در ارتباط با یکدیگر در نظر بگیرید. شعاع، \(r\)، همواره مثبت است. و قدر مطلق \(x\) و \(y\) (طول پاره خطهایی که نشان می دهند) همواره از \(r\) کوچکتر است، مگر اینکه نقطۀ \((x,y)\) بر روی محور قرار داشته باشد ـــ آن گاه یکی از این مقادیر برابر با \(r\) و دیگری برابر با \(0\) خواهد بود.
توابع دوست داشتنی: سینوس و کسینوس
توابع سینوس و کسینوس در دنیای توابع مثلثاتی بی همتا هستند، زیرا نسبت های آنها همواره دارای یک مقدار است. مهم نیست که چه زاویه ای را وارد این توابع کنید، در هر صورت نتیجه ای را به عنوان خروجی دریافت خواهید کرد. مقداری که بدست می آورید، ممکن است \(0\) باشد، اما به هر حال آن هم یک عدد است. در ارتباط با صفحۀ مختصات، سینوس برابر با \(\frac{y}{r}\)، و کسینوس برابر با \(\frac{x}{r}\) می باشد.
شعاع، \(r\)، همواره عددی مثبت است (به همین دلیل است که این توابع همیشه دارای یک مقدار هستند، زیرا از شما نمی خواهند تا بر \(0\) تقسیم انجام بدهید)، و \(r\) همیشه عددی بزرگتر (یا برابر با) قدر مطلق \(x\) و \(y\) می باشد.
دامنه های سینوس و کسینوس
دامنه های سینوس و کسینوس بی نهایت می باشند. به زبان مثلثات، شما چیزی شبیه این را می گویید: اگر \(\theta\) نشان دهندۀ تمامی زوایایِ دامنۀ این دو تابع باشد \(f(\theta)= \sin \theta\) و \(g(\theta)= \cos \theta\) ، آن گاه \(-\infty \lt \theta \lt \infty\)، که معنایش این می شود که \(\theta\) می تواند هر زاویه ای در واحد درجه یا واحد رادیان باشد ـــ هر عدد حقیقی.
بُردهای سینوس و کسینوس
مقادیر خروجی برای سینوس و کسینوس همیشه بین (و شامل) \(-1\) و \(1\) می باشند. به زبان مثلثات، چیزی شبیه این می شود: اگر \(f(\theta)\) و \(g(\theta)\) نشان دهندۀ مقادیر خروجی توابع \(f(\theta)=\sin \theta\) و \(g(\theta)=\cos \theta\) باشند، آن گاه \(-1 \le f(\theta) \le 1\) و \(-1 \le g(\theta) \le 1\) .
نسبت های \(\frac{y}{r}\) و \(\frac{x}{r}\) هرگز یک کسر ناسره (improper fractions) نخواهند شد ـــ صورت آن هرگز بزرگتر از مخرجش نخواهد بود ـــ زیرا مقدار \(r\)، شعاع، همواره عدد بزرگتر است. در بهترین حالت، اگر زاویۀ \(\theta\) دارای یک ضلع نهایی بر روی یک محور باشد (بدین معنا که یکی از اضلاع آن برابر با \(r\) شود)، آن گاه مقدار آن نسبت برابر با \(1\) یا \(-1\) خواهد شد.
کسکانت و سکانت
توابع کسکانت و سکانت ارتباط تنگاتنگی با سینوس و کسینوس دارند، زیرا معکوس یکدیگر می باشند. در ارتباط با صفحۀ مختصات، کسکانت برابر با \(\frac{r}{y}\)، و سکانت برابر با \(\frac{r}{x}\) می باشند. مقدار \(r\) طول وتر یک مثلث قائم الزاویه است ـــ که همانطور که در ابتدای این بخش دریافتید، همواره مثبت و همواره بزرگتر از \(x\) و \(y\) می باشد. تنها مشکلی که در محاسبۀ این توابع رخ می دهد، هنگامی است که \(x\) یا \(y\) برابر با \(0\) باشند ـــ هنگامیکه ضلع نهایی این زاویه بر روی یک محور باشد. یک تابع با \(0\) در مخرج آن، عدد یا مقداری را تولید می کند که وجود ندارد (به زبان ریاضی، نتیجۀ آن تعریف نشده است)، بنابراین هرگاه که \(x\) یا \(y\) برابر با \(0\) باشد، شما هیچ خروجی را از توابع کسکانت یا سکانت بدست نخواهید آورد. هنگامیکه ضلع نهایی بر روی محور \(y\) قرار گیرد، \(x\) برابر با \(0\) خواهد بود، و هنگامیکه ضلع نهایی بر روی محور \(x\) قرار گیرد، \(y\) برابر با \(0\) خواهد بود.
دامنه های توابع کسکانت و سکانت
دامنه های کسکانت و سکانت محدود هستند ـــ شما تنها می توانید از توابعی برای اندازۀ زوایا استفاده کنید که مقدار خروجی آنها وجود داشته باشند.
هر گاه ضلع نهایی یک زاویه در امتداد محور \(x\) قرار گرفته باشد (که در آن \(y=0\))، شما نمی توانید تابع کسکانت را بر روی آن زاویه اجرا کنید. به زبان مثلثات، این قاعده اینگونه است: اگر \(h(\theta) = \csc \theta\) ، آن گاه \(\theta \ne 0,180,360,540,...\) ، یا هر مضرب دیگری از \(180\) درجه. در واحد رادیان \(\theta \ne 0,\pi,2\pi,3\pi, ...\) یا هر مضرب دیگری از \(\pi\) .
هرگاه که ضلع نهایی یک زاویه در امتداد محور \(y\) قرار گرفته باشد (که در آن \(x=0\))، نمی توانید تابع سکانت را بر روی آن زاویه بکار ببرید. بنابراین، به زبان مثلثات، این را اینگونه بیان می دارید: اگر \(k(\theta)=\sec \theta\) آن گاه \(\theta \ne 90,270,450,630,...\) یا هر مضرب فرد دیگری از \(90\) درجه. در واحد رادیان \(\theta \ne \frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2}\frac{7\pi}{2},...\) یا هر مضرب فرد دیگری از \(\frac{\pi}{2}\) .
بُردهای توابع کسکانت و سکانت
نسبت های توابع کسکانت و سکانت در صفحۀ مختصات، \(\frac{r}{y}\) و \(\frac{r}{x}\)، دارای وتر، \(r\)، در صورت کسر می باشند. از آنجا که \(r\) همواره مثبت و بزرگتر یا برابر با \(x\) و \(y\) است، این کسرها همواره ناسره (بزرگتر از \(1\)) یا برابر با \(1\) می باشند. بردهای این دو تابع هرگز شامل کسرهای سره (اعداد بین \(-1\) و \(1\)) نمی گردند.
اگر \(h(\theta)\) و \(k(\theta)\) مقادیر خروجی توابع \(h(\theta)=\csc \theta\) و \(k(\theta)=\sec \theta\) باشند، آن گاه \(h(\theta) \le -1\) یا \(h(\theta) \ge 1\) و \(k(\theta) \le -1\) یا \(k(\theta) \ge 1\) .
تانژانت و کتانژانت
توابع تانژانت و کتانژانت نه تنها بر اساس این واقعیت که معکوس یکدیگرند، بلکه همچنین بر اساس رفتار بردهایشان با یکدیگر در ارتباطند. در ارتباط با صفحۀ مختصات، تانژانت برابر با \(\frac{y}{x}\)، و کتانژانت برابر با \(\frac{x}{y}\) می باشند. دامنۀ هر دو تابع محدود هستند، زیرا گاهی اوقات نسبتهای آنها می تواند دارای صفرهایی در مخرج کسرها باشند، اما بردهای آنها نامحدود می باشند.
دامنه های توابع تانژانت و کتانژانت
از آنجا که در تابع تانژانت \(x\) نمی تواند برابر با \(0\) باشد، این قاعده برقرار است: اگر \(m(\theta)=\tan \theta\) ، آن گاه \(\theta \ne 90,270,450,630,...\) یا هر مضرب فرد دیگری از \(90\) درجه. در واحد رادیان \(\theta \ne \frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2},\frac{7\pi}{2},...\) یا هر مضرب فرد دیگری از \(\frac{\pi}{2}\). هر دو تابع تانژانت و سکانت دارای نسبتهایی با \(x\) در مخرجشان می باشند، که منجر می شود تا دامنۀ آنها یکسان باشد.
برای اینکه تابع کتانژانت بدرستی کار کند، \(y\) نمی تواند برابر با \(0\) باشد. اگر \(n(\theta) = \cot \theta\)، آنگاه \(\theta \ne 0,180,360,540,...\) یا هر مضرب دیگری از \(180\) درجه. در واحد رادیان \(\theta \ne 0,\pi,2\pi,3\pi,...\) یا هر مضرب دیگری از \(\pi\).
بردهای توابع تانژانت و کتانژانت
برد هر دو تابع تانژانت و کتانژانت بی نهایت می باشند، که وقتیکه در نمادهای ریاضی بیان شود، اینگونه است: \(-\infty \lt m(\theta) \lt \infty\) و \(-\infty \lt n(\theta) \lt \infty\) .
هرگاه که مخرج نسبت مربوطه به \(0\) نزدیک گردد، مقادیر برد این توابع می توانند بسیار کوچک گردند (به سمت منفی بی نهایت پیش روند) یا بسیار بزرگ گردند (به سمت مثبت بی نهایت پیش روند). هنگامی که عددی را بر عدد بسیار کوچکی همچون \(0.0001\) تقسیم کنید، نتیجه عدد بزرگی می شود. هرچقدر مخرج کوچکتر باشد، نتیجه بزرگتر خواهد شد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: