خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
اتحادهای فیثاغورثی

فیثاغورث خوب و قدیمی همه جا در کار است ـــ قضیۀ او در عجیب ترین مکان ها ظاهر می شود. (مسلماً منظور من این نیست که یک فصل در این کتاب جای عجیبی است.) این بخش شما را به ماورای چیزهای پایه ای می برد، و آنها را با سه اتحاد که اتحادهای فیثاغورثی (Pythagorean identities) نامیده می شود، گسترش می دهد. (برای اطلاعات بیشتر در مورد قضیۀ فیثاغورث، به فصل های 2 و 6 مراجعه کنید.)

اتحادهای فیثاغورثی بلوک های سازندۀ بسیاری از دستکاری های معادلات و عبارات می باشند. آنها تعداد زیادی روش برای حل کردن مسأله ها به صورت کارآمدتر فراهم می کنند، زیرا به شما امکان می دهند تا عبارتهای پیچیده را در شکلهای بسیار ساده تر بنویسید.
اتحاد فیثاغورثی اصلی که آن دو اتحاد دیگر را به دنیا آورده است \(\sin^2 \theta + \cos^2 \theta = 1\) می باشد. اما ممکن است با خودتان بیندیشید، این اتحاد از کجا آمده است، و چرا اینقدر مهم است؟ سوال آخر را اول جواب می دهم: دلیل اهمیت اتحاد فیثاغورثی اصلی اینست که ترکیبی از توابع را برابر با \(1\) قرار می دهد، و این ساده سازی برای حل کردن معادلات مثلثاتی سودمند می باشد. همینطور، این یکی از پرکاربردترین اتحادها از بین همۀ آنها می باشد. این اتحاد نتیجۀ قرار دادن یک مثلث قائم الزاویه درون دایرۀ واحد و جایگذاری مقادیر و معادلات برای رسیدن به یک معادلۀ کاملاً جدید می باشد (شکل 3-11 را ببینید).
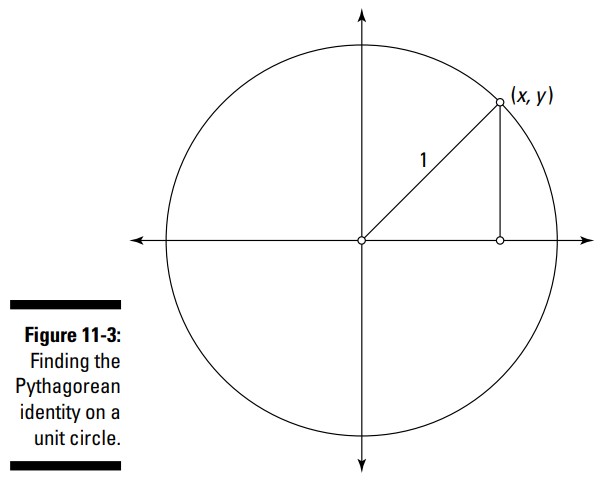
در فصل 9 دریافتید که در یک دایره، \(\sin \theta = \frac{y}{r}\) و \(\cos \theta = \frac{x}{r}\)، که در آن \((x,y)\) مختصات های این نقطه و \(r\) شعاع این دایره می باشد. همچنین مقدار \(x\) طول ضلع مجاور این مثلث (طول افقی) نیز می باشد، و \(y\) طول ضلع روبرو (طول عمودی) می باشد. در یک دایرۀ واحد، شعاع برابر با \(1\) است. هنگامی که \(1\) را در این معادله جایگزین \(r\) می کنید، به نتیجۀ \(\sin \theta = \frac{y}{1} = y\) و \(\cos \theta = \frac{x}{1}=x\) می رسید. این نتیجه گیری یادتان باشد، تا دوباره از آن استفاده کنیم.
قضیۀ فیثاغورث بیان می دارد که هنگامی که مقدار دو ساق یک مثلث قائم الزاویه را مربع می سازید و نتایج آن را با هم جمع می زنید، به مربع وتر می رسید. در نماد ریاضی، اینگونه است: \(a^2+b^2=c^2\) . در مورد مثلث قائم الزاویۀ قرار گرفته در دایرۀ واحد از آنجا که شعاع (که همچنین وتر نیز می باشد) برابر با \(1\) است، شما می توانید بگویید که \(x^2+y^2=1^2\) . اکنون این \(x\) را با \(\cos \theta\) و این \(y\) را با \(\sin \theta\) جایگزین کنید، این دو عبارت را با یکدیگر جابجا کنید، و به نتیجۀ \(\sin^2 \theta + \cos^2 \theta = 1\) می رسید.
این اتحاد را در عمل بررسی کنید. فرض کنید اندازۀ زاویه در سوال برابر با \(30\) درجه باشد. با استفاده از مقادیر این توابع برای یک زاویۀ \(30\) درجه (ضمیمۀ کتاب را ببینید)، \(\sin 30^{\circ} = \frac{1}{2}\) و \(\cos 30^{\circ} = \frac{\sqrt{3}}{2}\)، و جایگذاری آنها در این اتحاد، به نتیجۀ زیر می رسید:
$$
\sin^2 \theta + \cos^2 \theta = 1 \\
\biggl( \frac{1}{2} \biggr)^2 + \biggl( \frac{\sqrt{3}}{2} \biggr)^2 = \frac{1}{4} + \frac{3}{4}=1
$$
دو اتحاد فیثاغورثی دیگر که از اتحاد اول که شامل سینوس و کسینوس می باشد، منتج شده اند. تمام کاری که باید انجام دهید افزودن اندکی جبر، به کار بردن اتحاد معکوس و اتحاد نسبت (این دو اتحاد را پیشتر در همین فصل بررسی کردیم)، ساده سازی، و اثبات، می باشد! ـــ دو اتحاد جدید نتیجه می شود.
اگر بخش قبلی را خوانده باشید، می توانید به سادگی آن عملکرد را با کتانژانت و کسکانت تکرار کنید. در اینجا چگونگی این کار را می بینید:
بخش های پیشین تعاریف اصلی اتحادهای فیثاغورثی را نشان دادند، اما همانطور که خودتان هم گمان کرده بودید، این اشکال در اینجا خاتمه نمی یابند. آشنا شدن با سایر نسخه های این اتحادها به نحویکه در هنگام حل کردن معادلات یا ساده سازی عبارات به سادگی آنها را شناسایی کنید، سودمند است.
شما می توانید این اتحاد فیثاغورثی اصلی را به روشهای بیشماری تغییر بدهید. برای شروع، شما می توانید هر کدام از \(\sin^2 \theta\) یا \(\cos^2 \theta\) را با تفریق جملۀ دیگر، در یک سمت این معادله منزوی کنید:
$$
\sin^2 \theta = 1 - \cos^2 \theta \\
\cos^2 \theta = 1 - \sin^2 \theta
$$
در ادامه، می توانید سمت راست هر کدام از این معادلات را فاکتورگیری کنید زیرا آن سمت تفاضل بین دو مربع کامل می باشد:
$$
\sin^2 \theta = 1 - \cos^2 \theta = (1 - \cos \theta)(1 + \cos \theta) \\
\cos^2 \theta = 1 - \sin^2 \theta = (1-\sin \theta)(1 + \sin \theta)
$$
با این وجود، گاهی اوقات، وجود یک عبارت برای \(\sin \theta\) یا \(\cos \theta\)، که در آنها این توابع مربع نشده اند، سودمند است. با آغاز کردن با نسخه قبلی اتحاد فیثاغورثی اصلی، که در آن یک تابع منزوی شده است، شما می توانید جذر هر سمت را بگیرید تا به نتایج زیر برسید:
$$
\sin \theta = \pm \sqrt{1-\cos ^2 \theta} \\
\cos \theta = \pm \sqrt{1- \sin^2 \theta}
$$
شما همچنین می توانید این دومین اتحاد فیثاغورثی را به شیوه های مختلفی تغییر دهید. با حل کردن آن برای بدست آوردن \(\tan^2 \theta\) با تفریق \(1\) از هر سمت این معادله، به نتیجۀ زیر می رسید:
$$\tan^2 \theta = \sec^2 \theta - 1$$
سپس، تفاضل بین دو مربع را در سمت راست این معادله، فاکتورگیری کنید، به نتیجۀ زیر می رسید:
$$\tan^2 \theta = \sec^2 \theta - 1 = (\sec \theta - 1)(\sec \theta + 1)$$
در پایان، با نسخۀ قبلی شروع کنید و جذر هر سمت را بگیرید، به نتیجۀ زیر می رسید:
$$\tan \theta = \pm \sqrt{\sec^2 \theta - 1}$$
رویکرد دیگری را روی این اتحاد فیثاغورثی بکار بگیرید، شما می توانید \(\tan^2 \theta\) را از هر سمت این معادله تفریق کنید و حاصل را فاکتورگیری کنید تا به نتیجۀ زیر برسید:
$$1 = \sec^2 \theta - \tan^2 \theta = (\sec \theta - \tan \theta)(\sec \theta + \tan \theta)$$
انتخابهای سازماندهی مجدد همیشه بستگی به این دارد که چه کاری می خواهید با آن جملات انجام دهید ـــ چه توابع دیگری با این مسأله در تعامل هستند.
شما می توانید آخرین اتحاد فیثاغورثی را نیز با تفریق \(1\) از هر دو سمت معادلۀ آن یا با تفریق \(\cot^2 \theta\) از هر سمت معادله، بازچینش کنید. دو نسخۀ جدید اینگونه خواهند بود:
$$
\cot^2 \theta = \csc^2 \theta - 1 \\
1 = \csc^2 \theta - \cot^2 \theta
$$
هر کدام از معادلات پیشین دارای تفاضلی از دو مربع کامل می باشند، که می تواند فاکتورگیری شود:
$$
\cot^2 \theta = \csc^2 \theta - 1 = (\csc \theta - 1)(\csc \theta + 1) \\
1 = \csc^2 \theta - \cot^2 \theta = (\csc \theta - \cot \theta)(\csc \theta + \cot \theta)
$$
و در آخر، جذر هر دو سمت این معادله منتج به یک اتحاد شامل \(\cot \theta\) می شود:
$$\cot \theta = \pm \sqrt{\csc^2 \theta - 1}$$

اتحادهای فیثاغورثی بلوک های سازندۀ بسیاری از دستکاری های معادلات و عبارات می باشند. آنها تعداد زیادی روش برای حل کردن مسأله ها به صورت کارآمدتر فراهم می کنند، زیرا به شما امکان می دهند تا عبارتهای پیچیده را در شکلهای بسیار ساده تر بنویسید.
اتحادهای فیثاغورثی عبارتند از:
$$
\sin^2 \theta + \cos^2 \theta = 1 \\
\tan^2 \theta + 1 = \sec^2 \theta \\
1 + \cot^2 \theta = \csc^2 \theta
$$
$$
\sin^2 \theta + \cos^2 \theta = 1 \\
\tan^2 \theta + 1 = \sec^2 \theta \\
1 + \cot^2 \theta = \csc^2 \theta
$$
این نماد توان که در این اتحادها مورد استفاده قرار گرفته است مخصوص مثلثات می باشد. عبارت \(\sin^2 \theta\) در واقع به معنای \((\sin \theta)^2\) می باشد، که بیان می کند، "سینوس زاویۀ \(\theta\) را پیدا کنید و سپس آن عدد را مربع سازید." اما ریاضیدانان از هدر دادن وقت و انرژی متنفر هستند، و آن پرانتزهای بزرگ دست و پا گیرِ پیرامون "\(\sin \theta\)" را کنار گذاشتند. بنابراین بر روی یک نسخۀ متراکم تر توافق کردند: بالانویسِ \(2\) درست بعد از \(\sin\) بدین معناست که شما کل عبارت را مربع می سازید. همچنین نماد یکسانی در مورد سایر توابع مثلثاتی بکار می رود (\(\cos^2 \theta\)، \(\tan^2 \theta\)، \(\cot^2 \theta\)، و به همین ترتیب).
مادر تمامی اتحادهای فیثاغورثی
اتحاد فیثاغورثی اصلی که آن دو اتحاد دیگر را به دنیا آورده است \(\sin^2 \theta + \cos^2 \theta = 1\) می باشد. اما ممکن است با خودتان بیندیشید، این اتحاد از کجا آمده است، و چرا اینقدر مهم است؟ سوال آخر را اول جواب می دهم: دلیل اهمیت اتحاد فیثاغورثی اصلی اینست که ترکیبی از توابع را برابر با \(1\) قرار می دهد، و این ساده سازی برای حل کردن معادلات مثلثاتی سودمند می باشد. همینطور، این یکی از پرکاربردترین اتحادها از بین همۀ آنها می باشد. این اتحاد نتیجۀ قرار دادن یک مثلث قائم الزاویه درون دایرۀ واحد و جایگذاری مقادیر و معادلات برای رسیدن به یک معادلۀ کاملاً جدید می باشد (شکل 3-11 را ببینید).

در فصل 9 دریافتید که در یک دایره، \(\sin \theta = \frac{y}{r}\) و \(\cos \theta = \frac{x}{r}\)، که در آن \((x,y)\) مختصات های این نقطه و \(r\) شعاع این دایره می باشد. همچنین مقدار \(x\) طول ضلع مجاور این مثلث (طول افقی) نیز می باشد، و \(y\) طول ضلع روبرو (طول عمودی) می باشد. در یک دایرۀ واحد، شعاع برابر با \(1\) است. هنگامی که \(1\) را در این معادله جایگزین \(r\) می کنید، به نتیجۀ \(\sin \theta = \frac{y}{1} = y\) و \(\cos \theta = \frac{x}{1}=x\) می رسید. این نتیجه گیری یادتان باشد، تا دوباره از آن استفاده کنیم.
قضیۀ فیثاغورث بیان می دارد که هنگامی که مقدار دو ساق یک مثلث قائم الزاویه را مربع می سازید و نتایج آن را با هم جمع می زنید، به مربع وتر می رسید. در نماد ریاضی، اینگونه است: \(a^2+b^2=c^2\) . در مورد مثلث قائم الزاویۀ قرار گرفته در دایرۀ واحد از آنجا که شعاع (که همچنین وتر نیز می باشد) برابر با \(1\) است، شما می توانید بگویید که \(x^2+y^2=1^2\) . اکنون این \(x\) را با \(\cos \theta\) و این \(y\) را با \(\sin \theta\) جایگزین کنید، این دو عبارت را با یکدیگر جابجا کنید، و به نتیجۀ \(\sin^2 \theta + \cos^2 \theta = 1\) می رسید.
این اتحاد را در عمل بررسی کنید. فرض کنید اندازۀ زاویه در سوال برابر با \(30\) درجه باشد. با استفاده از مقادیر این توابع برای یک زاویۀ \(30\) درجه (ضمیمۀ کتاب را ببینید)، \(\sin 30^{\circ} = \frac{1}{2}\) و \(\cos 30^{\circ} = \frac{\sqrt{3}}{2}\)، و جایگذاری آنها در این اتحاد، به نتیجۀ زیر می رسید:
$$
\sin^2 \theta + \cos^2 \theta = 1 \\
\biggl( \frac{1}{2} \biggr)^2 + \biggl( \frac{\sqrt{3}}{2} \biggr)^2 = \frac{1}{4} + \frac{3}{4}=1
$$
بسط دادن به تانژانت و سکانت
دو اتحاد فیثاغورثی دیگر که از اتحاد اول که شامل سینوس و کسینوس می باشد، منتج شده اند. تمام کاری که باید انجام دهید افزودن اندکی جبر، به کار بردن اتحاد معکوس و اتحاد نسبت (این دو اتحاد را پیشتر در همین فصل بررسی کردیم)، ساده سازی، و اثبات، می باشد! ـــ دو اتحاد جدید نتیجه می شود.
-
با اولین اتحاد فیثاغورثی، \(\sin^2 \theta + \cos^2 \theta = 1\) ، کار را آغاز کنید، هر جمله را بر \(\cos^2 \theta\) تقسیم کنید.
$$\frac{\sin^2 \theta}{\cos^2 \theta} + \frac{\cos^2 \theta}{\cos^2 \theta}=\frac{1}{\cos^2 \theta}$$
-
هر جمله را با استفاده از قوانین توان بازنویسی کنید \(\biggl( \frac{a^2}{b^2} \biggr) = \biggl( \frac{a}{b} \biggr)^2\) .
توجه کنید که چگونه توان \(2\) از پرانتز بیرون کشیده می شود:
$$\biggl( \frac{\sin \theta}{\cos \theta} \biggr)^2 + \biggl( \frac{\cos \theta}{\cos \theta} \biggr)^2 = \biggl( \frac{1}{\cos \theta} \biggr)^2$$
-
هر کدام از این جملات را با یک عبارت معادل آن جایگزین کنید.
-
از یک اتحاد نسبت (ratio identity)، \(\frac{\sin \theta}{\cos \theta} = \tan \theta\)، برای جایگزینی جملۀ اول با \(\tan \theta\) استفاده کنید.
-
جملۀ دوم را با \(1\) جایگزین کنید: \(\frac{\cos \theta}{\cos \theta}=1\) .
-
از یک اتحاد معکوس (reciprocal identity)، \(\frac{1}{\cos \theta} = \sec \theta\) ، استفاده کنید، تا جملۀ سوم را با \(\sec \theta\) جایگزین کنید.
با جایگذاری این عبارت در معادله و ساده سازی، به نتیجۀ زیر می رسید:
$$
(\tan \theta)^2 + (1)^2 = (\sec \theta)^2 \\
\tan^2 \theta + 1 = \sec^2 \theta
$$
این دومین اتحاد فیثاغورثی می باشد.
-
از یک اتحاد نسبت (ratio identity)، \(\frac{\sin \theta}{\cos \theta} = \tan \theta\)، برای جایگزینی جملۀ اول با \(\tan \theta\) استفاده کنید.
بسط دادن به کتانژانت و کسکانت
اگر بخش قبلی را خوانده باشید، می توانید به سادگی آن عملکرد را با کتانژانت و کسکانت تکرار کنید. در اینجا چگونگی این کار را می بینید:
-
با اولین اتحاد فیثاغورثی، \(\sin^2 \theta + \cos^2 \theta = 1\) ، آغاز کنید، هر جمله را بر \(\sin^2 \theta\) تقسیم کنید.
$$\frac{\sin^2 \theta}{\sin^2 \theta} + \frac{\cos^2 \theta}{\sin^2 \theta}=\frac{1}{\sin^2 \theta}$$
-
هر جمله را با استفاده از قوانین توان بازنویسی کنید: \(\biggl( \frac{a^2}{b^2} \biggr) = \biggl( \frac{a}{b} \biggr)^2\) .
$$\biggl( \frac{\sin \theta}{\sin \theta} \biggr)^2 + \biggl( \frac{\cos \theta}{\sin \theta} \biggr)^2 = \biggl( \frac{1}{\sin \theta} \biggr)^2 $$
-
هر کدام از جملات را با یک عبارت معادلش جایگزین کنید.
-
اولین جمله را با \(1\) جایگزین کنید: \(\frac{\sin \theta}{\sin \theta}=1\)
-
با استفاده از یک اتحاد نسبت، \(\frac{\cos \theta}{\sin \theta}=\cot \theta\)، جملۀ دوم را با \(\cot \theta\) جایگزین کنید.
-
با استفاده از یک اتحاد معکوس، \(\frac{1}{\sin \theta}=\csc \theta\)، سومین جمله را با \(\csc \theta\) جایگزین کنید.
با جایگذاری این عبارات در این معادله و ساده سازی، به نتایج زیر می رسید:
$$
(1)^2 + (\cot \theta)^2 =(\csc \theta)^2 \\
1 + \cot^2 \theta = \csc^2 \theta
$$
و در اینجا آخرین اتحاد فیثاغورثی را دارید.
-
اولین جمله را با \(1\) جایگزین کنید: \(\frac{\sin \theta}{\sin \theta}=1\)
بازچینش اتحادهای فیثاغورثی
بخش های پیشین تعاریف اصلی اتحادهای فیثاغورثی را نشان دادند، اما همانطور که خودتان هم گمان کرده بودید، این اشکال در اینجا خاتمه نمی یابند. آشنا شدن با سایر نسخه های این اتحادها به نحویکه در هنگام حل کردن معادلات یا ساده سازی عبارات به سادگی آنها را شناسایی کنید، سودمند است.
تمامی این نسخه های متفاوت جایگاه خودشان را در کاربردهای مثلثات، حسابان، یا سایر موضوعات ریاضی دارند. شما نیازی ندارید تا آنها را حفظ کنید، زیرا اگر صرفاً سه اتحاد فیثاغورثی اصلی را به خاطر داشته باشید، می توانید آنها را برای بدست آوردن چیزهایی که می خواهید حل کنید.
تغییر دادنِ \(\sin^2 \theta + \cos^2 \theta = 1\)
شما می توانید این اتحاد فیثاغورثی اصلی را به روشهای بیشماری تغییر بدهید. برای شروع، شما می توانید هر کدام از \(\sin^2 \theta\) یا \(\cos^2 \theta\) را با تفریق جملۀ دیگر، در یک سمت این معادله منزوی کنید:
$$
\sin^2 \theta = 1 - \cos^2 \theta \\
\cos^2 \theta = 1 - \sin^2 \theta
$$
در ادامه، می توانید سمت راست هر کدام از این معادلات را فاکتورگیری کنید زیرا آن سمت تفاضل بین دو مربع کامل می باشد:
$$
\sin^2 \theta = 1 - \cos^2 \theta = (1 - \cos \theta)(1 + \cos \theta) \\
\cos^2 \theta = 1 - \sin^2 \theta = (1-\sin \theta)(1 + \sin \theta)
$$
با این وجود، گاهی اوقات، وجود یک عبارت برای \(\sin \theta\) یا \(\cos \theta\)، که در آنها این توابع مربع نشده اند، سودمند است. با آغاز کردن با نسخه قبلی اتحاد فیثاغورثی اصلی، که در آن یک تابع منزوی شده است، شما می توانید جذر هر سمت را بگیرید تا به نتایج زیر برسید:
$$
\sin \theta = \pm \sqrt{1-\cos ^2 \theta} \\
\cos \theta = \pm \sqrt{1- \sin^2 \theta}
$$
تغییر دادنِ \(\tan^2 \theta + 1 = \sec^2 \theta\)
شما همچنین می توانید این دومین اتحاد فیثاغورثی را به شیوه های مختلفی تغییر دهید. با حل کردن آن برای بدست آوردن \(\tan^2 \theta\) با تفریق \(1\) از هر سمت این معادله، به نتیجۀ زیر می رسید:
$$\tan^2 \theta = \sec^2 \theta - 1$$
سپس، تفاضل بین دو مربع را در سمت راست این معادله، فاکتورگیری کنید، به نتیجۀ زیر می رسید:
$$\tan^2 \theta = \sec^2 \theta - 1 = (\sec \theta - 1)(\sec \theta + 1)$$
در پایان، با نسخۀ قبلی شروع کنید و جذر هر سمت را بگیرید، به نتیجۀ زیر می رسید:
$$\tan \theta = \pm \sqrt{\sec^2 \theta - 1}$$
رویکرد دیگری را روی این اتحاد فیثاغورثی بکار بگیرید، شما می توانید \(\tan^2 \theta\) را از هر سمت این معادله تفریق کنید و حاصل را فاکتورگیری کنید تا به نتیجۀ زیر برسید:
$$1 = \sec^2 \theta - \tan^2 \theta = (\sec \theta - \tan \theta)(\sec \theta + \tan \theta)$$
انتخابهای سازماندهی مجدد همیشه بستگی به این دارد که چه کاری می خواهید با آن جملات انجام دهید ـــ چه توابع دیگری با این مسأله در تعامل هستند.
تغییر دادنِ \(1 + \cot^2 \theta = \csc^2 \theta\)
شما می توانید آخرین اتحاد فیثاغورثی را نیز با تفریق \(1\) از هر دو سمت معادلۀ آن یا با تفریق \(\cot^2 \theta\) از هر سمت معادله، بازچینش کنید. دو نسخۀ جدید اینگونه خواهند بود:
$$
\cot^2 \theta = \csc^2 \theta - 1 \\
1 = \csc^2 \theta - \cot^2 \theta
$$
هر کدام از معادلات پیشین دارای تفاضلی از دو مربع کامل می باشند، که می تواند فاکتورگیری شود:
$$
\cot^2 \theta = \csc^2 \theta - 1 = (\csc \theta - 1)(\csc \theta + 1) \\
1 = \csc^2 \theta - \cot^2 \theta = (\csc \theta - \cot \theta)(\csc \theta + \cot \theta)
$$
و در آخر، جذر هر دو سمت این معادله منتج به یک اتحاد شامل \(\cot \theta\) می شود:
$$\cot \theta = \pm \sqrt{\csc^2 \theta - 1}$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: