خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ترسیم نمودار تابع سینوس

نمودار تابع سینوس یک موج زیبا و پیوسته است که به نرمی در امتداد مسیر می چرخد و خودش را تکرار می کند. دامنه یا مقادیر \(x\) تابع سینوس، شامل تمامی زوایا در واحد درجه یا تمامی اعداد حقیقی در واحد رادیان می باشد، بنابراین این منحنی هیچگونه شکستگی یا سوراخی ندارد. بُرد یا مقادیر \(y\) تابع سینوس، عبارت از تمامی اعداد بین \(-1\) و \(1\) ، و خود این دو عدد، می باشد. شکل 1-19 نموداری از یک تابع سینوس را نشان می دهد که از حدود \(-2\pi\) تا \(2\pi\) (یا از حدود \(-360\) تا \(360\)) را نشان می دهد.

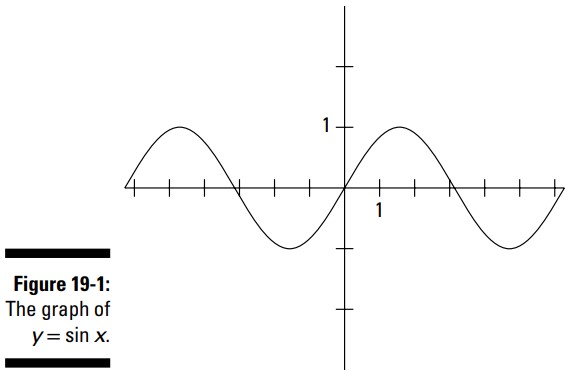
شکل 1-19 دو چرخۀ کامل از منحنی سینوس را نشان می دهد ـــ این منحنی روند خودش را دوبار در این نمودار نشان می دهد. اگر بتوانید منحنی این سینوس را تا ابد در هر دو جهت ببینید، هیچ تفاوتی نخواهد داشت. این منحنی الگوی یکسانی را بارها و بارها تا بی نهایت و ورای آن، تکرار می کند.
تابع سینوس و هر دگرگونی دیگرِ آن دارای دو ویژگی مهم می باشد: دامنۀ نوسان و دورۀ تناوبِ منحنیِ آن. شما می توانید با نگاه کردن به نمودار آن تابع یا معادلۀ آن، این ویژگیها را تعیین کنید.
دامنۀ نوسانِ تابع سینوس برابر با فاصلۀ بین مقدار میانی یا خطی است که از وسط این نمودار تا بالاترین نقطۀ آن عبور می کند. به عبارت دیگر، دامنۀ نوسان برابر با نصف مسافت پایین ترین مقدار تا بالاترین مقدار می باشد. در معادلات سینوس و کسینوس، این دامنۀ نوسان برابر با ضریب سینوس یا کسینوس می باشد. به عنوان مثال، دامنۀ نوسان در معادلۀ \(y=\sin x \) برابر با \(1\) است. برای تغییر دادن دامنۀ نوسان، تابع سینوس را در عددی ضرب کنید. در شکل 2-19 نمودار \(y=3 \sin x\) و \(y=\frac{1}{2} = \sin x\) را می بینید.
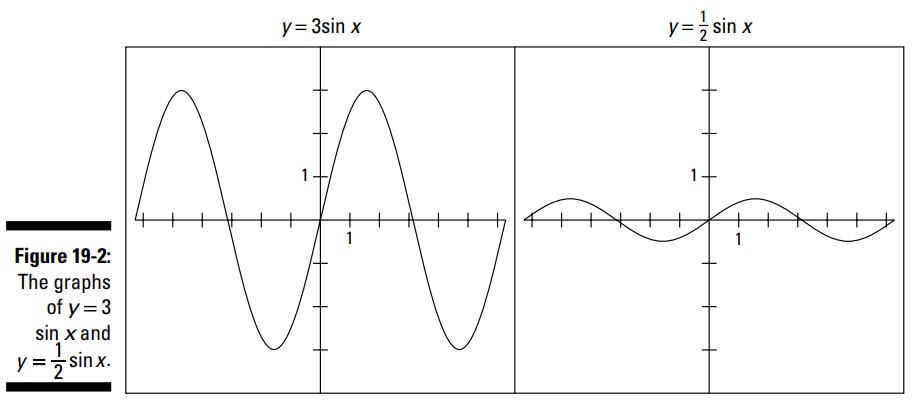
همانطور که می بینید، ضرب کردن در عددی بزرگتر از \(1\) منجر می شود تا نمودار بالاتر و پایینتر برود. دامنۀ نوسان در \(y=3 \sin x \) برابر با \(3\) می باشد. برعکس، ضرب کردن در عددی کوچکتر از \(1\) (اما بزرگتر از \(0\)) منجر می شود مقدار نمودار کوچکتر شود ـــ از آنجا بالاتر یا پایینتر نرود. دامنۀ نوسان در \(y=\frac{1}{2} \sin x\) برابر با \(\frac{1}{2}\) می باشد.
دورۀ تناوب (period) یک تابع میزان مقادیر ورودی است که منجر می شود آن تابع از تمامی مقادیر ممکن عبور کند و دوباره به نقطۀ آغازینی برسد تا این فرآیند را تکرار نماید. در مورد تابع سینوس، دورۀ تناوب برابر با \(2\pi\) یا \(360\) درجه می باشد. هر نقطه دلخواهی را بر روی منحنی سینوس انتخاب کنید، آن منحنی را به سمت راست یا چپ دنبال کنید، و در فاصلۀ \(2\pi\) یا \(360\) درجه، در امتداد محور \(x\)، از نقطه ای که آغاز کرده بودید، منحنی الگویش را دوباره تکرار می کند.
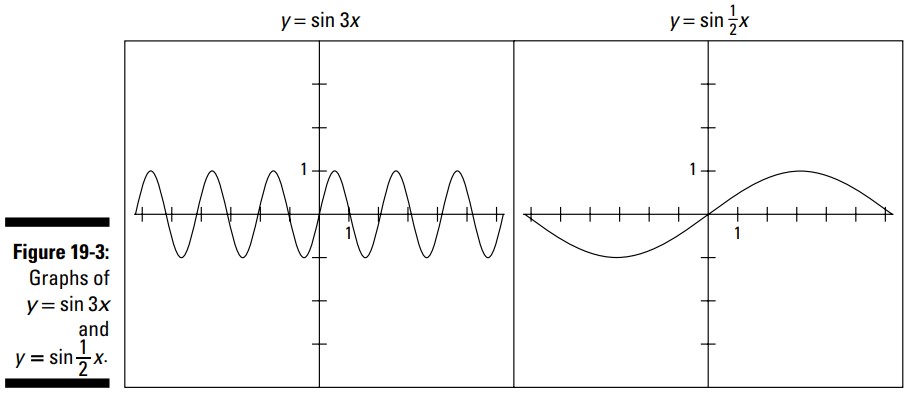
ضرب کردن متغیر زاویه، \(x\)، در یک عدد، دورۀ تناوب آن تابع را تغییر می دهد. اگر شما متغیر زاویه را در \(3\) ضرب کنید، مانند \(y=\sin 3x\)، سپس آن منحنی در مقدار فضای معمول، سه مرتبه تکمیل می شود. بنابراین، ضرب کردن در \(3\) در واقع طول دورۀ تناوب را کاهش می دهد. در مورد \(y=\sin \frac{1}{2}x\)، تنها نیمی از منحنی در همان فضا می گنجد. بنابراین، ضریبی کوچکتر از \(1\) مقدار ورودی هایی که آن تابع برای تکمیل یک چرخه نیاز دارد، افزایش می دهد. شکل 3-19 این دو نمودار نشان می دهد.
یک معادلۀ عمومی برای تابع سینوس برابر با \(y=A \sin B(x+C)+D\) می باشد. \(A\) و \(B\) اعدادی هستند که به ترتیب بر روی دامنۀ نوسان و دورۀ تناوبِ تابع اصلی سینوس تاثیر می گذارند. \(C\) و \(D\) در مکان های آغازین و پایانی جایجایی ایجاد می کنند و حتی می توانند منجر شوند این منحنی محور \(x\) را ترک کند. (در ادامۀ همین فصل در این مورد بیشتر بحث خواهیم کرد.) هنگامی که \(C\) و \(D\) هر دو برابر با صفر باشند، شما تابع اصلی سینوس را خواهید داشت: \(y=A \sin Bx\) .
با حفظ کردن این دو مقدار، می توانید به سرعت نمودار منحنی اصلی سینوس را ترسیم کنید ـــ یا آن را در ذهنتان تجسم کنید. به عنوان مثال، هنگام ترسیم نمودار \(y=4 \sin 2x\) :

شما می توانید با دامنۀ نوسان و دورۀ تناوب منحنی سینوس بازی کنید و نتیجه اش تغییرات جالبی در منحنی اصلی خواهد بود. با این حال، آن منحنی هنوز هم قابل تشخیص خواهد بود. شما هنوز هم می توانید منحنی های نرمی را که با چرخش از یک خط میانی بالا و پایین می روند را ببینید. علاوه بر این تغییرات، شما دو گزینۀ دیگر برای تغییر منحنی سینوس دارید ـــ انتقال منحنی به سمت بالا، پایین، یا پهلوها. این تغییر مکان ها انتقال (translations) آن منحنی نامیده می شوند. (برای مشاهدۀ یک بحث اولیه در مورد انتقال توابع می توانید فصل 3 را مرور کنید.) و این انتقال ها در معادلۀ عمومی تر سینوس لحاظ شده اند: \(y=A \sin B(x+C)+D\) .
شما می توانید به سادگی با افزودن یا تفریق یک عدد در معادلۀ منحنی یک سینوس، آن منحنی را به سمت بالا یا پایین منتقل کنید. به لحاظ این معادله، اگر \(D\) عددی مثبت باشد، شما آن منحنی را به آن میزان به بالا منتقل می کنید؛ اگر \(D\) عددی منفی باشد، منحنی به سمت پایین منتقل می گردد. به عنوان مثال، نمودار \(y=\sin x + 4\) کل منحنی را \(4\) واحد به سمت بالا منتقل می کند، و منحنی سینوس از خط \(y=4\) به سمت بالا و پایینش عبور می کند. از سوی دیگر، نمودار \(y=\sin x-1\) همه چیز را \(1\) واحد به سمت پایین منتقل می کند. شکل 5-19 این دو نمودار را به شما نشان می دهد.
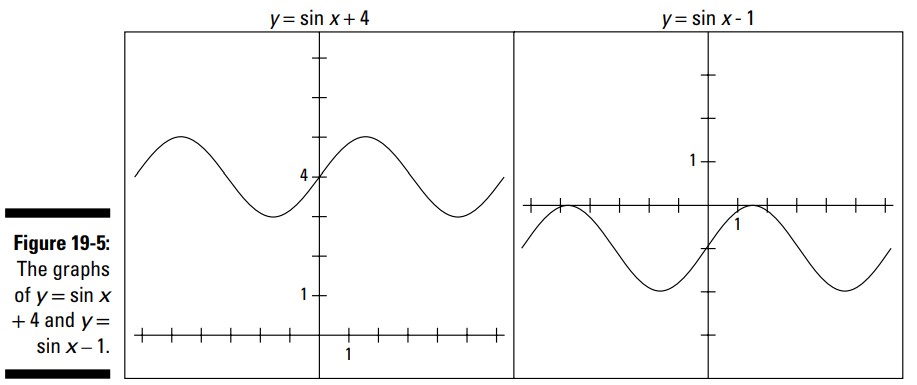
همانطور که می توانید ببینید، شکل اصلی منحنی سینوس هنوز هم قابل تشخیص است ـــ صرفاً منحنی ها در صفحۀ مختصات به سمت بالا یا پایین منتقل شده اند.
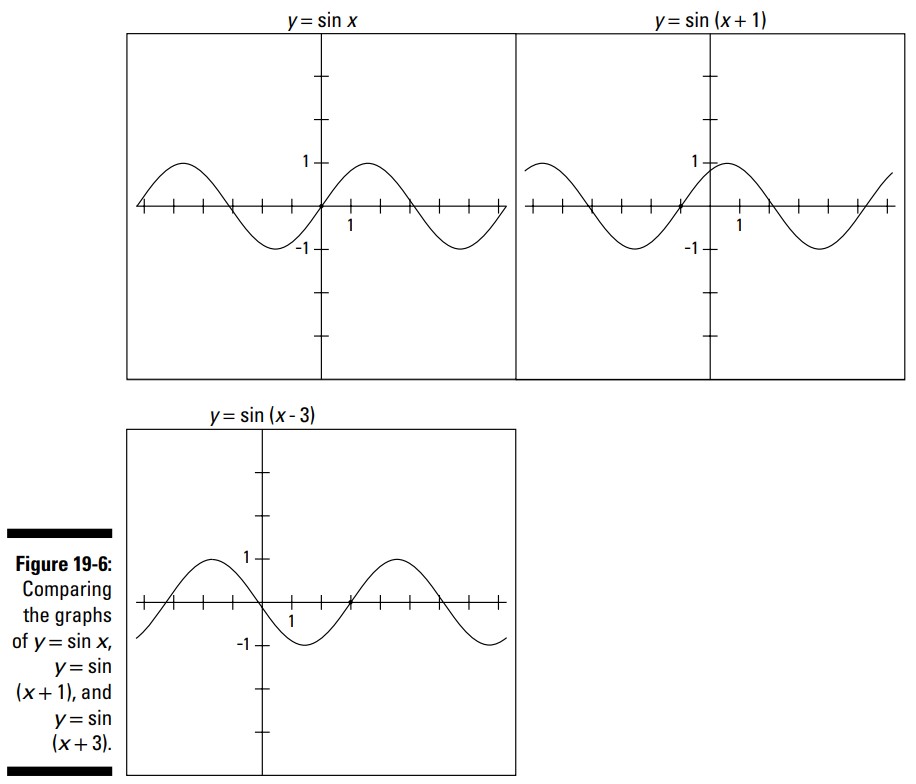
با افزودن یا تفریق یک عدد از زاویه در معادلۀ یک سینوس، شما می توانید آن منحنی را از موقعیت معمول آن، به سمت چپ یا راست منتقل کنید. این کار با بخش \(C\) از معادلۀ عمومی سینوس صورت می پذیرد. این انتقال منحنی سینوس را به منحنی کسینوس مرتبط می کند. اما خود انتقال سینوس حائز اهمیت می باشد: انتقال این منحنی به سمت چپ یا راست می تواند مکان هایی که آن منحنی از محور \(x\) یا هر خط افقی دیگر عبور می کند را تغییر دهد. به عنوان مثال، نمودار \(y=\sin (x+1)\) منحنی معمول سینوس است که \(1\) واحد به سمت چپ، سُر خورده است، و نمودار \(y=\sin(x-3)\) معادل \(3\) واحد به سمت راست، لغزیده است. شکل 6-19 نمودار اصلی سینوس و این دو معادلۀ منتقل شده را نشان می دهد.
در شکل 6-19 به نقطه ای که در هر نمودار مشخص شده است، نگاهی بیندازید. این نقطه نشان می دهد، هنگامی که عددی را به متغیر زاویه می افزایید یا از آن تفریق می کنید، چگونه یک تقاطع در نمودار منتقل می شود.


شکل 1-19 دو چرخۀ کامل از منحنی سینوس را نشان می دهد ـــ این منحنی روند خودش را دوبار در این نمودار نشان می دهد. اگر بتوانید منحنی این سینوس را تا ابد در هر دو جهت ببینید، هیچ تفاوتی نخواهد داشت. این منحنی الگوی یکسانی را بارها و بارها تا بی نهایت و ورای آن، تکرار می کند.
توصیف دامنۀ نوسان (amplitude) و دورۀ تناوب (period)
تابع سینوس و هر دگرگونی دیگرِ آن دارای دو ویژگی مهم می باشد: دامنۀ نوسان و دورۀ تناوبِ منحنیِ آن. شما می توانید با نگاه کردن به نمودار آن تابع یا معادلۀ آن، این ویژگیها را تعیین کنید.
بدست آوردن ارتفاع با دامنۀ نوسان
دامنۀ نوسانِ تابع سینوس برابر با فاصلۀ بین مقدار میانی یا خطی است که از وسط این نمودار تا بالاترین نقطۀ آن عبور می کند. به عبارت دیگر، دامنۀ نوسان برابر با نصف مسافت پایین ترین مقدار تا بالاترین مقدار می باشد. در معادلات سینوس و کسینوس، این دامنۀ نوسان برابر با ضریب سینوس یا کسینوس می باشد. به عنوان مثال، دامنۀ نوسان در معادلۀ \(y=\sin x \) برابر با \(1\) است. برای تغییر دادن دامنۀ نوسان، تابع سینوس را در عددی ضرب کنید. در شکل 2-19 نمودار \(y=3 \sin x\) و \(y=\frac{1}{2} = \sin x\) را می بینید.

همانطور که می بینید، ضرب کردن در عددی بزرگتر از \(1\) منجر می شود تا نمودار بالاتر و پایینتر برود. دامنۀ نوسان در \(y=3 \sin x \) برابر با \(3\) می باشد. برعکس، ضرب کردن در عددی کوچکتر از \(1\) (اما بزرگتر از \(0\)) منجر می شود مقدار نمودار کوچکتر شود ـــ از آنجا بالاتر یا پایینتر نرود. دامنۀ نوسان در \(y=\frac{1}{2} \sin x\) برابر با \(\frac{1}{2}\) می باشد.
نشان گذاری کردن با دورۀ تناوب
دورۀ تناوب (period) یک تابع میزان مقادیر ورودی است که منجر می شود آن تابع از تمامی مقادیر ممکن عبور کند و دوباره به نقطۀ آغازینی برسد تا این فرآیند را تکرار نماید. در مورد تابع سینوس، دورۀ تناوب برابر با \(2\pi\) یا \(360\) درجه می باشد. هر نقطه دلخواهی را بر روی منحنی سینوس انتخاب کنید، آن منحنی را به سمت راست یا چپ دنبال کنید، و در فاصلۀ \(2\pi\) یا \(360\) درجه، در امتداد محور \(x\)، از نقطه ای که آغاز کرده بودید، منحنی الگویش را دوباره تکرار می کند.
ضرب کردن متغیر زاویه، \(x\)، در یک عدد، دورۀ تناوب آن تابع را تغییر می دهد. اگر شما متغیر زاویه را در \(3\) ضرب کنید، مانند \(y=\sin 3x\)، سپس آن منحنی در مقدار فضای معمول، سه مرتبه تکمیل می شود. بنابراین، ضرب کردن در \(3\) در واقع طول دورۀ تناوب را کاهش می دهد. در مورد \(y=\sin \frac{1}{2}x\)، تنها نیمی از منحنی در همان فضا می گنجد. بنابراین، ضریبی کوچکتر از \(1\) مقدار ورودی هایی که آن تابع برای تکمیل یک چرخه نیاز دارد، افزایش می دهد. شکل 3-19 این دو نمودار نشان می دهد.
مکان ضریب یک تفاوت بزرگ را ایجاد می کند. ضرب کردن تابع سینوس در \(4\) و متغیر زاویۀ آن در \(4\) دو نمودار کاملاً متفاوت را منجر می شوند. نمودار \(y=4 \sin x\) بسیار بلندتر از حد معمول است ـــ دامنۀ نوسان آن بزرگتر از تابع استاندارد سینوس می باشد. نمودار \(y=\sin 4x\) دارای دامنۀ نوسان \(1\) می باشد، اما دورۀ تناوب آن کوچکتر است و منحنی آن در هم فشرده تر است ـــ سریعتر تکرار می شود.

رسمیت بخشیدن به معادلۀ سینوس
یک معادلۀ عمومی برای تابع سینوس برابر با \(y=A \sin B(x+C)+D\) می باشد. \(A\) و \(B\) اعدادی هستند که به ترتیب بر روی دامنۀ نوسان و دورۀ تناوبِ تابع اصلی سینوس تاثیر می گذارند. \(C\) و \(D\) در مکان های آغازین و پایانی جایجایی ایجاد می کنند و حتی می توانند منجر شوند این منحنی محور \(x\) را ترک کند. (در ادامۀ همین فصل در این مورد بیشتر بحث خواهیم کرد.) هنگامی که \(C\) و \(D\) هر دو برابر با صفر باشند، شما تابع اصلی سینوس را خواهید داشت: \(y=A \sin Bx\) .
نموار تابع \(y=A \sin Bx\) دارای دامنۀ نوسان \(A\) و دورۀ تناوب \(\frac{2\pi}{B}\) می باشد. دامنۀ نوسان، \(A\)، برابر با مسافت اندازه گیری شده از مقدار \(y\) از یک خط افقی که از میان این نمودار (یا مقدار میانگین) عبور می کند تا مقدار \(y\) در بالاترین نقطۀ منحنی سینوس می باشد، و \(B\) تعداد دفعاتی است که منحنی سینوس خودش را درون \(2\pi\) یا \(360\) درجه، تکرار می کند.
با حفظ کردن این دو مقدار، می توانید به سرعت نمودار منحنی اصلی سینوس را ترسیم کنید ـــ یا آن را در ذهنتان تجسم کنید. به عنوان مثال، هنگام ترسیم نمودار \(y=4 \sin 2x\) :
-
نمودار را با دامنۀ نوسان سازگار کنید.
دامنۀ نوسان برابر با \(4\) می باشد، بنابراین این نمودار از وسط \(4\) واحد به سمت بالا و \(4\) واحد به سمت پایین گسترش می یابد. برای اینکه مقداری فضا در بالا و پایین نمودار داشته باشید، محور \(y\) را از \(-5\) تا \(5\) تنظیم کنید.
-
دورۀ تناوب را لحاظ کنید.
ضریب \(2\) روی \(x\) بدین معناست که دو نمودار کامل از سینوس در فضایی که معمولاً تنها یکی جای می گیرد، قرار دارد.
-
نموار این منحنی را از \(-2\pi\) تا \(2\pi\) ترسیم کنید (شکل 4-19 را ببینید).
شما می توانید ببینید که این نمودار از \(-4\) تا \(4\) می رود و چهار چرخۀ کامل در فضایی که تنها دو چرخه جای می گیرد، قرار خواهد گرفت.

انتقال (translations) سینوس
شما می توانید با دامنۀ نوسان و دورۀ تناوب منحنی سینوس بازی کنید و نتیجه اش تغییرات جالبی در منحنی اصلی خواهد بود. با این حال، آن منحنی هنوز هم قابل تشخیص خواهد بود. شما هنوز هم می توانید منحنی های نرمی را که با چرخش از یک خط میانی بالا و پایین می روند را ببینید. علاوه بر این تغییرات، شما دو گزینۀ دیگر برای تغییر منحنی سینوس دارید ـــ انتقال منحنی به سمت بالا، پایین، یا پهلوها. این تغییر مکان ها انتقال (translations) آن منحنی نامیده می شوند. (برای مشاهدۀ یک بحث اولیه در مورد انتقال توابع می توانید فصل 3 را مرور کنید.) و این انتقال ها در معادلۀ عمومی تر سینوس لحاظ شده اند: \(y=A \sin B(x+C)+D\) .
انتقال منحنی سینوس به سمت بالا یا پایین
شما می توانید به سادگی با افزودن یا تفریق یک عدد در معادلۀ منحنی یک سینوس، آن منحنی را به سمت بالا یا پایین منتقل کنید. به لحاظ این معادله، اگر \(D\) عددی مثبت باشد، شما آن منحنی را به آن میزان به بالا منتقل می کنید؛ اگر \(D\) عددی منفی باشد، منحنی به سمت پایین منتقل می گردد. به عنوان مثال، نمودار \(y=\sin x + 4\) کل منحنی را \(4\) واحد به سمت بالا منتقل می کند، و منحنی سینوس از خط \(y=4\) به سمت بالا و پایینش عبور می کند. از سوی دیگر، نمودار \(y=\sin x-1\) همه چیز را \(1\) واحد به سمت پایین منتقل می کند. شکل 5-19 این دو نمودار را به شما نشان می دهد.

همانطور که می توانید ببینید، شکل اصلی منحنی سینوس هنوز هم قابل تشخیص است ـــ صرفاً منحنی ها در صفحۀ مختصات به سمت بالا یا پایین منتقل شده اند.
انتقال منحنی سینوس به سمت چپ یا راست
با افزودن یا تفریق یک عدد از زاویه در معادلۀ یک سینوس، شما می توانید آن منحنی را از موقعیت معمول آن، به سمت چپ یا راست منتقل کنید. این کار با بخش \(C\) از معادلۀ عمومی سینوس صورت می پذیرد. این انتقال منحنی سینوس را به منحنی کسینوس مرتبط می کند. اما خود انتقال سینوس حائز اهمیت می باشد: انتقال این منحنی به سمت چپ یا راست می تواند مکان هایی که آن منحنی از محور \(x\) یا هر خط افقی دیگر عبور می کند را تغییر دهد. به عنوان مثال، نمودار \(y=\sin (x+1)\) منحنی معمول سینوس است که \(1\) واحد به سمت چپ، سُر خورده است، و نمودار \(y=\sin(x-3)\) معادل \(3\) واحد به سمت راست، لغزیده است. شکل 6-19 نمودار اصلی سینوس و این دو معادلۀ منتقل شده را نشان می دهد.
در شکل 6-19 به نقطه ای که در هر نمودار مشخص شده است، نگاهی بیندازید. این نقطه نشان می دهد، هنگامی که عددی را به متغیر زاویه می افزایید یا از آن تفریق می کنید، چگونه یک تقاطع در نمودار منتقل می شود.

به تفاوت بین افزودن یا تفریق یک عدد به تابع و افزودن یا تفریق یک عدد به اندازۀ زاویه، توجه کنید. همانطور که با مقایسۀ شکل 5-19 و شکل 6-19 می توانید ببینید، این عملیات ها به صورت متفاوتی بر روی منحنی سینوس تاثیر می گذارند.
-
\(y=\sin x+2\) : افزودن \(2\) به یک تابع، منحنیِ آن را \(2\) واحد بالا می برد.
-
\(y=\sin (x+2)\) : افزودن \(2\) به متغیر زاویه، منحنی آن را \(2\) واحد به سمت چپ منتقل می کند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (3 دیدگاه)
دیدگاه خود را ثبت کنید: