خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ترسیم نمودار تابع سکانت

تکنیکهایی که برای ترسیم منحنی سکانت استفاده می کنید، به موازات همان تکنیکهایی هستند که برای ترسیم نمودار کسکانت استفاده کردید. ابتدا، خطوط مجانب را با تعیین اینکه کسرمتقابل سکانت یعنی کسینوس، در کجاها برابر با \(0\) می باشد، مشخص سازید. سپس آن کسرمتقابل را ترسیم کنید، و می توانید نقاط برگشت و شکل کلی نمودار سکانت را تعیین کنید.

از آنجا که تابع سکانت برابر با \(1\) تقسیم بر تابع کسینوس می باشد، تابع سکانت در جاهایی که کسینوس برابر با \(0\) باشد، وجود نخواهد داشت، یا به زبان ریاضی تعریف نشده (undefined) خواهد بود. شما می توانید معادلات این خطوط مجانب را با قرار دادن \(y\) برابر با آن مقادیر که در آنها کسینوس برابر با \(0\) است، بنویسید. بنابراین این خطوط مجانب عبارت از مواردی همچون موارد زیر می باشند:
$$x=-\frac{7\pi}{2},x=-\frac{5\pi}{2},x=-\frac{3\pi}{2},x=-\frac{\pi}{2},x=\frac{\pi}{2},x=\frac{3\pi}{2},x=\frac{5\pi}{2},x=\frac{7\pi}{2}$$
روش دیگر برای بیان کردن تمامی این خطوط مجانب اینست که آن را به شکل \(x=\frac{(2n+1)\pi}{2}\) بنویسید، که در آن \(n\) عددی صحیح است.
استفاده از نمودار کسینوس برای ترسیم نمودار تابع سکانت، ساده ترین روش است. نمودار کسینوس را به نرمی یا به شکل یک منحنی نقطه چین ترسیم کنید ـــ همان گونه که خطوط مجانب را می کشید. بسیاری کارهای بیهوده در ارتباط با این نمودار وجود دارد، اما شما باید تمامی این چیزهای زائد را نادیده بگیرید و بر روی نموداری که می خواهید تمرکز کنید.
برای ترسیم نمودار تابع سکانت:
نمودار سکانت به چند روش، متفاوت از نمودار کسکانت می باشد، اما یکی از بدیهی ترین روش ها اینست که این نمودار در اطراف محور \(y\) متقارن (symmetric) می باشد. سکانت یک بازتاب آینه ای بر روی آن محور می باشد. شما می توانید از این ویژگی برای انجام چیز جذابی در مورد این نمودار استفاده کنید.
انتقال ها و ضرب های معمول (به فصل 3 مراجعه کنید) بر روی نمودار سکانت تاثیر می گذارند. اگر این تابع را در \(\frac{1}{6}\) ضرب کنید و \(2\pi\) را به متغیر زاویۀ آن بیفزایید، چنانکه در معادلۀ \(y=\frac{1}{6} \sec(x+2\pi)\) می بینید، شکل 10-21 آنچه را که رخ می دهد به شما نشان داده است.
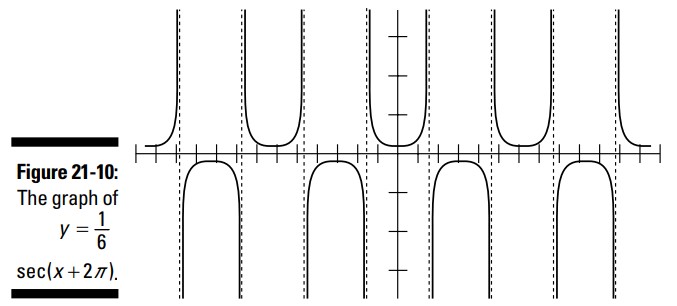
در مقایسه با \(y=\sec x\)، نمودار موجود در شکل 10-21 بسیار به محور \(x\) نزدیکتر است و به نظر می آید که بین خطوط مجانب مسطح شده است. این تغییرات زمانی رخ می دهند که آن تابع را در عددی بین \(0\) و \(1\) ضرب کنید. نقطۀ برگشت (turning point) هنوز در همان محل قبلی اش است، اما مقدار \(y\) بسیار به \(0\) نزدیکتر است.
چیز عجیب دیگر اینست که این خطوط مجانب متفاوت به نظر نمی رسند. آنها متفاوت نیستند ـــ و نباید متفاوت باشند. با افزودن \(2\pi\) به متغیر زاویه، این نمودار را \(2\pi\) واحد به سمت چپ منتقل می کنید. این نمودار در واقع به سمت چپ منتقل شده است، اما شما نمی توانید این انتقال را تشخیص دهید، زیرا نمودار جدید کاملاً بر روی نمودار قبلی افتاده است. هنگامی که انتقال برابر با دورۀ تناوب آن تابع باشد (دورۀ تناوب تابع طول بازه ای است که برای مقادیر تابع طول می کشد تا دوباره خودشان را تکرار کنند)، این تغییر آشکار نخواهد بود.

تعیین خطوط مجانب
از آنجا که تابع سکانت برابر با \(1\) تقسیم بر تابع کسینوس می باشد، تابع سکانت در جاهایی که کسینوس برابر با \(0\) باشد، وجود نخواهد داشت، یا به زبان ریاضی تعریف نشده (undefined) خواهد بود. شما می توانید معادلات این خطوط مجانب را با قرار دادن \(y\) برابر با آن مقادیر که در آنها کسینوس برابر با \(0\) است، بنویسید. بنابراین این خطوط مجانب عبارت از مواردی همچون موارد زیر می باشند:
$$x=-\frac{7\pi}{2},x=-\frac{5\pi}{2},x=-\frac{3\pi}{2},x=-\frac{\pi}{2},x=\frac{\pi}{2},x=\frac{3\pi}{2},x=\frac{5\pi}{2},x=\frac{7\pi}{2}$$
روش دیگر برای بیان کردن تمامی این خطوط مجانب اینست که آن را به شکل \(x=\frac{(2n+1)\pi}{2}\) بنویسید، که در آن \(n\) عددی صحیح است.
ترسیم نمودار سکانت
استفاده از نمودار کسینوس برای ترسیم نمودار تابع سکانت، ساده ترین روش است. نمودار کسینوس را به نرمی یا به شکل یک منحنی نقطه چین ترسیم کنید ـــ همان گونه که خطوط مجانب را می کشید. بسیاری کارهای بیهوده در ارتباط با این نمودار وجود دارد، اما شما باید تمامی این چیزهای زائد را نادیده بگیرید و بر روی نموداری که می خواهید تمرکز کنید.
برای ترسیم نمودار تابع سکانت:
-
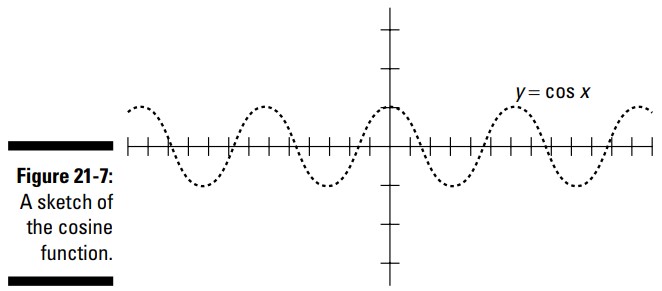
همانطور که در شکل 7-21 می بینید، نمودار \(y=\cos x\) را از \(-4\pi\) تا \(4\pi\) ترسیم کنید.
-
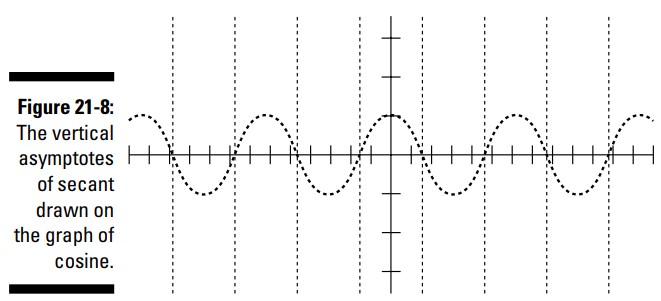
همانطور که شکل 8-21 نشان می دهد، خطوط مجانب عمودی را از میان طول از مبدأها (جایی که این منحنی از محور \(x\) عبور می کند) ترسیم کنید.
-
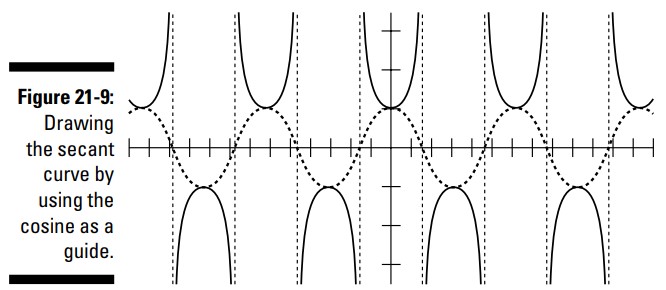
همانطور که در شکل 9-21 می بینید، نمودار \(y=\sec x\) را بین این خطوط مجانب و در بالا و پایین منحنی کسینوس، ترسیم کنید.
سکانت از بالای منحنی کسینوس رو به بالا و از پایین منحنی کسینوس رو به پایین می رود ـــ به ترتیب در محلهایی که کسینوس دارای مقدار \(1\) و \(-1\) می باشد.
کار کردن در اطراف سکانت
نمودار سکانت به چند روش، متفاوت از نمودار کسکانت می باشد، اما یکی از بدیهی ترین روش ها اینست که این نمودار در اطراف محور \(y\) متقارن (symmetric) می باشد. سکانت یک بازتاب آینه ای بر روی آن محور می باشد. شما می توانید از این ویژگی برای انجام چیز جذابی در مورد این نمودار استفاده کنید.
انتقال ها و ضرب های معمول (به فصل 3 مراجعه کنید) بر روی نمودار سکانت تاثیر می گذارند. اگر این تابع را در \(\frac{1}{6}\) ضرب کنید و \(2\pi\) را به متغیر زاویۀ آن بیفزایید، چنانکه در معادلۀ \(y=\frac{1}{6} \sec(x+2\pi)\) می بینید، شکل 10-21 آنچه را که رخ می دهد به شما نشان داده است.

در مقایسه با \(y=\sec x\)، نمودار موجود در شکل 10-21 بسیار به محور \(x\) نزدیکتر است و به نظر می آید که بین خطوط مجانب مسطح شده است. این تغییرات زمانی رخ می دهند که آن تابع را در عددی بین \(0\) و \(1\) ضرب کنید. نقطۀ برگشت (turning point) هنوز در همان محل قبلی اش است، اما مقدار \(y\) بسیار به \(0\) نزدیکتر است.
چیز عجیب دیگر اینست که این خطوط مجانب متفاوت به نظر نمی رسند. آنها متفاوت نیستند ـــ و نباید متفاوت باشند. با افزودن \(2\pi\) به متغیر زاویه، این نمودار را \(2\pi\) واحد به سمت چپ منتقل می کنید. این نمودار در واقع به سمت چپ منتقل شده است، اما شما نمی توانید این انتقال را تشخیص دهید، زیرا نمودار جدید کاملاً بر روی نمودار قبلی افتاده است. هنگامی که انتقال برابر با دورۀ تناوب آن تابع باشد (دورۀ تناوب تابع طول بازه ای است که برای مقادیر تابع طول می کشد تا دوباره خودشان را تکرار کنند)، این تغییر آشکار نخواهد بود.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: