خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ترسیم نمودار توابع معکوس مثلثاتی

شش تابع مثلثاتی اصلی همگی دارای معکوس می باشند. در فصل 15 اطلاعاتی در مورد نمادهای استفاده شده برای نشان دادن توابع معکوس، اینکه دامنه های مربوط به آنها چه می باشند، و اینکه چگونه از آنها استفاده کنید، ارائه شده است.

توابع معکوس مثلثاتی به شرح زیر می باشند:
$$y=\sin^{-1}x,y=\cos^{-1}x,y=\tan^{-1}x,y=\cot^{-1}x,y=sec^{-1}x,y=\csc^{-1}x$$
توابع معکوس مثلثاتی برای حل کردن معادلات مثلثاتی یا انجام کاربردهای شامل مثلثات سودمند هستند. نمودارهای توابع معکوس مثلثاتی نسبتاً منحصر به فرد می باشند؛ سینوس معکوس و کسینوس معکوس نسبتاً غیرمنتظره و بی ارتباط با یکدیگرند، اما تانژانت معکوس و کتانژانت معکوس، به نظر می رسند که با محدوده ای باریک، تا ابد ادامه می یابند. دلیل اینکه این تفاوت بزرگ وجود دارد، بُرد یا خروجی های توابع اصلی آنها می باشد. برد سینوس و کسینوس بین \(-1\) و \(1\) می باشد، بنابراین توابع معکوس آنها صرفاً ورودی هایی از آن مقادیر خواهند داشت. تانژانت و کتانژانت دارای برد بی نهایتی می باشند، به همین دلیل هم هست که معکوس آنها دارای دامنۀ بی نهایتی می باشد.
اساساً چرا باید نمودارهای توابع معکوس اهمیتی داشته باشند؟ به همان دلیلی که تمامی تصاویر دیگر حائز اهمیتند ـــ بخاطر تاثیر بصری آنها. به ویژه در دنیای توابع مثلثاتی، به خاطر آوردن شکل کلی نمودار یک تابع، کمک بسیاری در بیادآوری اطلاعات بیشتری در مورد مقادیر آن تابع و استفادۀ موثرتر از آنها می کند.
قبل از اینکه در این بخش شیرجه بزنید، ممکن است بخواهید به فصل 3 بازگردید و موضوعاتی در مورد توابع معکوس همچون دامنه و برد آنها و مقادیر متناظرشان، را مرور نمایید.
دو نمودار اول به نوعی با یکدیگر مرتبطند ـــ دارای ویژگیهای مشترکی می باشند. مقادیر ورودی برای هر دو تابع \(y=\sin^{-1}x\) و \(y=\cos^{-1}x\) شامل تمامی اعداد بین \(-1\) و \(1\)، و خود این دو عدد، می باشند. دلیل اینکه ورودی ها محدود به این اعداد می باشند اینست که آنها خروجی توابع سینوس و کسینوس می باشند.
مقادیر خروجی، یا بُرد، این دو تابع معکوس، متفاوت می باشند. برد \(y=\sin^{-1}x\) عبارت از زوایای اولین و چهارمین ربع صفحه می باشند. در واحد رادیان، این برد از \(-\frac{\pi}{2}\) تا \(\frac{\pi}{2}\) می باشند؛ به مقادیر برآوردی اعشاری، این برد از \(-1.571\) تا \(1.571\) می باشد. از سوی دیگر، برد \(y=\cos^{-1}x\)، عبارت از زوایای موجود در اولین و دومین ربع صفحه، یا زوایای بین \(0\) تا \(\pi\) می باشند. به مقادیر برآوردی اعشاری این برد از \(0\) تا \(3.142\) می باشد.
شکل 11-21 به شما نشان می دهد که نمودار سینوس معکوس و کسینوس معکوس، به چه شکلی می باشند.
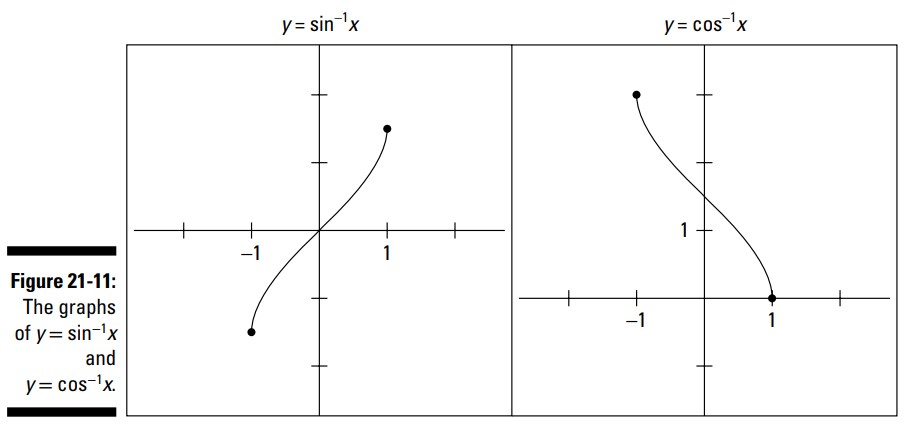
نقاطی که بر روی این نمودار نشان داده شده اند عبارت از \(x=-1\) و \(x=1\) می باشند. این نقاط بیشینه ترین مقادیر ورودی می باشند. مقادیر \(y\) نشان دهندۀ اندازه های زاویه می باشند. اگر می خواهید نقطه ای را بر روی هر کدام از این نمودارها بیابید، صرفاً اعداد خاصی بین \(-1\) و \(1\) را بیابید، و نقاط متناظر با آن مقادیر \(x\) را بر روی نمودار پیدا کنید.
توابع تانژانت و کتانژانت دارای ورودیهای محدودی می باشند ـــ برخی از زوایا با آنها مطابقت ندارند. اما خروجی های آنها از تمامی اعداد حقیقی استفاده می کنند. اگر این دو گروه از اعداد را با یکدیگر تعویض کنید تا درخور تانژانت معکوس و کتانژانت معکوس گردند، می توانید بگویید که ورودی ها از تمامی اعداد حقیقی استفاده می کنند و خروجی ها محدود می باشند. نمودار این دو تابع معکوس کاملاً جذاب می باشد زیرا هر دوی آنها شامل دو خط مجانب افقی می باشند. این خطوط مجانب به شکل منحنی ها کمک می کند و روی این حقیقت تاکید می کند که برخی زوایا با این توابع کار نمی کنند.
دو خط مجانب افقی برای تابع تانژانت معکوس عبارت از \(y=-\frac{\pi}{2}\) و \(y=\frac{\pi}{2}\) می باشند، زیرا تابع تانژانت برای این دو اندازۀ زاویه وجود ندارد. هر جایی که تابع کسینوس برابر با \(0\) باشد، تابع تانژانت در آنجا تعریف نشده است. اگر نیاز به مرور و یادآوری در مورد تابع تانژانت دارید، به فصل های 7 و 8 مراجعه کنید. نمودار تابع تانژانت معکوس دارای مقادیر \(x\) از منفی بی نهایت تا مثبت بی نهایت می باشد، همراه با تمامی مقادیر \(y\) که بین آن دو خط مجانب قرار گرفته اند.
دو خط مجانب افقی برای تابع کتانژانت معکوس عبارت از \(y=0\) و \(y=\pi\) می باشند. همانند تانژانت معکوس، تابع کتانژانت معکوس بین این خطوط مجانب از منفی بی نهایت تا مثبت بی نهایت می رود. هر دوی این نمودارها را در شکل 12-21 بررسی کنید.
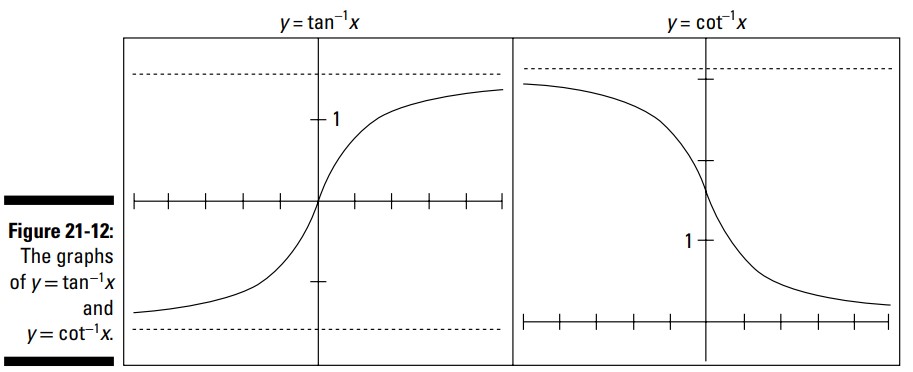
مهمترین تفاوت بین این دو نمودار در اینست که منحنی تانژانت معکوس از چپ به راست بالا می رود و منحنی کتانژانت معکوس از چپ به راست سقوط می کند. همچنین، خطوط مجانب افقی برای تانژانت معکوس اندازۀ زوایایی را می گیرند که در اولین و چهارمین ربع صفحه باشند؛ خطوط مجانب افقی برای کتانژانت معکوس ربع صفحۀ اول و دوم را می گیرند. مسلماً، اندازه های بین این دو خط مجانب، با برد این دو تابع معکوس سازگارند.
نمودارهای سکانت معکوس و کسکانت معکوس نیاز به اندکی توضیح دارند. قبل از هر چیز، یادتان باشد که توابع سکانت و کسکانت بین \(-1\) و \(1\) هیچ مقدار خروجی یا مقدار \(y\) ندارند، بنابراین یک فضای کاملاً باز در وسط نمودارهای آنها قرار می گیرد. یعنی یک فضای باز بین مقادیر \(x\) از \(-1\) تا \(1\) در نمودار معکوس هایشان ایجاد می شود. با این وجود، نمودارهای سکانت و کسکانت در امتداد محور \(y\) بی نهایت بالا و بی نهایت پایین می روند. بنابراین، نمودار معکوس های آنها دارای یک خط مجانب افقی می باشد. شکل 13-21 این نمودارها را نشان می دهد.
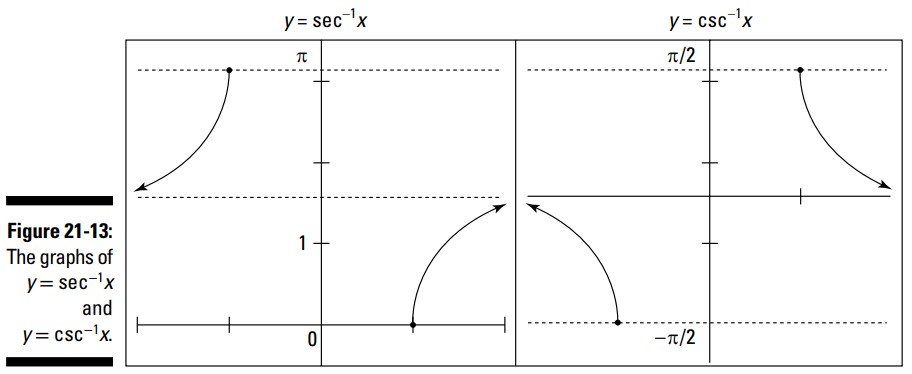
نمودار \(y=\sec^{-1} x\) بین \(0\) و \(\pi\) بر روی محور \(y\) قرار می گیرد. تمامی مقادیر خروجی آنها در اولین و دومین ربع صفحه قرار می گیرند. اما یک خط مجانب افقی از وسط این نمودار عبور می کند: خط \(y=\frac{\pi}{2}\) . سکانت در \(\frac{\pi}{2}\) تعریف نشده است، بنابراین معکوس آن در آنجا دارای مقادیر خروجی نمی باشد. نمودار سکانت معکوس از نقطۀ \((1,0)\) آغاز می شود و به سمت بالا می رود، در زیر خط مجانب افقی قرار می گیرد به نحویکه مقادیر \(x\) آن تا مثبت بی نهایت پیش می رود. همچنین از منفی بی نهایت در امتداد محور \(x\) در بالای خط مجانب افقی، رو به سمت بالا تا نقطۀ \((-1,\pi)\) پیش می رود.
نمودار \(y=\csc^{-1}x\)، همراه با خط مجانب افقیِ \(y=0\)، بین \(-\frac{\pi}{2}\) و \(\frac{\pi}{2}\) قرار می گیرد. (کسکانت در \(x=0\) تعریف نشده است، بنابراین معکوس آن در آنجا خروجی ندارد.) نمودار کسکانت معکوس اندازۀ زوایایی از اولین و چهارمین ربع صفحه را پوشش می دهد. در سمت راست، این نمودار از نقطۀ \(\biggl(1,\frac{\pi}{2}\biggr)\) آغاز می شود و رو به پایین به سوی خط مجانب افقی به شکلی که مقادیر \(x\) آن تا مثبت بی نهایت پیش می رود. در سمت چپ، مقادیر \(x\) این نمودار از منفی بی نهایت می آیند، جایی که فقط زیر خط مجانب هستند، و رو به سمت پایین تا نقطۀ \(\biggl(-1,-\frac{\pi}{2}\biggr)\) می روند.

توابع معکوس مثلثاتی به شرح زیر می باشند:
$$y=\sin^{-1}x,y=\cos^{-1}x,y=\tan^{-1}x,y=\cot^{-1}x,y=sec^{-1}x,y=\csc^{-1}x$$
توابع معکوس مثلثاتی برای حل کردن معادلات مثلثاتی یا انجام کاربردهای شامل مثلثات سودمند هستند. نمودارهای توابع معکوس مثلثاتی نسبتاً منحصر به فرد می باشند؛ سینوس معکوس و کسینوس معکوس نسبتاً غیرمنتظره و بی ارتباط با یکدیگرند، اما تانژانت معکوس و کتانژانت معکوس، به نظر می رسند که با محدوده ای باریک، تا ابد ادامه می یابند. دلیل اینکه این تفاوت بزرگ وجود دارد، بُرد یا خروجی های توابع اصلی آنها می باشد. برد سینوس و کسینوس بین \(-1\) و \(1\) می باشد، بنابراین توابع معکوس آنها صرفاً ورودی هایی از آن مقادیر خواهند داشت. تانژانت و کتانژانت دارای برد بی نهایتی می باشند، به همین دلیل هم هست که معکوس آنها دارای دامنۀ بی نهایتی می باشد.
اساساً چرا باید نمودارهای توابع معکوس اهمیتی داشته باشند؟ به همان دلیلی که تمامی تصاویر دیگر حائز اهمیتند ـــ بخاطر تاثیر بصری آنها. به ویژه در دنیای توابع مثلثاتی، به خاطر آوردن شکل کلی نمودار یک تابع، کمک بسیاری در بیادآوری اطلاعات بیشتری در مورد مقادیر آن تابع و استفادۀ موثرتر از آنها می کند.
قبل از اینکه در این بخش شیرجه بزنید، ممکن است بخواهید به فصل 3 بازگردید و موضوعاتی در مورد توابع معکوس همچون دامنه و برد آنها و مقادیر متناظرشان، را مرور نمایید.
ترسیم نمودار سینوس معکوس و کسینوس معکوس
دو نمودار اول به نوعی با یکدیگر مرتبطند ـــ دارای ویژگیهای مشترکی می باشند. مقادیر ورودی برای هر دو تابع \(y=\sin^{-1}x\) و \(y=\cos^{-1}x\) شامل تمامی اعداد بین \(-1\) و \(1\)، و خود این دو عدد، می باشند. دلیل اینکه ورودی ها محدود به این اعداد می باشند اینست که آنها خروجی توابع سینوس و کسینوس می باشند.
مقادیر خروجی، یا بُرد، این دو تابع معکوس، متفاوت می باشند. برد \(y=\sin^{-1}x\) عبارت از زوایای اولین و چهارمین ربع صفحه می باشند. در واحد رادیان، این برد از \(-\frac{\pi}{2}\) تا \(\frac{\pi}{2}\) می باشند؛ به مقادیر برآوردی اعشاری، این برد از \(-1.571\) تا \(1.571\) می باشد. از سوی دیگر، برد \(y=\cos^{-1}x\)، عبارت از زوایای موجود در اولین و دومین ربع صفحه، یا زوایای بین \(0\) تا \(\pi\) می باشند. به مقادیر برآوردی اعشاری این برد از \(0\) تا \(3.142\) می باشد.
شکل 11-21 به شما نشان می دهد که نمودار سینوس معکوس و کسینوس معکوس، به چه شکلی می باشند.

نقاطی که بر روی این نمودار نشان داده شده اند عبارت از \(x=-1\) و \(x=1\) می باشند. این نقاط بیشینه ترین مقادیر ورودی می باشند. مقادیر \(y\) نشان دهندۀ اندازه های زاویه می باشند. اگر می خواهید نقطه ای را بر روی هر کدام از این نمودارها بیابید، صرفاً اعداد خاصی بین \(-1\) و \(1\) را بیابید، و نقاط متناظر با آن مقادیر \(x\) را بر روی نمودار پیدا کنید.
ترسیم نمودار تانژانت معکوس و کتانژانت معکوس
توابع تانژانت و کتانژانت دارای ورودیهای محدودی می باشند ـــ برخی از زوایا با آنها مطابقت ندارند. اما خروجی های آنها از تمامی اعداد حقیقی استفاده می کنند. اگر این دو گروه از اعداد را با یکدیگر تعویض کنید تا درخور تانژانت معکوس و کتانژانت معکوس گردند، می توانید بگویید که ورودی ها از تمامی اعداد حقیقی استفاده می کنند و خروجی ها محدود می باشند. نمودار این دو تابع معکوس کاملاً جذاب می باشد زیرا هر دوی آنها شامل دو خط مجانب افقی می باشند. این خطوط مجانب به شکل منحنی ها کمک می کند و روی این حقیقت تاکید می کند که برخی زوایا با این توابع کار نمی کنند.
دو خط مجانب افقی برای تابع تانژانت معکوس عبارت از \(y=-\frac{\pi}{2}\) و \(y=\frac{\pi}{2}\) می باشند، زیرا تابع تانژانت برای این دو اندازۀ زاویه وجود ندارد. هر جایی که تابع کسینوس برابر با \(0\) باشد، تابع تانژانت در آنجا تعریف نشده است. اگر نیاز به مرور و یادآوری در مورد تابع تانژانت دارید، به فصل های 7 و 8 مراجعه کنید. نمودار تابع تانژانت معکوس دارای مقادیر \(x\) از منفی بی نهایت تا مثبت بی نهایت می باشد، همراه با تمامی مقادیر \(y\) که بین آن دو خط مجانب قرار گرفته اند.
دو خط مجانب افقی برای تابع کتانژانت معکوس عبارت از \(y=0\) و \(y=\pi\) می باشند. همانند تانژانت معکوس، تابع کتانژانت معکوس بین این خطوط مجانب از منفی بی نهایت تا مثبت بی نهایت می رود. هر دوی این نمودارها را در شکل 12-21 بررسی کنید.

مهمترین تفاوت بین این دو نمودار در اینست که منحنی تانژانت معکوس از چپ به راست بالا می رود و منحنی کتانژانت معکوس از چپ به راست سقوط می کند. همچنین، خطوط مجانب افقی برای تانژانت معکوس اندازۀ زوایایی را می گیرند که در اولین و چهارمین ربع صفحه باشند؛ خطوط مجانب افقی برای کتانژانت معکوس ربع صفحۀ اول و دوم را می گیرند. مسلماً، اندازه های بین این دو خط مجانب، با برد این دو تابع معکوس سازگارند.
ترسیم نمودار سکانت معکوس و کسکانت معکوس
نمودارهای سکانت معکوس و کسکانت معکوس نیاز به اندکی توضیح دارند. قبل از هر چیز، یادتان باشد که توابع سکانت و کسکانت بین \(-1\) و \(1\) هیچ مقدار خروجی یا مقدار \(y\) ندارند، بنابراین یک فضای کاملاً باز در وسط نمودارهای آنها قرار می گیرد. یعنی یک فضای باز بین مقادیر \(x\) از \(-1\) تا \(1\) در نمودار معکوس هایشان ایجاد می شود. با این وجود، نمودارهای سکانت و کسکانت در امتداد محور \(y\) بی نهایت بالا و بی نهایت پایین می روند. بنابراین، نمودار معکوس های آنها دارای یک خط مجانب افقی می باشد. شکل 13-21 این نمودارها را نشان می دهد.

نمودار \(y=\sec^{-1} x\) بین \(0\) و \(\pi\) بر روی محور \(y\) قرار می گیرد. تمامی مقادیر خروجی آنها در اولین و دومین ربع صفحه قرار می گیرند. اما یک خط مجانب افقی از وسط این نمودار عبور می کند: خط \(y=\frac{\pi}{2}\) . سکانت در \(\frac{\pi}{2}\) تعریف نشده است، بنابراین معکوس آن در آنجا دارای مقادیر خروجی نمی باشد. نمودار سکانت معکوس از نقطۀ \((1,0)\) آغاز می شود و به سمت بالا می رود، در زیر خط مجانب افقی قرار می گیرد به نحویکه مقادیر \(x\) آن تا مثبت بی نهایت پیش می رود. همچنین از منفی بی نهایت در امتداد محور \(x\) در بالای خط مجانب افقی، رو به سمت بالا تا نقطۀ \((-1,\pi)\) پیش می رود.
نمودار \(y=\csc^{-1}x\)، همراه با خط مجانب افقیِ \(y=0\)، بین \(-\frac{\pi}{2}\) و \(\frac{\pi}{2}\) قرار می گیرد. (کسکانت در \(x=0\) تعریف نشده است، بنابراین معکوس آن در آنجا خروجی ندارد.) نمودار کسکانت معکوس اندازۀ زوایایی از اولین و چهارمین ربع صفحه را پوشش می دهد. در سمت راست، این نمودار از نقطۀ \(\biggl(1,\frac{\pi}{2}\biggr)\) آغاز می شود و رو به پایین به سوی خط مجانب افقی به شکلی که مقادیر \(x\) آن تا مثبت بی نهایت پیش می رود. در سمت چپ، مقادیر \(x\) این نمودار از منفی بی نهایت می آیند، جایی که فقط زیر خط مجانب هستند، و رو به سمت پایین تا نقطۀ \(\biggl(-1,-\frac{\pi}{2}\biggr)\) می روند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: