اکنون زمان آن فرا رسیده است که تمامی دانشتان را به کار بگیرید و چندین مسالۀ جدی ترسیم نمودار را انجام دهید. در معادلۀ عمومیِ یک تابع مثلثاتی، \(y=Af[B(x+C)]+D\)، حروف \(A\)، \(B\)، \(C\)، و \(D\) همگی نشان دهندۀ مقادیری می باشند، اما آنها باید دقیقاً در همان محل های خاص خودشان باشند، و معادله باید دقیقاً در همین شکل باشد. اگر می خواهید از این مقادیر برای فهمیدن اینکه شکل نمودار باید چگونه باشد، استفاده کنید، نیاز دارید تا با فاکتورگیری، ضرب کردن، یا دستکاری معادله به سایر روشها، آن را به این شکل عمومی در بیاورید.





احتمال زیادی وجود دارد که شما نمودارهای این بخش را با کمک یک ماشین حساب نموداری ترسیم کنید. تنها مشکل با ماشین حسابهای نموداری اینست که وارد کردن این توابع پیچیده به درستی معمولاً یک چالش واقعی است. شما نمی توانید از کروشه ها یا آکولادها برای واضح نگهداشتن این گروه بندیها استفاده کنید. اگر هم بخواهید با پرانتزهای زیادی کار کنید، نوشته هایتان شلوغ می شود و ممکن است گیر کنید. مهمترین دلیلی که این مثالها را در این بخش آورده ام اینست که بدانید باید انتظار چه چیزی را داشته باشید. هنگامی که بدانید چگونه تمامی این دگرگونی ها کار می کنند، قادر خواهید بود تا اگر خطایی در ماشین حساب نموداریتان داشته باشید آن را شناسایی کنید.

اولین مثال شامل ترسیم نمودار \(y=3 \sin [2(x-\frac{\pi}{4})]+1\) می باشد.

1. دامنۀ نوسان (amplitude) این منحنی را تعیین کنید.
   \(3\) نشان دهندۀ \(A\)، که دامنۀ نوسان این منحنی سینوس است، می باشد. این تابع به اندازۀ \(3\) واحد در بالا و پایین مرکز، کِش می آید. \(3\) مثبت است، بنابراین این منحنی بر روی یک خط افقی برنمی گردد یا بازتابیده نمی شود.
   
   
2. دورۀ تناوب (period) این تابع را بیابید.
   \(2\) نشان دهندۀ \(B\) می باشد، و بدین معناست که این منحنی دو چرخۀ کامل را در فضایی که معمولاً فقط یک چرخه کامل وجود دارد، خواهد داشت. از آنجا که دورۀ تناوب عادی تابع سینوس برابر با \(2\pi\) واحد می باشد، در این تابع دورۀ تناوب برابر با \(\frac{2\pi}{2}\) یا \(\pi\) واحد می باشد.
   
   
3. انتقال به چپ یا راست را تعیین کنید.
   \(-\frac{\pi}{4}\) نشان دهندۀ مقدار \(C\) می باشد. از آنجا که \(C\) منفی می باشد، این انتقال برابر با \(\frac{\pi}{4}\) واحد به سمت راست می باشد.
   
   
4. انتقال به بالا یا پایین را بیابید.
   آخرین عدد، یعنی \(1\)، مقدار \(D\) می باشد، که نشان دهندۀ انتقال به بالا برابر با \(1\) واحد می باشد.
   
   
5. تمامی این مقادیر را وارد کنید تا نمودار این معادله را ترسیم کنید، شکل 2-22 این نمودار را نشان می دهد.
   

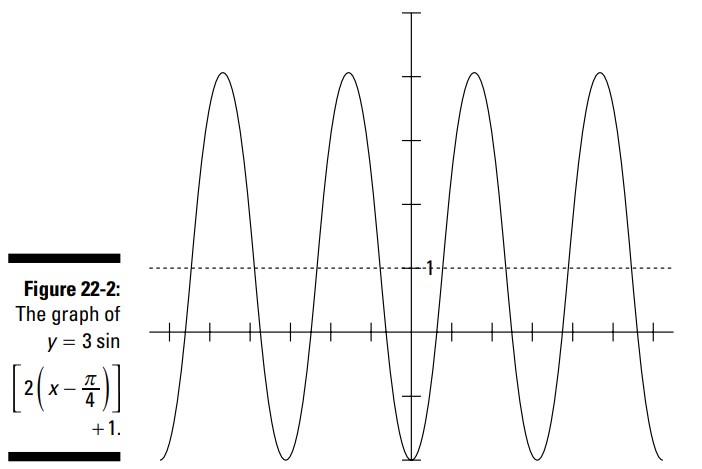
در شکل 2-22، من خط \(y=1\) را برای نشان دادن میانه ترسیم کرده ام، تا شما بتوانید نتیجۀ انتقال عمودی را ببینید. این نمودار از \(-2\pi\) تا \(2\pi\) بر روی محور \(x\) نشان داده شده است، که در حالت عادی انتظار یافتن دو چرخۀ کامل را در آن دارید. در عوض، این نمودار چهار چرخۀ کامل دارد.

نمودار بعدی یک برگردان بر روی یک خط افقی دارد. این منحنی روی محور \(x\) برنمی گردد زیرا به اندازۀ \(3\) واحد پایین رفته است. در عوض، این چرخش بر روی خط افقی \(y=-3\) صورت پذیرفته است. بدون معطلی، در اینجا چگونگی ترسیم نمودار \(y=-2\cos[\frac{1}{3}(x+\pi)]-3\) را داریم.

1. دامنۀ نوسان را تعیین کنید.
   \(-2\) در ابتدای این معادله دو چیز را به شما می گوید. اول اینکه، دامنۀ نوسان برابر با \(2\) می باشد، یا این منحنی دو برابر حد معمول ارتفاع دارد. این علامت منفی به شما می گوید که کل منحنی کسینوس بر روی یک خط افقی برگردانده شده است. جایی که این منحنی در حالت معمول بالا می رود، در اینجا پایین می رود، و برعکس.
   
   
2. دورۀ تناوب را بیابید.
   ضریب \(\frac{1}{3}\) این منحنی را به میزان قابل توجهی گسترش داده است ـــ تنها یک سوم از این منحنی در همان فضایی که معمولاً یک دورۀ تناوب \(2\pi\) دارد، جای گرفته است ـــ دورۀ تناوب تابع کسینوس \(2\pi\) است. در واقع، دورۀ تناوب جدید، برابر است با:
   $$2\pi \div \frac{1}{3} = 2\pi \cdot 3 = 6\pi$$
   
3. انتقال به سمت چپ یا راست را تعیین کنید.
   مقدار \(C\) برابر با \(\pi\) می باشد، که اندکی از \(3\) واحد بیشتر است. از آنجا که \(C\) مثبت است، این نمودار \(3\) واحد به سمت چپ منتقل می شود.
   
   
4. انتقال عمودی را بیابید.
   \(D\) نشان دهندۀ عدد \(-3\) می باشد، بنابراین کل این نمودار \(3\) واحد به سمت پایین منتقل می شود.
   
   
5. اکنون تمامی این مقادیر را مورد استفاده قرار دهید تا این منحنی را از \(-2\pi\) تا \(2\pi\) ترسیم کنید، شکل 3-22 را ببینید.
   

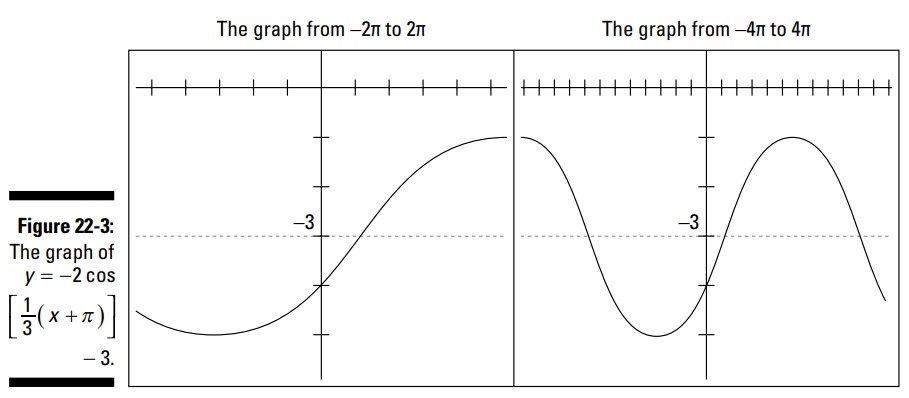
همانطور که از روی شکل 3-22 می توانید ببینید، صرفاً ترسیم نمودار از \(-2\pi\) تا \(2\pi\) یک چرخۀ کامل را نشان نمی دهد. این دورۀ تناوب برابر با \(6\pi\) می باشد، بنابراین این نمودار به فضای بیشتری نیاز دارد. این دو نمودار اندکی متفاوت به نظر می رسند ـــ نمودار سمت راست تندتر به نظر می رسد، زیرا مقیاس محور \(x\) آن متفاوت می باشد. هر دوی این نمودارها برای تابع یکسانی هستند. خط نقطه چین برابر با \(y=-3\) می باشد، که میانه یا میانگین این نمودار می باشد.

این نمودار آخر به شما نشان می دهد که شما همیشه مجبور نیستید که برای یکی از این حروف الفبا در شکل عمومی معادلۀ توابع مثلثاتی، مقداری را داشته باشید. خوب، در واقع، هر کدام از این حروف الفبا مقداری دارند، اما هنگامی که مقدار آن برابر با \(1\) یا \(0\) باشد، نشان داده نمی شود. کافیست این را بدانید، بخشی از این معادله که دارای مقدار \(1\) یا \(0\) باشد، نمودار اصلی را تغییر نمی دهد. در نمودار \(y=-\tan 2x+\pi\)، شما دو وضعیت را می یابید که نمودار اصلی را تغییر نمی دهند.

1. تندی را تعیین کنید.
   در تابع تانژانت، من به این ضریب به عنوان دامنۀ نوسان اشاره نمی کنم، زیرا منحنی تانژانت، همانند منحنی های سینوس و کسینوس، دارای یک نقطۀ بالاتر یا پایینتر نمی باشد. هر ضریبی به عنوان \(A\) بر روی تندی (شیب) اثر می گذارد. در این مورد، میزان تندی تغییری نمی کند، زیرا \(A\) در واقع برابر با \(1\) است. از آنجا که \(1\) منفی می باشد، این نمودار بر روی یک خط افقی برگردان می شود.
   
   
2. دورۀ تناوب این تابع را بیابید.
   ضریب \(2\) بر روی اندازۀ این زاویه، منجر می شود دورۀ تناوب این منحنی تانژانت برابر با \(\frac{\pi}{2}\) گردد، زیرا دورۀ تناوب معمولی تابع تانژانت \(\pi\) می باشد، و شما باید آن را تقسیم بر \(2\) کنید. این نمودار دوبرابر حد معمول چرخه می سازد.
   
   
3. انتقال به سمت چپ یا راست را تعیین کنید.
   در اینجا مورد دیگری داریم که نمودار دستخوش تغییری نمی شود. این معادله به جای \(C\) هیچ مقداری ندارد ـــ مقدار آن در واقع برابر با \(0\) می باشد. بنابراین این نمودار به سمت چپ یا راست منتقل نمی شود.
   
   
4. انتقال عمودی را بیابید.
   عدد \(\pi\) مقدار \(D\) می باشد. این عدد مثبت است، بنابراین این نمودار به میزان \(\pi\) واحد به سمت بالا منتقل می شود، که در حدود \(3\) واحد می باشد.
   
   
5. نمودار این تابع را از \(-2\pi\) تا \(2\pi\) ترسیم کنید، شکل 4-22 را ببینید.
   
   

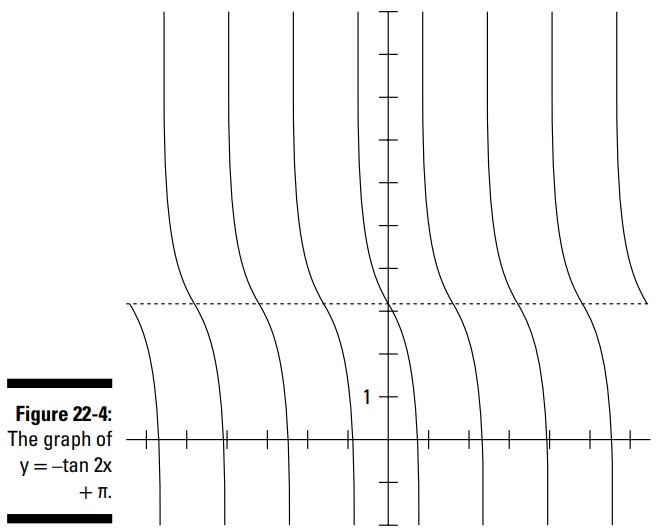
شما می توانید در شکل 4-22 ببینید که، این نمودار تابع تانژانت، هشت چرخۀ کامل را نشان می دهد. دلیل اینکه تعداد زیادی چرخه را نشان می دهد، اینست که این نمودار از \(-2\pi\) تا \(2\pi\) می رود، و طول هر چرخه تنها \(\frac{\pi}{2}\) می باشد. خط نقطه چین انتقال افقی \(\pi\) را نشان می دهد؛ من خطوط مجانب عمودی را نادیده گرفتم.