درست همان لحظه ای که با خودتان فکر می کنید این کتاب دیگر از این بهتر نمی شود، در عین حال من پیچیدگی دیگر به مثلثات اضافه می کنم. شما می توانید بسیاری از کاربردهای فیزیک و چرخه های طبیعت را با منحنی هایی که با افزودن یا تفریق دو تابع مثلثاتی بدست می آورید، یا با افزودن یک تابع مثلثاتی و مقداری توابع جبری، مدلسازی نمایید. هنگامی که توابع را با یکدیگر جمع می زنید، می توانید نمودار این جمع را با گرفتن هر مقدار \(x\) از هر تابع و یافتن جمع مقادیر \(y\) که متناظر با آن مقادیر \(x\) می باشند، بدست آورید. سپس می توانید این نقاط را با مقادیر \(x\) که مورد استفاده قرار داده اید، و مقادیر \(y\) که یافته اید، ترسیم نمایید. من چندین مثال را به شما نشان می دهم، و از آنجا که آنها خیلی زود شلوغ می شوند، من از یک ماشین حساب نموداری استفاده می کنم.





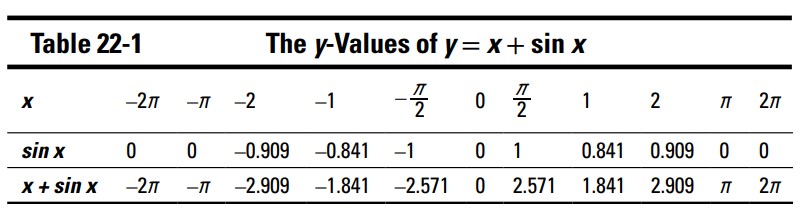
تابع \(y=x+\sin x\) مجموع تابع مثلثاتی \(y=\sin x\) و تابع جبری \(y=x\) می باشد. تابع جبریِ \(y=x\) خطی است که به صورت مورب از میان ربع صفحۀ سوم و اول می گذرد. این سینوس دارای مقادیر \(y\) می باشد که از \(-1\) تا \(1\) ، بارها و بارها تکرار می شوند. جدول 1-22 برخی از مقادیر جداگانۀ این توابع و سپس مجموع آن دو مقدار را نشان می دهد.


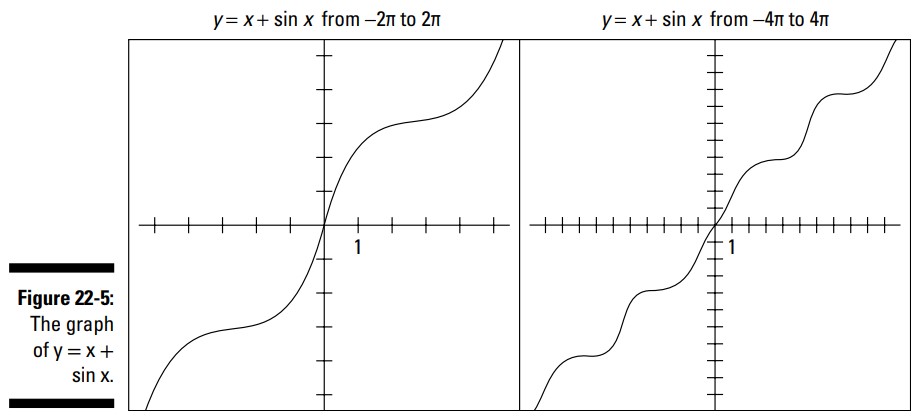
شما با مشاهدۀ این گراف می توانید درک بهتری از چگونگی کارکرد این جمع پیدا کنید. من از یک ماشین حساب نموداری برای ترسیم نمودار \(y=x+\sin x\) از \(-2\pi\) تا \(2\pi\) استفاده کرده ام. و در ادامه، برای اینکه دیدی حتی بهتر از آنچه در حال رخ دادن است، به شما بدهم، و از آنجا که گمان می کنم این منحنی شسته و رفته است، نمودار آن را از \(-4\pi\) تا \(4\pi\) در شکل 5-22 ترسیم کرده ام.


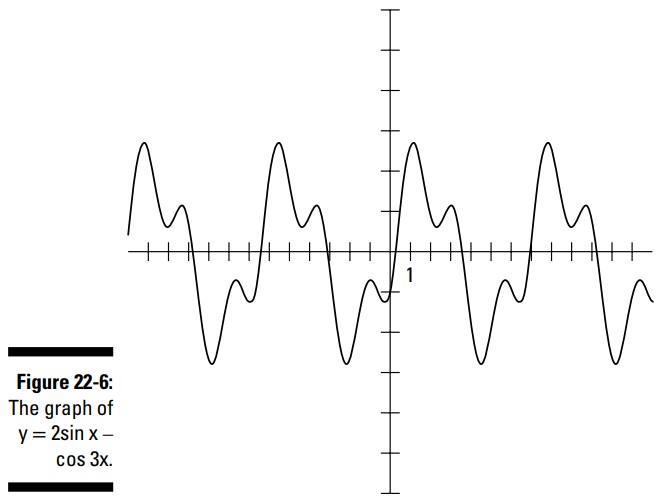
مثال بعدی به شما نشان می دهد، هنگامی که یک تابع مثلثاتی را از تابع دیگر تفریق می کنید، چه اتفاقی می تواند رخ دهد. مسلماً، من برای اینکه این نمودار را به صورت خاص جذاب سازم، مجبور بودم تا با انواع مختلف ترکیب های توابع آزمایش هایی را انجام دهم. شما نیز می توانید خودتان آزمایش های مختلفی را صورت دهید. این هم تقدیمی من به شما، نمودار \(y=2 \sin x - \cos 3x\) . من مقادیر این تابع را از یکدیگر تفریق کرده ام، یکی از دیگری، تا یک منحنی بسیار زیبا را در شکل 6-22 تولید کنم، که آن را از \(-4\pi\) تا \(4\pi\) ترسیم نموده ام.