خوب، تا اینجای کار، دانستیم که با ریاضی عادی می توانید مسالۀ شیب مستقیم را حل کنید؛ با حسابان می توانید مسالۀ شیب منحنی را حل کنید. در اینجا چندین مثال بیشتر داریم.





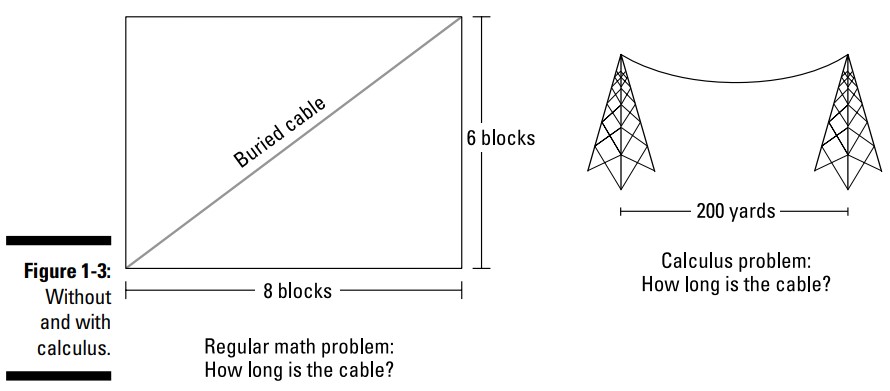
با ریاضی عادی می توانید طول یک کابل دفن شده که به صورت مورب از یک گوشۀ یک پارک تا گوشۀ دیگر آن امتداد یافته است را تعیین کنید (قضیۀ فیثاغورث را که بیاد می آورید؟). با حسابان می توانید طول یک کابل را که بین دو برج آویزان شده است، تعیین کنید که به شکل یک منحنی زنجیری (catenary) می باشد (راستی، منحنی زنجیری با یک کمان مدور ساده یا یک سهمی متفاوت می باشد). دانستن طول دقیق برای یک شرکت برق که در حال برنامه ریزی برای هزاران مایل از کابل های الکتریکی می باشد، بسیار حائز اهمیت است. شکل 3-1 را ببینید.


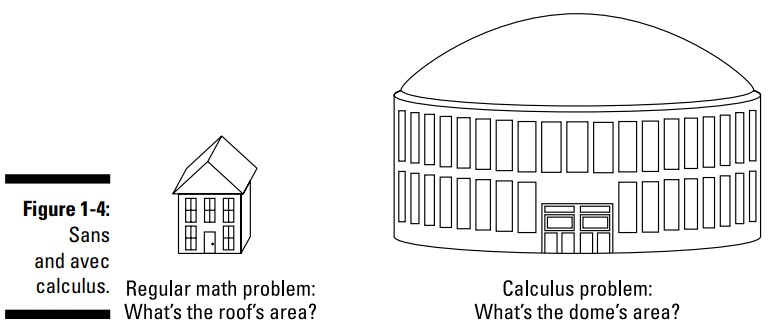
شما می توانید با هندسۀ معمولی، مساحت سقف مسطحِ یک خانه را بدست آورید. با حسابان شما می توانید مساحت یک گنبد غیرکروی شکل پیچیده، مانند ورزشگاه مترودوم میناپولیس (Minneapolis Metrodome) را تعیین کنید. معمارانی که اینگونه ساختمان ها را طراحی می کنند، نیاز به دانستن مساحت این گنبد دارند تا بتوانند بهای تمام شدۀ مصالح را تعیین کنند و همچنین وزن گنبد را (همراه با برف روی آن و بدون وجود برف روی آن) محاسبه نمایند. مسلماً، دانستن وزن برای برنامه ریزی استحکام ساختارهای نگهدارندۀ این وزن، مورد نیاز است. شکل 4-1 را ببینید.


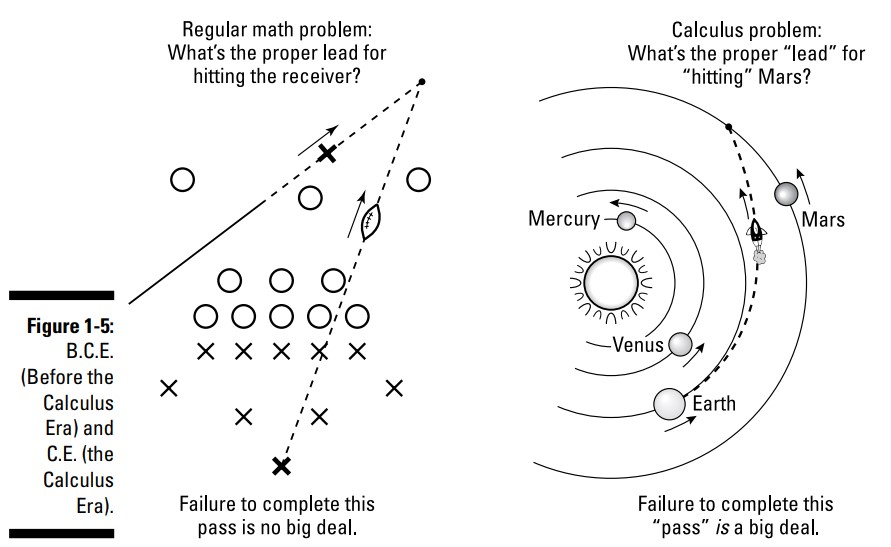
با ریاضیات عادی و اندکی فیزیک ساده، شما می توانید محاسبه کنید، یک کوارتربک (quarterback) چقدر باید گیرنده اش را هدایت کند تا بتواند یک پاس را کامل کند. (در اینجا فرض من بر اینست که آن دریافت کننده در یک خط راست و با سرعتی ثابت می دود.) اما هنگامی که ناسا (NASA)، در سال 1975 ، هدایت مورد نیاز برای پروژۀ وایکینک مارس (Viking) را پیش می برد، نیاز به حسابان داشت، زیرا هم زمین و هم مارس در مدارهای بیضوی (در شکلهای مختلف) در سفرند و سرعت هر کدام از آنها به طور مداوم تغییر می کند ـــ بدون اشاره به این واقعیت که این فضاپیما در سفرش به مارس، در طول مسیر با کشش های گرانشی مختلف ناشی از زمین، ماه، مارس، و خورشید، که به طور مدوام نیز تغییر می کنند تحت تاثیر قرار می گیرد. شکل 5-1 را ببینید.


شما در طول این کتاب کاربردهای زیادی از حسابان در دنیای واقعی را خواهید دید. مسأله های مشتق گیری (differentiation) در بخش چهارم همگی شامل تندی یک منحنی می باشند ـــ همانند تندی انحنای شیب که در شکل 1-1 نشان داده شده است. در بخش پنجم مسأله های انتگرال گیری (integration) را انجام خواهید داد، مشابه مسالۀ طول کابل که در شکل 3-1 مشاهده نمودید. این مسأله ها شامل شکستن چیزی به بخشهای کوچک، محاسبۀ هر بخش، و سپس جمع کردن این بخشها برای رسیدن به مجموع، می باشد. در فصل 2 در این باره بیشتر خواهید دانست.