خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تعریف مشتق گیری (Differentiation)

این کتاب دو مفهوم اصلی در حسابان ـــ مشتق گیری (differentiation) و انتگرال گیری (integration) ـــ را پوشش می دهد، همچنین به موضوع سومی با نام سری های نامتناهی (infinite series) در حسابان می پردازد. هر سۀ این موضوعات بر اساس قوانین معمول جبر و هندسه ساخته شده اند و همگی شامل مفهوم بی نهایت می باشند.

مشتق گیری (Differentiation) یا دیفرانسیل گیری، فرآیند یافتن مشتق (derivative) یک منحنی می باشد. و کلمۀ مشتق در واقع صرفاً یک نام فانتزی در حسابان برای اشاره به شیب یک منحنی یا تندی آن منحنی می باشد. و از آنجا که شیب یک منحنی برابر با یک نسبت ساده (مانند مایل بر ساعت یا سود در هر واحد) می باشد، مشتق نیز همانند شیب یک نسبت می باشد.
در جبر در مورد شیب یک خط چیزهایی را فرا گرفتید ـــ شیب یک خط نسبتی بین rise و run می باشد. به عبارت دیگر، \(\text{Slope}=\frac{\text{rise}}{\text{run}}\) . شکل 1-2 را ببینید.
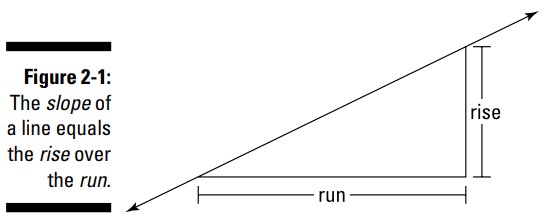
در شکل 1-2، rise برابر با نصف run می باشد، بنابراین این خط دارای شیب \(\frac{1}{2}\) می باشد.
در یک منحنی، شیب مدام تغییر می کند، بنابراین شما برای تعیین شیب منحنی نیاز به حسابان دارید. شکل 2-2 را ببینید.
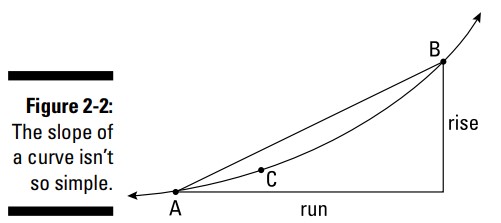
درست همانند خط موجود در شکل 1-2 ، خط راست بین \(A\) و \(B\) در شکل 2-2 دارای شیب \(\frac{1}{2}\) می باشد. و شیب این خط در هر نقطه ای بین \(A\) و \(B\) همین است. اما شما میتوانید ببینید که برخلاف این خط، شیب این منحنی بین نقاط \(A\) و \(B\) تغییر می کند. در \(A\) تندی این منحنی از تندی خط کمتر است، و در \(B\) ، منحنی از خط تندتر است. اگر شیب دقیق در نقطۀ فرضی \(C\) را بخواهید، چکار باید کنید؟ آیا می توانید آن را حدس بزنید؟ زمان حدس زدن شما به پایان رسید. پاسخ اینست: شما بزرگنمایی می کنید. شکل 3-2 را ببینید.
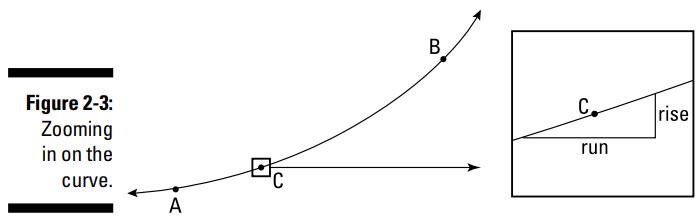
هنگامی که به اندازۀ کافی بزرگنمایی کنید ـــ واقعاً زیاد، در واقع بی نهایت زیاد ـــ این تکه کوچک از منحنی تبدیل به یک خط راست می شود، و شما می توانید شیب آن را به همان روش قدیمی بدست آورید. این چگونگی کارکرد مشتق گیری می باشد.
از آنجا که مشتق یک منحنی یک شیب است ـــ که برابر با \(\frac{\text{rise}}{\text{run}}\) است ـــ مشتق نیز یک نسبت می باشد، مانند مایل بر ساعت یا گالن در دقیقه (نام یک نسبت خاص که به سادگی بستگی به واحدهای مورد استفاده در محورهای \(x\) و \(y\) دارد). دو نمودار موجود در شکل 4-2 یک ارتباط بین مسافت و زمان را نشان می دهد ـــ آنها می توانند نشان دهندۀ یک سفر در ماشین شما باشند.
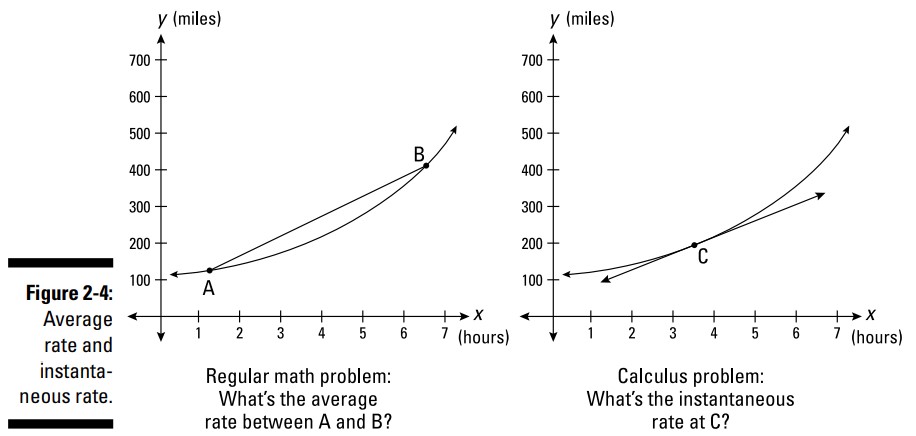
یک مسألۀ جبر معمولی در سمت چپ شکل 4-2 نشان داده شده است. اگر مختصات \(x\) و \(y\) از نقاط \(A\) و \(B\) را داشته باشید، می توانید از فرمول شیب \(\biggl( \text{Slope}=\frac{\text{rise}}{\text{run}} = \frac{y_2-y_1}{x_2-x_1} \biggr)\) برای محاسبۀ شیب بین \(A\) و \(B\) استفاده کنید، و در این مسأله، شیب به شما نرخ میانگین را در مایل بر ساعت برای بازۀ \(A\) تا \(B\) می دهد.
از سوی دیگر، برای مسالۀ سمت چپ، نیاز به حسابان دارید. (شما نمی توانید از فرمول شیب خط استفاده کنید، زیرا شما فقط یک نقطه دارید.) با استفاده از مشتق این منحنی، شما می توانید شیب دقیق یا تندی در نقطۀ \(C\) را تعیین کنید. درست در سمت چپ \(C\) بر روی منحنی، شیب اندکی کمتر است، و درست در سمت راست \(C\) بر روی منحنی، شیب اندکی بیشتر است. اما دقیقاً در \(C\)، برای یک لحظۀ بی نهایت کوچک (infinitesimal)، شما شیبی را بدست می آورید که از شیبهای همسایۀ آن متفاوت می باشد. شیب این نقطۀ واحد بی نهایت کوچک بر روی منحنی، نسبت لحظه ای (instantaneous rate) را در واحد مایل بر ساعت در نقطۀ \(C\) به شما می دهد.

معرفی مشتق گیری (دیفرانسیل گیری)
مشتق گیری (Differentiation) یا دیفرانسیل گیری، فرآیند یافتن مشتق (derivative) یک منحنی می باشد. و کلمۀ مشتق در واقع صرفاً یک نام فانتزی در حسابان برای اشاره به شیب یک منحنی یا تندی آن منحنی می باشد. و از آنجا که شیب یک منحنی برابر با یک نسبت ساده (مانند مایل بر ساعت یا سود در هر واحد) می باشد، مشتق نیز همانند شیب یک نسبت می باشد.
مشتق یک شیب است
در جبر در مورد شیب یک خط چیزهایی را فرا گرفتید ـــ شیب یک خط نسبتی بین rise و run می باشد. به عبارت دیگر، \(\text{Slope}=\frac{\text{rise}}{\text{run}}\) . شکل 1-2 را ببینید.
یادداشت مترجم: کسر مطرح شده به صورت \(\frac{\text{rise}}{\text{run}}\) بخشی از فرمول شیب نمی باشد، این صرفاً یک یاد آور برای انگلیسی زبان ها است که بدلیل وجود آن در شکلهای کتاب ما هم مطرحش کردیم تا باعث سردرگمی نگردد.

در شکل 1-2، rise برابر با نصف run می باشد، بنابراین این خط دارای شیب \(\frac{1}{2}\) می باشد.
در یک منحنی، شیب مدام تغییر می کند، بنابراین شما برای تعیین شیب منحنی نیاز به حسابان دارید. شکل 2-2 را ببینید.

درست همانند خط موجود در شکل 1-2 ، خط راست بین \(A\) و \(B\) در شکل 2-2 دارای شیب \(\frac{1}{2}\) می باشد. و شیب این خط در هر نقطه ای بین \(A\) و \(B\) همین است. اما شما میتوانید ببینید که برخلاف این خط، شیب این منحنی بین نقاط \(A\) و \(B\) تغییر می کند. در \(A\) تندی این منحنی از تندی خط کمتر است، و در \(B\) ، منحنی از خط تندتر است. اگر شیب دقیق در نقطۀ فرضی \(C\) را بخواهید، چکار باید کنید؟ آیا می توانید آن را حدس بزنید؟ زمان حدس زدن شما به پایان رسید. پاسخ اینست: شما بزرگنمایی می کنید. شکل 3-2 را ببینید.

هنگامی که به اندازۀ کافی بزرگنمایی کنید ـــ واقعاً زیاد، در واقع بی نهایت زیاد ـــ این تکه کوچک از منحنی تبدیل به یک خط راست می شود، و شما می توانید شیب آن را به همان روش قدیمی بدست آورید. این چگونگی کارکرد مشتق گیری می باشد.
مشتق یک نسبت است
از آنجا که مشتق یک منحنی یک شیب است ـــ که برابر با \(\frac{\text{rise}}{\text{run}}\) است ـــ مشتق نیز یک نسبت می باشد، مانند مایل بر ساعت یا گالن در دقیقه (نام یک نسبت خاص که به سادگی بستگی به واحدهای مورد استفاده در محورهای \(x\) و \(y\) دارد). دو نمودار موجود در شکل 4-2 یک ارتباط بین مسافت و زمان را نشان می دهد ـــ آنها می توانند نشان دهندۀ یک سفر در ماشین شما باشند.

یک مسألۀ جبر معمولی در سمت چپ شکل 4-2 نشان داده شده است. اگر مختصات \(x\) و \(y\) از نقاط \(A\) و \(B\) را داشته باشید، می توانید از فرمول شیب \(\biggl( \text{Slope}=\frac{\text{rise}}{\text{run}} = \frac{y_2-y_1}{x_2-x_1} \biggr)\) برای محاسبۀ شیب بین \(A\) و \(B\) استفاده کنید، و در این مسأله، شیب به شما نرخ میانگین را در مایل بر ساعت برای بازۀ \(A\) تا \(B\) می دهد.
از سوی دیگر، برای مسالۀ سمت چپ، نیاز به حسابان دارید. (شما نمی توانید از فرمول شیب خط استفاده کنید، زیرا شما فقط یک نقطه دارید.) با استفاده از مشتق این منحنی، شما می توانید شیب دقیق یا تندی در نقطۀ \(C\) را تعیین کنید. درست در سمت چپ \(C\) بر روی منحنی، شیب اندکی کمتر است، و درست در سمت راست \(C\) بر روی منحنی، شیب اندکی بیشتر است. اما دقیقاً در \(C\)، برای یک لحظۀ بی نهایت کوچک (infinitesimal)، شما شیبی را بدست می آورید که از شیبهای همسایۀ آن متفاوت می باشد. شیب این نقطۀ واحد بی نهایت کوچک بر روی منحنی، نسبت لحظه ای (instantaneous rate) را در واحد مایل بر ساعت در نقطۀ \(C\) به شما می دهد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: