ریشه ها و به ویژه جذرها، همیشه در حسابان ظاهر می شوند. بنابراین دانستن چگونگی کارکرد آنها و درک ارتباطات بنیادی بین ریشه ها و توانها ضروری است. و البته، این همان چیزی است که قصد گفتنش را دارم.

قوانین ریشه ها

هر ریشه ای می تواند به یک توان تبدیل گردد، به عنوان مثال:
$$
\sqrt[3]{x} = x^{\frac{1}{3}} \\
\sqrt{x}=x^{\frac{1}{2}} \\
\sqrt[4]{x^3}=x^{\frac{3}{4}}
$$
بنابراین، اگر مسأله ای دارای ریشه ها داشتید، می توانید هر ریشه را به یک توان تبدیل کنید و از قوانین توانها برای حل کردن آن مسأله استفاده کنید (این یک تکنیک بسیار مفید است). از آنجا که این گزینه را در اختیار دارید، قوانین ریشه ها که در ادامه آمده اند نسبت به قوانین توانها، حائز اهمیت کمتری می باشند، اما به هر حال شما باید آنها را بدانید:

• \(\sqrt{0} = 0\) و \(\sqrt{1}=1\)
  
  هیچ عدد منفی نمی تواند زیر ریشۀ زوج قرار بگیرد. شما نمی توانید عددی منفی را زیر یک جذر (ریشۀ دوم) یا زیر هر ریشۀ زوج دیگری داشته باشید ـــ دست کم نه در حسابان ساده.
  
  
• \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\) ، \(\sqrt[3]{a} \cdot \sqrt[3]{b}=\sqrt[3]{ab}\)، و \(\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{ab}\)
  
  
• \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)، \(\frac{\sqrt[3]{a}}{\sqrt[3]{b}} = \sqrt[3]{\frac{a}{b}}\)، و \(\frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}\)
  
  
• \(\sqrt[3]{\sqrt[4]{a}} = \sqrt[12]{a}\) و \(\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}\)
  شما ایندکس ریشه ها را در یکدیگر ضرب می کنید.
  
  
• \(\sqrt{a^2}=|a|\) ، \(\sqrt[4]{a^4}=|a|\)، \(\sqrt[6]{a^6}=|a|\)، و به همین ترتیب.
  اگر یک ریشۀ زوج داشته باشید، در پاسخ نیاز به علامت قدرمطلق دارید، زیرا \(a\) چه مثبت و چه منفی باشد، پاسخ مثبت است. اگر ریشه عددی فرد باشد، نیازی به علامت قدرمطلق ندارید.
  
  
• \(\sqrt[3]{a^3} = a\)، \(\sqrt[5]{a^5}=a\)، و به همین ترتیب.
  
  
• \(\sqrt{a^2+b^2}=a+b\) صحیح نمی باشد!
  اگر این اشتباه را بکنید مستقیم به زندان می روید. سعی کنید آن را با اعداد حل کنید: \(\sqrt{2^2+3^2}=\sqrt{13}\) ، که با \(2+3\) برابر نمی باشد.
  

ساده سازی ریشه ها

در اینجا دو چیز دیگر در مورد ریشه ها داریم. ابتدا، نیاز به دانستن دو روش برای ساده سازی ریشه هایی همچون \(\sqrt{300}\) یا \(\sqrt{504}\) دارید.

روش سریع در مورد \(\sqrt{300}\) جواب می دهد، زیرا به آسانی می توانید یک مربع کامل، یعنی \(100\)، را ببینید، که \(300\) بر آن بخش پذیر می باشد. از آنجا که \(300\) برابر با \(100\) ضربدر \(3\) می باشد، \(100\) را به شکل جذر آن یعنی \(10\) می نویسید و \(3\) را درون جذر باقی می گذارید. پاسخ برابر با \(10\sqrt{3}\) می باشد.

در مورد \(\sqrt{504}\)، یافتن یک مربع کامل بزرگ که \(504\) بر آن بخش پذیر باشد، ساده نیست، بنابراین شما نیاز به استفاده از روش طولانی تری دارید:

1. عدد \(504\) را به حاصلضرب تمامی فاکتورهای اول (prime factors) آن بشکنید. $$\sqrt{504}=\sqrt{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 7}$$
   
2. دور هر جفت از اعداد یک دایره بکشید.
   
   
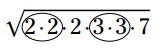
3. به ازاء هر جفت دایره دار، یک عدد را بیرون بکشید. $$2 \cdot 3 \sqrt{2 \cdot 7}$$
   
4. عبارت را ساده کنید. $$6\sqrt{14}$$
   

آخرین چیز در مورد ریشه ها اینست که بنا به یک قرارداد، شما یک ریشه را در مخرج یک کسر رها نمی سازید ـــ این یک قرارداد احمقانه و بی مورد است، اما هنوز هم تدریس می شود، بنابراین در اینجا آن را داریم. به عنوان مثال، اگر پاسخ شما \(\frac{2}{\sqrt{3}}\) باشد، شما آن را در \(\frac{\sqrt{3}}{\sqrt{3}}\) ضرب می کنید:
$$\frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{2\sqrt{3}}{3}$$